An efficient nonconvex reformulation of stagewise convex optimization problems

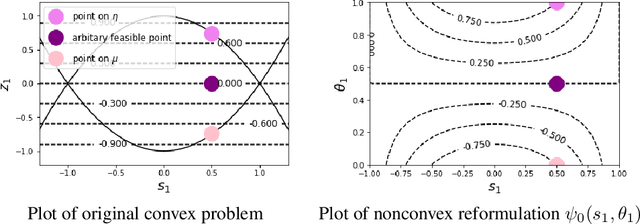
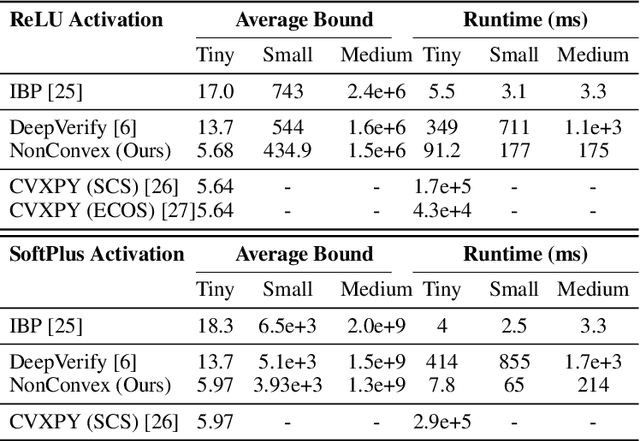
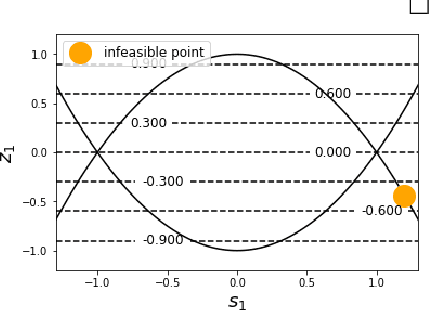
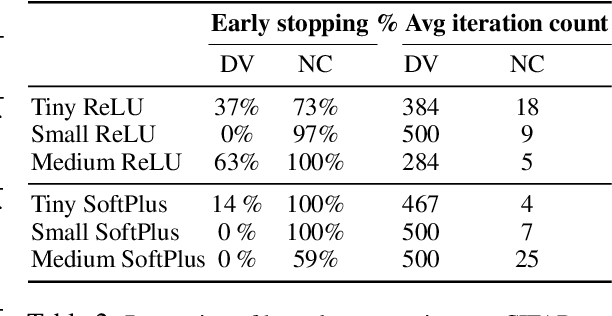
Convex optimization problems with staged structure appear in several contexts, including optimal control, verification of deep neural networks, and isotonic regression. Off-the-shelf solvers can solve these problems but may scale poorly. We develop a nonconvex reformulation designed to exploit this staged structure. Our reformulation has only simple bound constraints, enabling solution via projected gradient methods and their accelerated variants. The method automatically generates a sequence of primal and dual feasible solutions to the original convex problem, making optimality certification easy. We establish theoretical properties of the nonconvex formulation, showing that it is (almost) free of spurious local minima and has the same global optimum as the convex problem. We modify PGD to avoid spurious local minimizers so it always converges to the global minimizer. For neural network verification, our approach obtains small duality gaps in only a few gradient steps. Consequently, it can quickly solve large-scale verification problems faster than both off-the-shelf and specialized solvers.

Contrastive Training for Improved Out-of-Distribution Detection

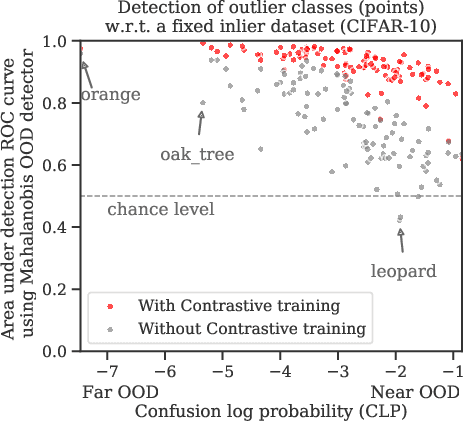
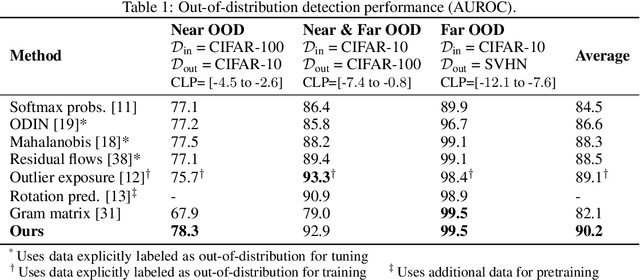
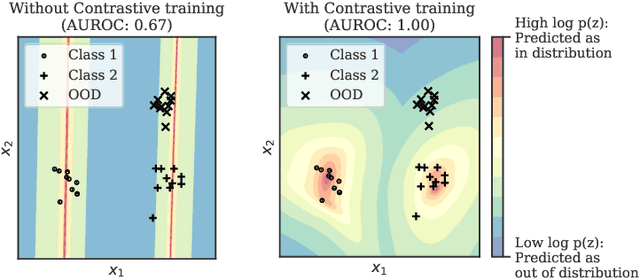
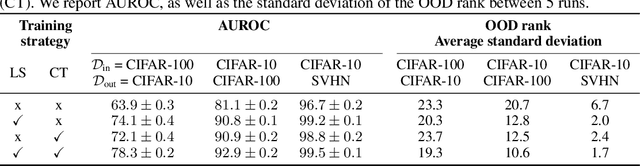
Reliable detection of out-of-distribution (OOD) inputs is increasingly understood to be a precondition for deployment of machine learning systems. This paper proposes and investigates the use of contrastive training to boost OOD detection performance. Unlike leading methods for OOD detection, our approach does not require access to examples labeled explicitly as OOD, which can be difficult to collect in practice. We show in extensive experiments that contrastive training significantly helps OOD detection performance on a number of common benchmarks. By introducing and employing the Confusion Log Probability (CLP) score, which quantifies the difficulty of the OOD detection task by capturing the similarity of inlier and outlier datasets, we show that our method especially improves performance in the `near OOD' classes -- a particularly challenging setting for previous methods.

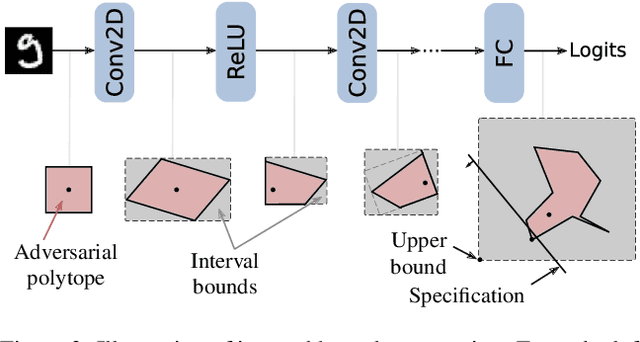
Lagrangian Decomposition for Neural Network Verification

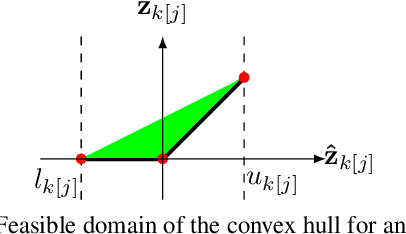
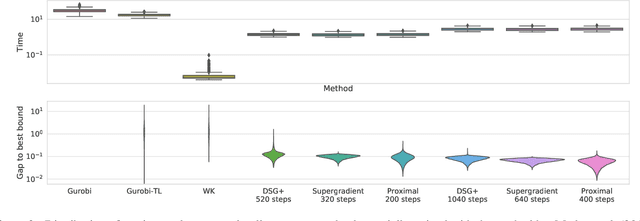
A fundamental component of neural network verification is the computation of bounds on the values their outputs can take. Previous methods have either used off-the-shelf solvers, discarding the problem structure, or relaxed the problem even further, making the bounds unnecessarily loose. We propose a novel approach based on Lagrangian Decomposition. Our formulation admits an efficient supergradient ascent algorithm, as well as an improved proximal algorithm. Both the algorithms offer three advantages: (i) they yield bounds that are provably at least as tight as previous dual algorithms relying on Lagrangian relaxations; (ii) they are based on operations analogous to forward/backward pass of neural networks layers and are therefore easily parallelizable, amenable to GPU implementation and able to take advantage of the convolutional structure of problems; and (iii) they allow for anytime stopping while still providing valid bounds. Empirically, we show that we obtain bounds comparable with off-the-shelf solvers in a fraction of their running time, and obtain tighter bounds in the same time as previous dual algorithms. This results in an overall speed-up when employing the bounds for formal verification.

Branch and Bound for Piecewise Linear Neural Network Verification

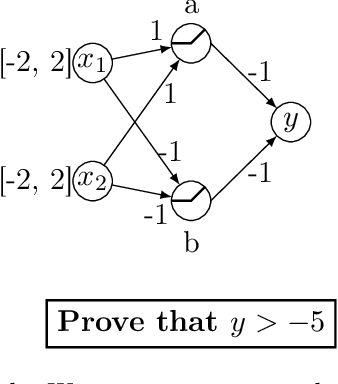
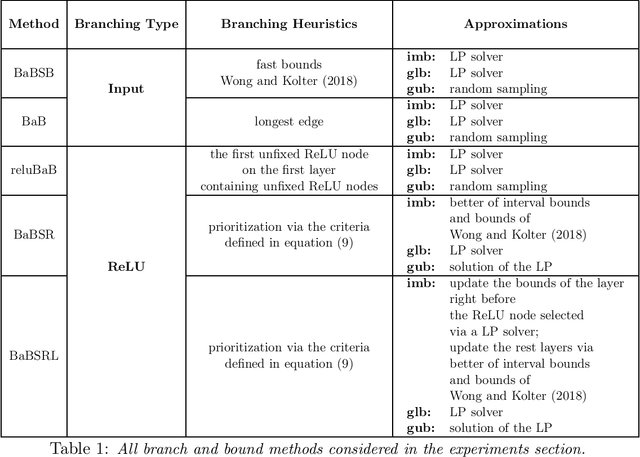
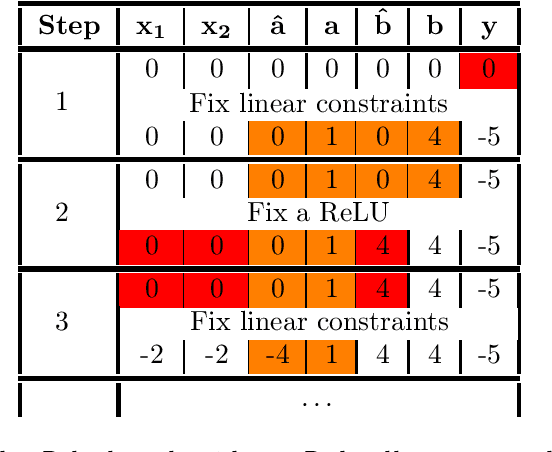
The success of Deep Learning and its potential use in many safety-critical applications has motivated research on formal verification of Neural Network (NN) models. In this context, verification means verifying whether a NN model satisfies certain input-output properties. Despite the reputation of learned NN models as black boxes, and the theoretical hardness of proving useful properties about them, researchers have been successful in verifying some classes of models by exploiting their piecewise linear structure and taking insights from formal methods such as Satisifiability Modulo Theory. However, these methods are still far from scaling to realistic neural networks. To facilitate progress on this crucial area, we make two key contributions. First, we present a unified framework based on branch and bound that encompasses previous methods. This analysis results in the identification of new methods that combine the strengths of multiple existing approaches, accomplishing a speedup of two orders of magnitude compared to the previous state of the art. Second, we propose a new data set of benchmarks which includes a collection of previously released test cases. We use the benchmark to provide a thorough experimental comparison of existing algorithms and identify the factors impacting the hardness of verification problems.

Knowing When to Stop: Evaluation and Verification of Conformity to Output-size Specifications

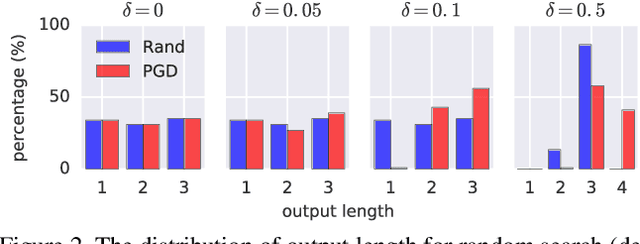
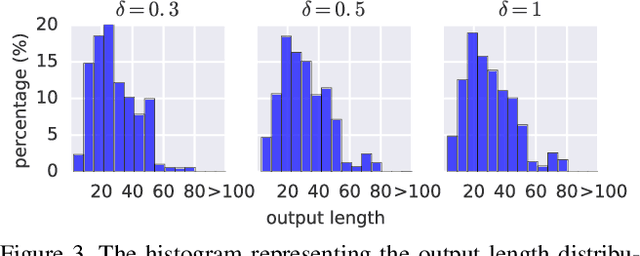
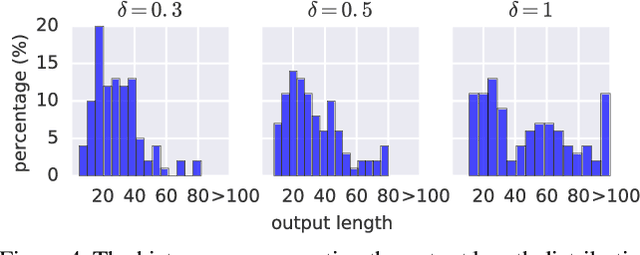
Models such as Sequence-to-Sequence and Image-to-Sequence are widely used in real world applications. While the ability of these neural architectures to produce variable-length outputs makes them extremely effective for problems like Machine Translation and Image Captioning, it also leaves them vulnerable to failures of the form where the model produces outputs of undesirable length. This behavior can have severe consequences such as usage of increased computation and induce faults in downstream modules that expect outputs of a certain length. Motivated by the need to have a better understanding of the failures of these models, this paper proposes and studies the novel output-size modulation problem and makes two key technical contributions. First, to evaluate model robustness, we develop an easy-to-compute differentiable proxy objective that can be used with gradient-based algorithms to find output-lengthening inputs. Second and more importantly, we develop a verification approach that can formally verify whether a network always produces outputs within a certain length. Experimental results on Machine Translation and Image Captioning show that our output-lengthening approach can produce outputs that are 50 times longer than the input, while our verification approach can, given a model and input domain, prove that the output length is below a certain size.

Verification of Non-Linear Specifications for Neural Networks

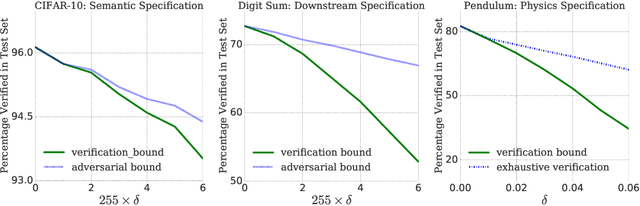
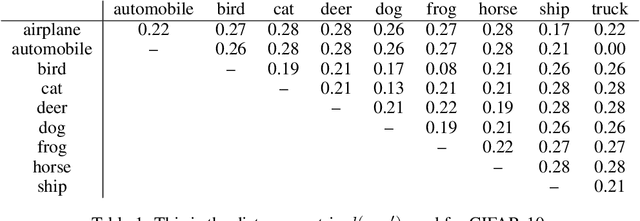
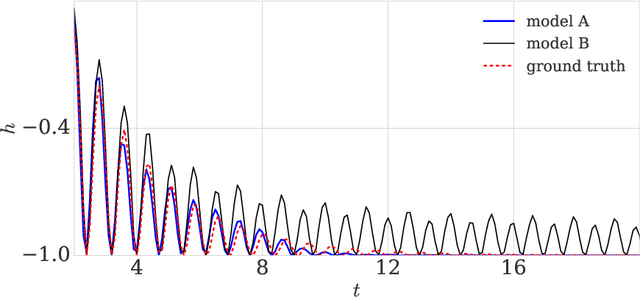
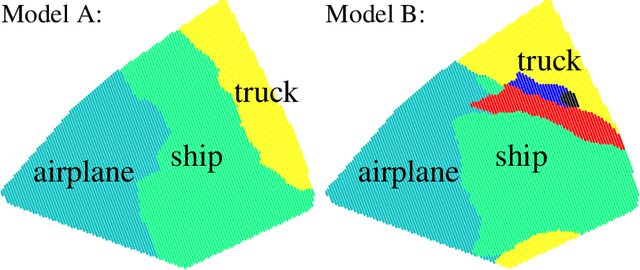
Prior work on neural network verification has focused on specifications that are linear functions of the output of the network, e.g., invariance of the classifier output under adversarial perturbations of the input. In this paper, we extend verification algorithms to be able to certify richer properties of neural networks. To do this we introduce the class of convex-relaxable specifications, which constitute nonlinear specifications that can be verified using a convex relaxation. We show that a number of important properties of interest can be modeled within this class, including conservation of energy in a learned dynamics model of a physical system; semantic consistency of a classifier's output labels under adversarial perturbations and bounding errors in a system that predicts the summation of handwritten digits. Our experimental evaluation shows that our method is able to effectively verify these specifications. Moreover, our evaluation exposes the failure modes in models which cannot be verified to satisfy these specifications. Thus, emphasizing the importance of training models not just to fit training data but also to be consistent with specifications.

On the Effectiveness of Interval Bound Propagation for Training Verifiably Robust Models

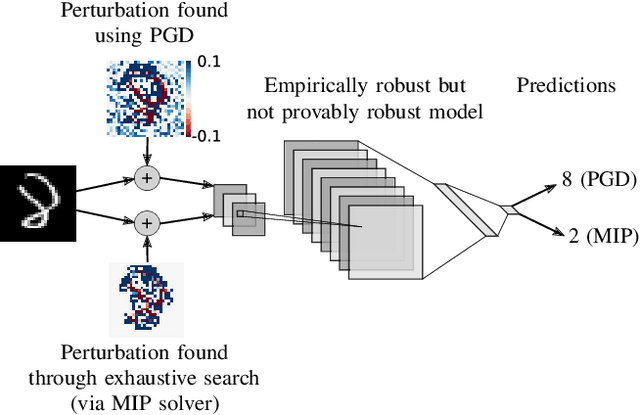
Recent works have shown that it is possible to train models that are verifiably robust to norm-bounded adversarial perturbations. While these recent methods show promise, they remain hard to scale and difficult to tune. This paper investigates how interval bound propagation (IBP) using simple interval arithmetic can be exploited to train verifiably robust neural networks that are surprisingly effective. While IBP itself has been studied in prior work, our contribution is in showing that, with an appropriate loss and careful tuning of hyper-parameters, verified training with IBP leads to a fast and stable learning algorithm. We compare our approach with recent techniques, and train classifiers that improve on the state-of-the-art in single-model adversarial robustness: we reduce the verified error rate from 3.67% to 2.23% on MNIST (with $\ell_\infty$ perturbations of $\epsilon = 0.1$), from 19.32% to 8.05% on MNIST (at $\epsilon = 0.3$), and from 78.22% to 72.91% on CIFAR-10 (at $\epsilon = 8/255$).

Efficient Relaxations for Dense CRFs with Sparse Higher Order Potentials

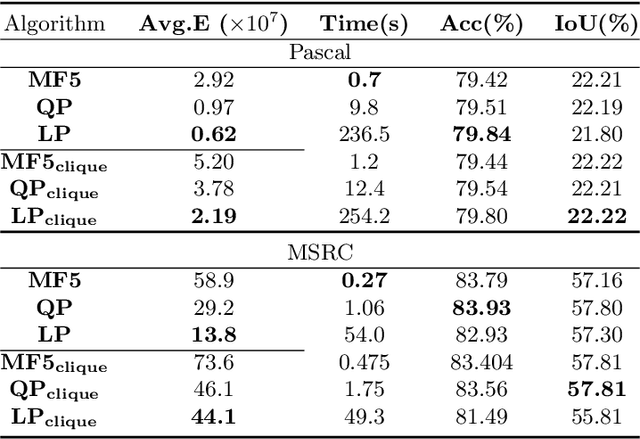
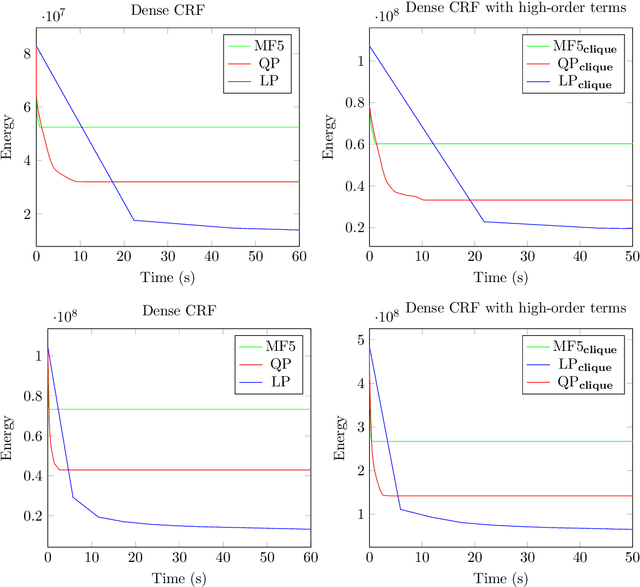
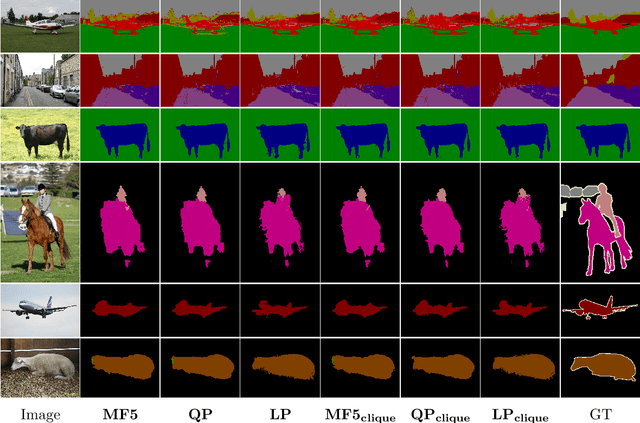
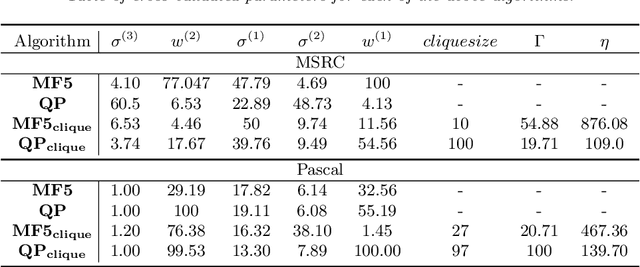
Dense conditional random fields (CRFs) have become a popular framework for modelling several problems in computer vision such as stereo correspondence and multi-class semantic segmentation. By modelling long-range interactions, dense CRFs provide a labelling that captures finer detail than their sparse counterparts. Currently, the state-of-the-art algorithm performs mean-field inference using a filter-based method but fails to provide a strong theoretical guarantee on the quality of the solution. A question naturally arises as to whether it is possible to obtain a maximum a posteriori (MAP) estimate of a dense CRF using a principled method. Within this paper, we show that this is indeed possible. We will show that, by using a filter-based method, continuous relaxations of the MAP problem can be optimised efficiently using state-of-the-art algorithms. Specifically, we will solve a quadratic programming (QP) relaxation using the Frank-Wolfe algorithm and a linear programming (LP) relaxation by developing a proximal minimisation framework. By exploiting labelling consistency in the higher-order potentials and utilising the filter-based method, we are able to formulate the above algorithms such that each iteration has a complexity linear in the number of classes and random variables. The presented algorithms can be applied to any labelling problem using a dense CRF with sparse higher-order potentials. In this paper, we use semantic segmentation as an example application as it demonstrates the ability of the algorithm to scale to dense CRFs with large dimensions. We perform experiments on the Pascal dataset to indicate that the presented algorithms are able to attain lower energies than the mean-field inference method.

A Unified View of Piecewise Linear Neural Network Verification

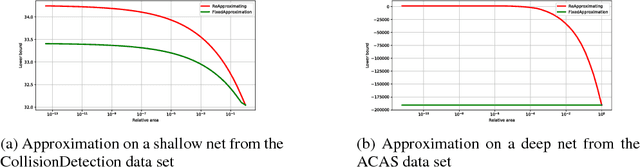
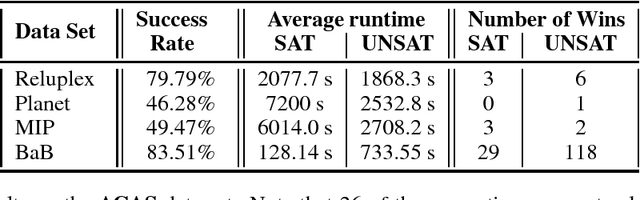
The success of Deep Learning and its potential use in many safety-critical applications has motivated research on formal verification of Neural Network (NN) models. Despite the reputation of learned NN models to behave as black boxes and the theoretical hardness of proving their properties, researchers have been successful in verifying some classes of models by exploiting their piecewise linear structure and taking insights from formal methods such as Satisifiability Modulo Theory. These methods are however still far from scaling to realistic neural networks. To facilitate progress on this crucial area, we make two key contributions. First, we present a unified framework that encompasses previous methods. This analysis results in the identification of new methods that combine the strengths of multiple existing approaches, accomplishing a speedup of two orders of magnitude compared to the previous state of the art. Second, we propose a new data set of benchmarks which includes a collection of previously released testcases. We use the benchmark to provide the first experimental comparison of existing algorithms and identify the factors impacting the hardness of verification problems.

Leveraging Grammar and Reinforcement Learning for Neural Program Synthesis

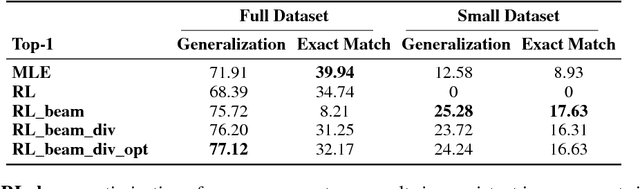
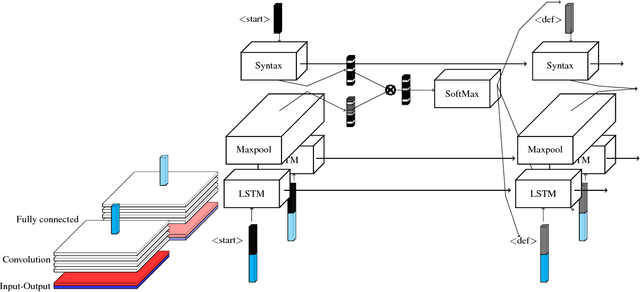
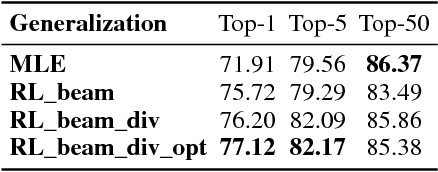
Program synthesis is the task of automatically generating a program consistent with a specification. Recent years have seen proposal of a number of neural approaches for program synthesis, many of which adopt a sequence generation paradigm similar to neural machine translation, in which sequence-to-sequence models are trained to maximize the likelihood of known reference programs. While achieving impressive results, this strategy has two key limitations. First, it ignores Program Aliasing: the fact that many different programs may satisfy a given specification (especially with incomplete specifications such as a few input-output examples). By maximizing the likelihood of only a single reference program, it penalizes many semantically correct programs, which can adversely affect the synthesizer performance. Second, this strategy overlooks the fact that programs have a strict syntax that can be efficiently checked. To address the first limitation, we perform reinforcement learning on top of a supervised model with an objective that explicitly maximizes the likelihood of generating semantically correct programs. For addressing the second limitation, we introduce a training procedure that directly maximizes the probability of generating syntactically correct programs that fulfill the specification. We show that our contributions lead to improved accuracy of the models, especially in cases where the training data is limited.