Differentially-Private Hierarchical Clustering with Provable Approximation Guarantees

Hierarchical Clustering is a popular unsupervised machine learning method with decades of history and numerous applications. We initiate the study of differentially private approximation algorithms for hierarchical clustering under the rigorous framework introduced by (Dasgupta, 2016). We show strong lower bounds for the problem: that any $\epsilon$-DP algorithm must exhibit $O(|V|^2/ \epsilon)$-additive error for an input dataset $V$. Then, we exhibit a polynomial-time approximation algorithm with $O(|V|^{2.5}/ \epsilon)$-additive error, and an exponential-time algorithm that meets the lower bound. To overcome the lower bound, we focus on the stochastic block model, a popular model of graphs, and, with a separation assumption on the blocks, propose a private $1+o(1)$ approximation algorithm which also recovers the blocks exactly. Finally, we perform an empirical study of our algorithms and validate their performance.

Private estimation algorithms for stochastic block models and mixture models

We introduce general tools for designing efficient private estimation algorithms, in the high-dimensional settings, whose statistical guarantees almost match those of the best known non-private algorithms. To illustrate our techniques, we consider two problems: recovery of stochastic block models and learning mixtures of spherical Gaussians. For the former, we present the first efficient $(\epsilon, \delta)$-differentially private algorithm for both weak recovery and exact recovery. Previously known algorithms achieving comparable guarantees required quasi-polynomial time. For the latter, we design an $(\epsilon, \delta)$-differentially private algorithm that recovers the centers of the $k$-mixture when the minimum separation is at least $ O(k^{1/t}\sqrt{t})$. For all choices of $t$, this algorithm requires sample complexity $n\geq k^{O(1)}d^{O(t)}$ and time complexity $(nd)^{O(t)}$. Prior work required minimum separation at least $O(\sqrt{k})$ as well as an explicit upper bound on the Euclidean norm of the centers.

Privacy Amplification Via Bernoulli Sampling

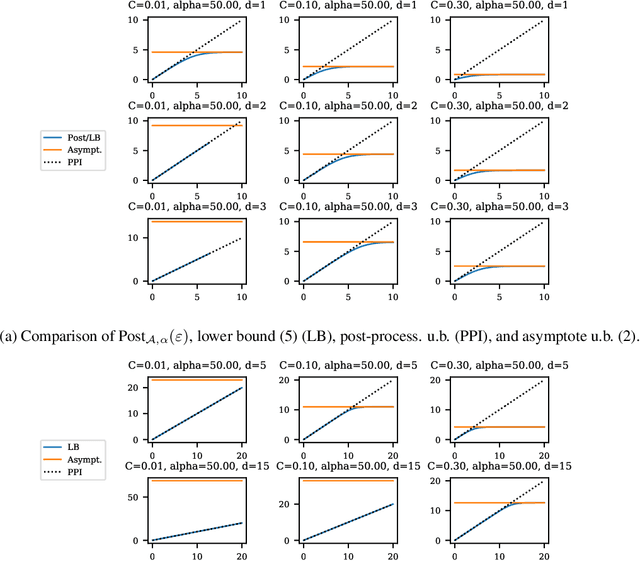
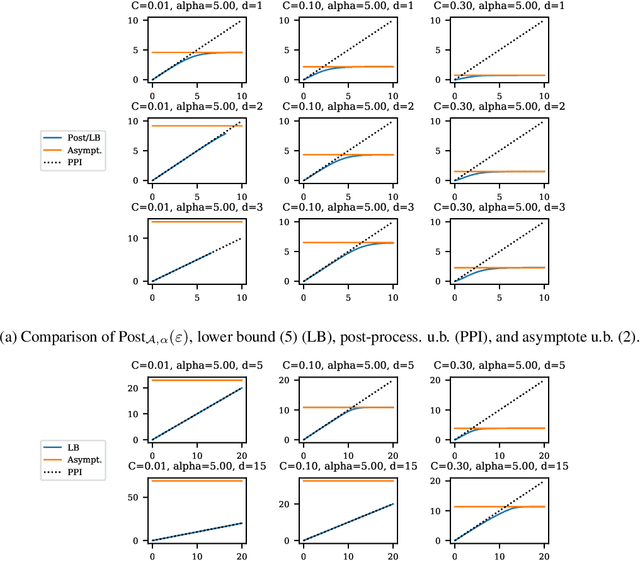
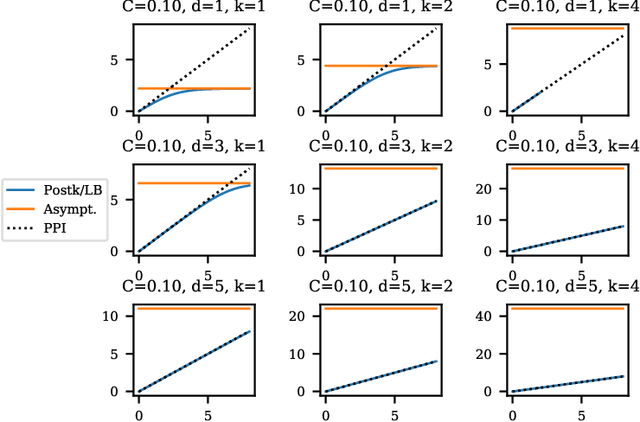
Balancing privacy and accuracy is a major challenge in designing differentially private machine learning algorithms. To improve this tradeoff, prior work has looked at privacy amplification methods which analyze how common training operations such as iteration and subsampling the data can lead to higher privacy. In this paper, we analyze privacy amplification properties of a new operation, sampling from the posterior, that is used in Bayesian inference. In particular, we look at Bernoulli sampling from a posterior that is described by a differentially private parameter. We provide an algorithm to compute the amplification factor in this setting, and establish upper and lower bounds on this factor. Finally, we look at what happens when we draw k posterior samples instead of one.

No-Substitution $k$-means Clustering with Low Center Complexity and Memory

Clustering is a fundamental task in machine learning. Given a dataset $X = \{x_1, \ldots x_n\}$, the goal of $k$-means clustering is to pick $k$ "centers" from $X$ in a way that minimizes the sum of squared distances from each point to its nearest center. We consider $k$-means clustering in the online, no substitution setting, where one must decide whether to take $x_t$ as a center immediately upon streaming it and cannot remove centers once taken. The online, no substitution setting is challenging for clustering--one can show that there exist datasets $X$ for which any $O(1)$-approximation $k$-means algorithm must have center complexity $\Omega(n)$, meaning that it takes $\Omega(n)$ centers in expectation. Bhattacharjee and Moshkovitz (2020) refined this bound by defining a complexity measure called $Lower_{\alpha, k}(X)$, and proving that any $\alpha$-approximation algorithm must have center complexity $\Omega(Lower_{\alpha, k}(X))$. They then complemented their lower bound by giving a $O(k^3)$-approximation algorithm with center complexity $\tilde{O}(k^2Lower_{k^3, k}(X))$, thus showing that their parameter is a tight measure of required center complexity. However, a major drawback of their algorithm is its memory requirement, which is $O(n)$. This makes the algorithm impractical for very large datasets. In this work, we strictly improve upon their algorithm on all three fronts; we develop a $36$-approximation algorithm with center complexity $\tilde{O}(kLower_{36, k}(X))$ that uses only $O(k)$ additional memory. In addition to having nearly optimal memory, this algorithm is the first known algorithm with center complexity bounded by $Lower_{36, k}(X)$ that is a true $O(1)$-approximation with its approximation factor being independent of $k$ or $n$.

Capacity Bounded Differential Privacy

Differential privacy, a notion of algorithmic stability, is a gold standard for measuring the additional risk an algorithm's output poses to the privacy of a single record in the dataset. Differential privacy is defined as the distance between the output distribution of an algorithm on neighboring datasets that differ in one entry. In this work, we present a novel relaxation of differential privacy, capacity bounded differential privacy, where the adversary that distinguishes output distributions is assumed to be capacity-bounded -- i.e. bounded not in computational power, but in terms of the function class from which their attack algorithm is drawn. We model adversaries in terms of restricted f-divergences between probability distributions, and study properties of the definition and algorithms that satisfy them.