Graph-based Complexity for Causal Effect by Empirical Plug-in

This paper focuses on the computational complexity of computing empirical plug-in estimates for causal effect queries. Given a causal graph and observational data, any identifiable causal query can be estimated from an expression over the observed variables, called the estimand. The estimand can then be evaluated by plugging in probabilities computed empirically from data. In contrast to conventional wisdom, which assumes that high dimensional probabilistic functions will lead to exponential evaluation time of the estimand. We show that computation can be done efficiently, potentially in time linear in the data size, depending on the estimand's hypergraph. In particular, we show that both the treewidth and hypertree width of the estimand's structure bound the evaluation complexity of the plug-in estimands, analogous to their role in the complexity of probabilistic inference in graphical models. Often, the hypertree width provides a more effective bound, since the empirical distributions are sparse.

Estimating Causal Effects from Learned Causal Networks

The standard approach to answering an identifiable causal-effect query (e.g., $P(Y|do(X)$) when given a causal diagram and observational data is to first generate an estimand, or probabilistic expression over the observable variables, which is then evaluated using the observational data. In this paper, we propose an alternative paradigm for answering causal-effect queries over discrete observable variables. We propose to instead learn the causal Bayesian network and its confounding latent variables directly from the observational data. Then, efficient probabilistic graphical model (PGM) algorithms can be applied to the learned model to answer queries. Perhaps surprisingly, we show that this \emph{model completion} learning approach can be more effective than estimand approaches, particularly for larger models in which the estimand expressions become computationally difficult. We illustrate our method's potential using a benchmark collection of Bayesian networks and synthetically generated causal models.

Boosting AND/OR-Based Computational Protein Design: Dynamic Heuristics and Generalizable UFO

Scientific computing has experienced a surge empowered by advancements in technologies such as neural networks. However, certain important tasks are less amenable to these technologies, benefiting from innovations to traditional inference schemes. One such task is protein re-design. Recently a new re-design algorithm, AOBB-K*, was introduced and was competitive with state-of-the-art BBK* on small protein re-design problems. However, AOBB-K* did not scale well. In this work we focus on scaling up AOBB-K* and introduce three new versions: AOBB-K*-b (boosted), AOBB-K*-DH (with dynamic heuristics), and AOBB-K*-UFO (with underflow optimization) that significantly enhance scalability.

Accelerating Exact and Approximate Inference for (Distributed) Discrete Optimization with GPUs

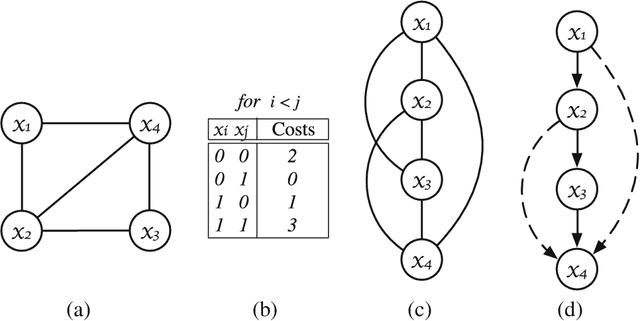
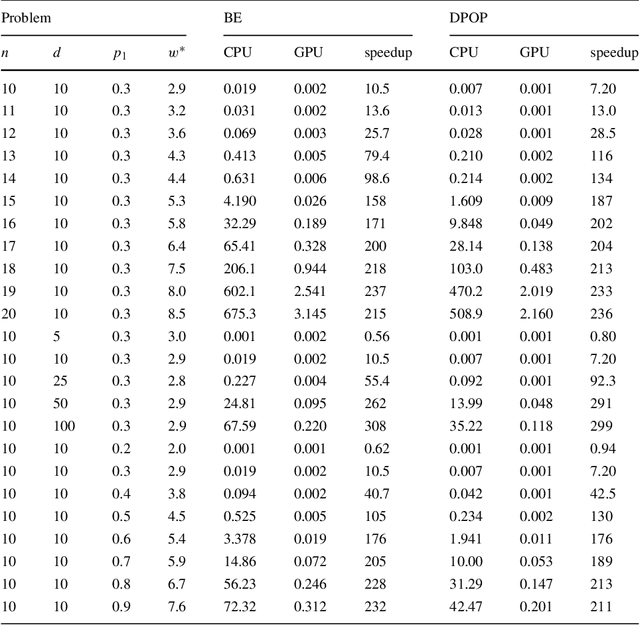
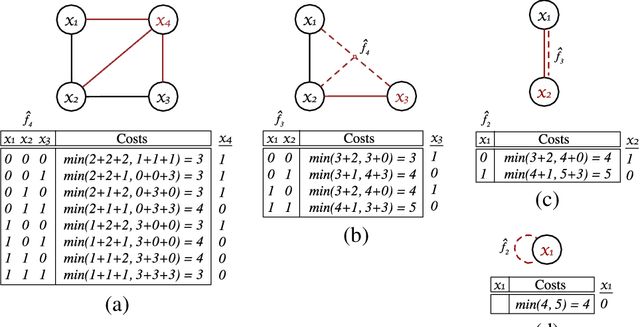
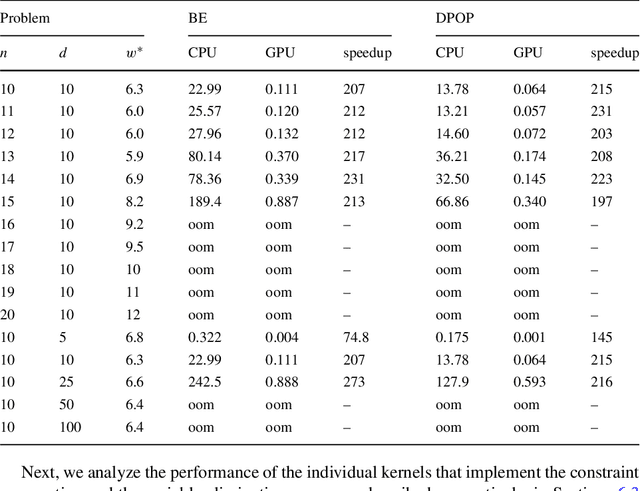
Discrete optimization is a central problem in artificial intelligence. The optimization of the aggregated cost of a network of cost functions arises in a variety of problems including (W)CSP, DCOP, as well as optimization in stochastic variants such as the tasks of finding the most probable explanation (MPE) in belief networks. Inference-based algorithms are powerful techniques for solving discrete optimization problems, which can be used independently or in combination with other techniques. However, their applicability is often limited by their compute intensive nature and their space requirements. This paper proposes the design and implementation of a novel inference-based technique, which exploits modern massively parallel architectures, such as those found in Graphical Processing Units (GPUs), to speed up the resolution of exact and approximated inference-based algorithms for discrete optimization. The paper studies the proposed algorithm in both centralized and distributed optimization contexts. The paper demonstrates that the use of GPUs provides significant advantages in terms of runtime and scalability, achieving up to two orders of magnitude in speedups and showing a considerable reduction in execution time (up to 345 times faster) with respect to a sequential version.

Probabilistic Inference Modulo Theories

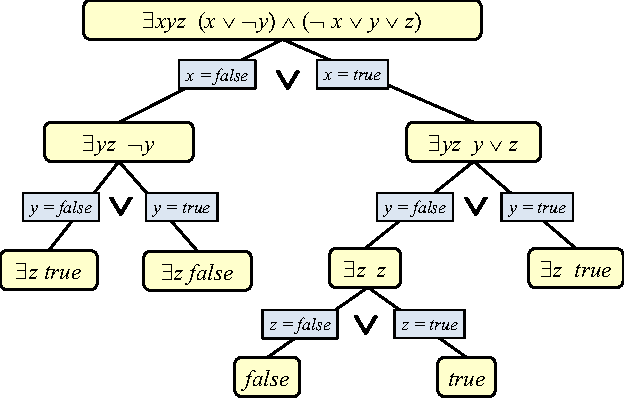
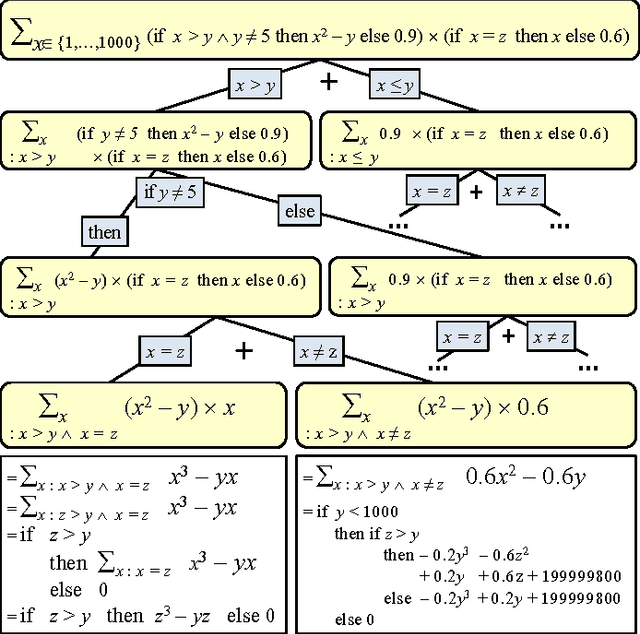
We present SGDPLL(T), an algorithm that solves (among many other problems) probabilistic inference modulo theories, that is, inference problems over probabilistic models defined via a logic theory provided as a parameter (currently, propositional, equalities on discrete sorts, and inequalities, more specifically difference arithmetic, on bounded integers). While many solutions to probabilistic inference over logic representations have been proposed, SGDPLL(T) is simultaneously (1) lifted, (2) exact and (3) modulo theories, that is, parameterized by a background logic theory. This offers a foundation for extending it to rich logic languages such as data structures and relational data. By lifted, we mean algorithms with constant complexity in the domain size (the number of values that variables can take). We also detail a solver for summations with difference arithmetic and show experimental results from a scenario in which SGDPLL(T) is much faster than a state-of-the-art probabilistic solver.

Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence (2006)

This is the Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence, which was held in Cambridge, MA, July 13 - 16 2006.

Active Tuples-based Scheme for Bounding Posterior Beliefs

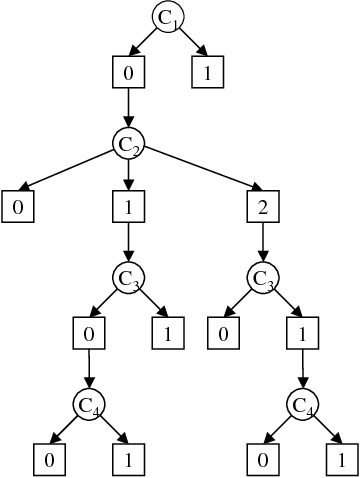
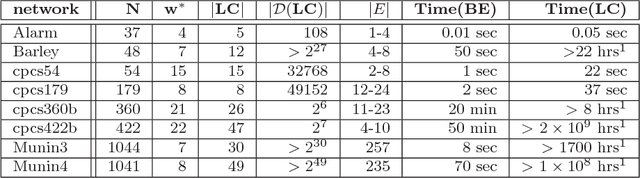
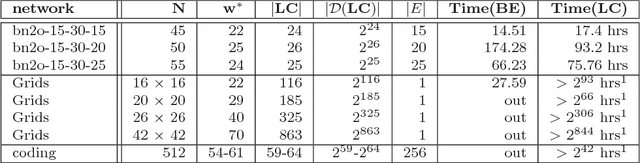
The paper presents a scheme for computing lower and upper bounds on the posterior marginals in Bayesian networks with discrete variables. Its power lies in its ability to use any available scheme that bounds the probability of evidence or posterior marginals and enhance its performance in an anytime manner. The scheme uses the cutset conditioning principle to tighten existing bounding schemes and to facilitate anytime behavior, utilizing a fixed number of cutset tuples. The accuracy of the bounds improves as the number of used cutset tuples increases and so does the computation time. We demonstrate empirically the value of our scheme for bounding posterior marginals and probability of evidence using a variant of the bound propagation algorithm as a plug-in scheme.

Join-Graph Propagation Algorithms

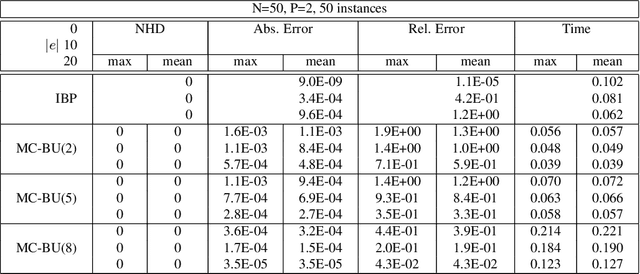
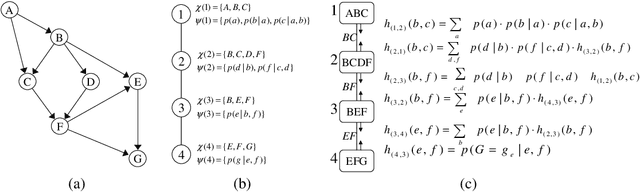
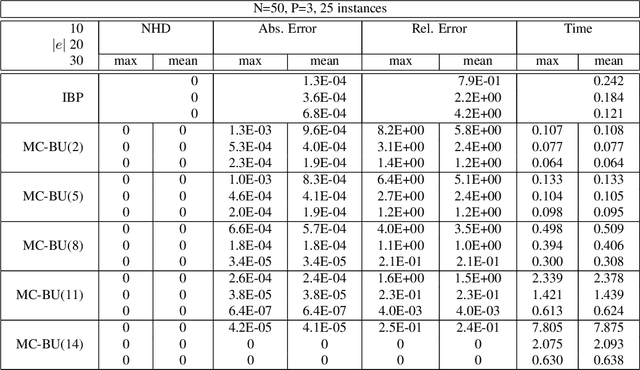
The paper investigates parameterized approximate message-passing schemes that are based on bounded inference and are inspired by Pearl's belief propagation algorithm (BP). We start with the bounded inference mini-clustering algorithm and then move to the iterative scheme called Iterative Join-Graph Propagation (IJGP), that combines both iteration and bounded inference. Algorithm IJGP belongs to the class of Generalized Belief Propagation algorithms, a framework that allowed connections with approximate algorithms from statistical physics and is shown empirically to surpass the performance of mini-clustering and belief propagation, as well as a number of other state-of-the-art algorithms on several classes of networks. We also provide insight into the accuracy of iterative BP and IJGP by relating these algorithms to well known classes of constraint propagation schemes.

AND/OR Multi-Valued Decision Diagrams for Graphical Models

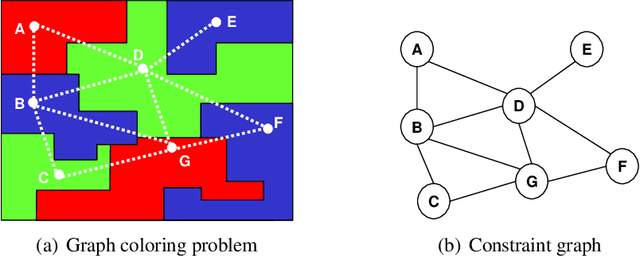
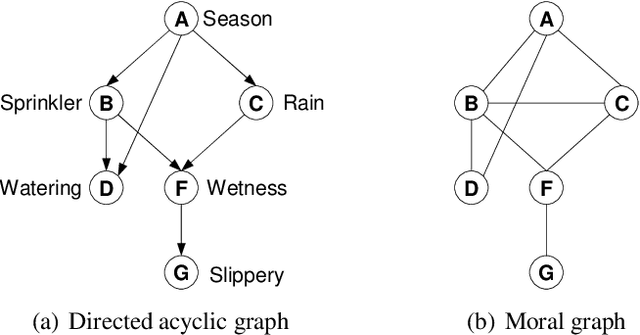
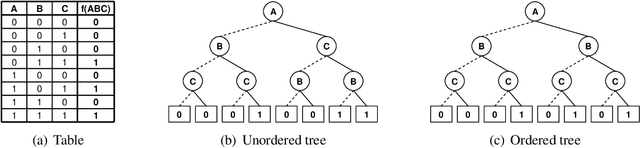
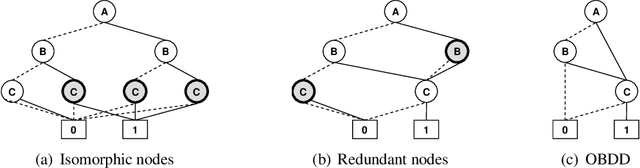
Inspired by the recently introduced framework of AND/OR search spaces for graphical models, we propose to augment Multi-Valued Decision Diagrams (MDD) with AND nodes, in order to capture function decomposition structure and to extend these compiled data structures to general weighted graphical models (e.g., probabilistic models). We present the AND/OR Multi-Valued Decision Diagram (AOMDD) which compiles a graphical model into a canonical form that supports polynomial (e.g., solution counting, belief updating) or constant time (e.g. equivalence of graphical models) queries. We provide two algorithms for compiling the AOMDD of a graphical model. The first is search-based, and works by applying reduction rules to the trace of the memory intensive AND/OR search algorithm. The second is inference-based and uses a Bucket Elimination schedule to combine the AOMDDs of the input functions via the the APPLY operator. For both algorithms, the compilation time and the size of the AOMDD are, in the worst case, exponential in the treewidth of the graphical model, rather than pathwidth as is known for ordered binary decision diagrams (OBDDs). We introduce the concept of semantic treewidth, which helps explain why the size of a decision diagram is often much smaller than the worst case bound. We provide an experimental evaluation that demonstrates the potential of AOMDDs.

Identifying Independencies in Causal Graphs with Feedback

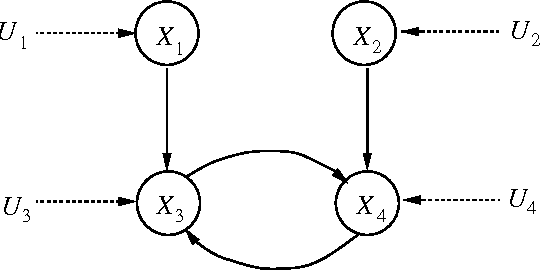
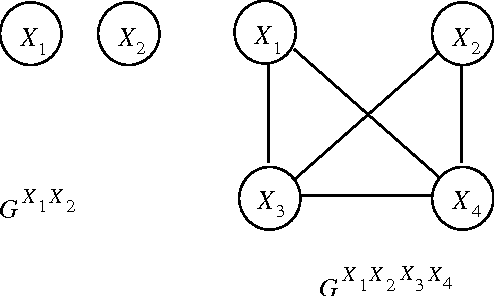
We show that the d -separation criterion constitutes a valid test for conditional independence relationships that are induced by feedback systems involving discrete variables.