Active Tuples-based Scheme for Bounding Posterior Beliefs

The paper presents a scheme for computing lower and upper bounds on the posterior marginals in Bayesian networks with discrete variables. Its power lies in its ability to use any available scheme that bounds the probability of evidence or posterior marginals and enhance its performance in an anytime manner. The scheme uses the cutset conditioning principle to tighten existing bounding schemes and to facilitate anytime behavior, utilizing a fixed number of cutset tuples. The accuracy of the bounds improves as the number of used cutset tuples increases and so does the computation time. We demonstrate empirically the value of our scheme for bounding posterior marginals and probability of evidence using a variant of the bound propagation algorithm as a plug-in scheme.

An Empirical Study of w-Cutset Sampling for Bayesian Networks

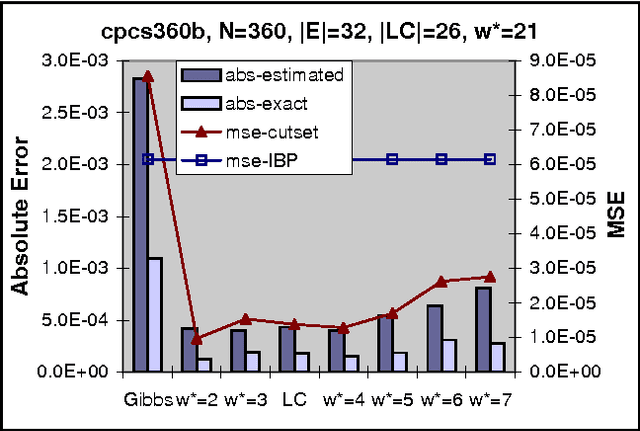
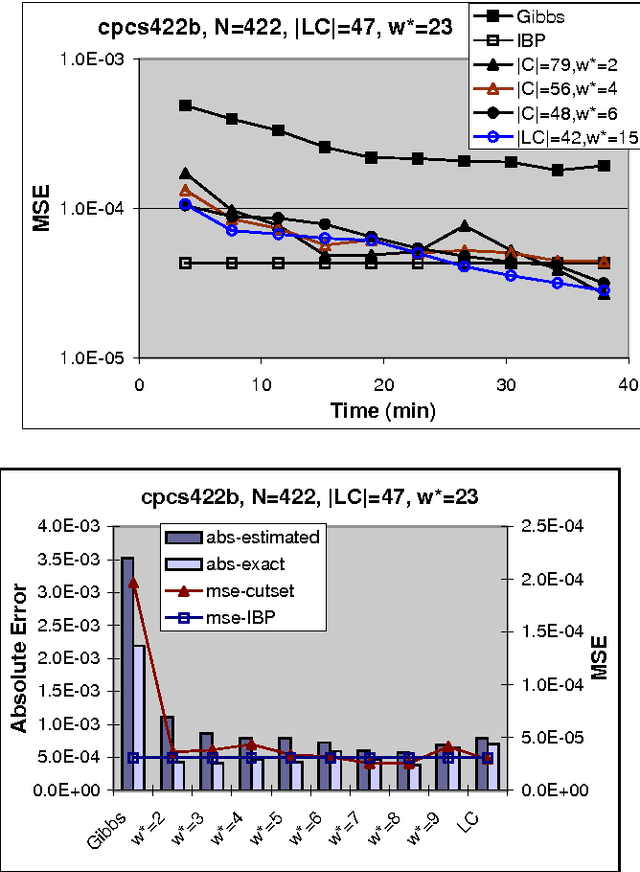
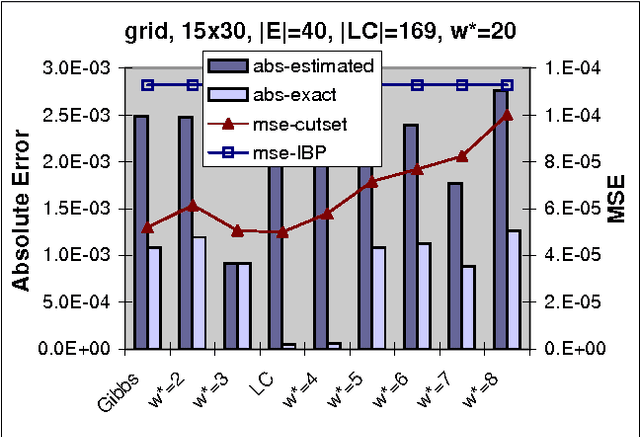
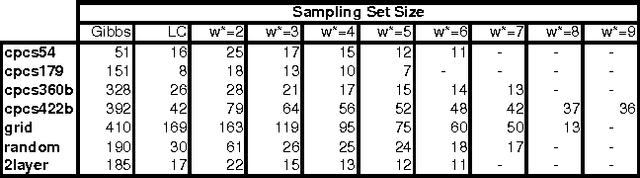
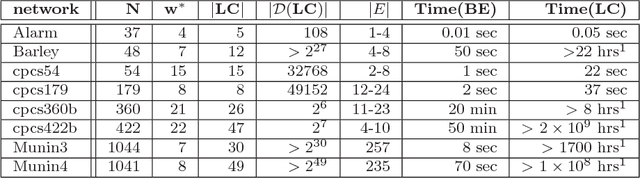
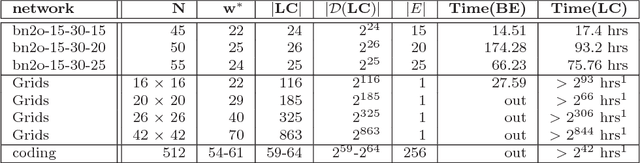
The paper studies empirically the time-space trade-off between sampling and inference in a sl cutset sampling algorithm. The algorithm samples over a subset of nodes in a Bayesian network and applies exact inference over the rest. Consequently, while the size of the sampling space decreases, requiring less samples for convergence, the time for generating each single sample increases. The w-cutset sampling selects a sampling set such that the induced-width of the network when the sampling set is observed is bounded by w, thus requiring inference whose complexity is exponential in w. In this paper, we investigate performance of w-cutset sampling over a range of w values and measure the accuracy of w-cutset sampling as a function of w. Our experiments demonstrate that the cutset sampling idea is quite powerful showing that an optimal balance between inference and sampling benefits substantially from restricting the cutset size, even at the cost of more complex inference.

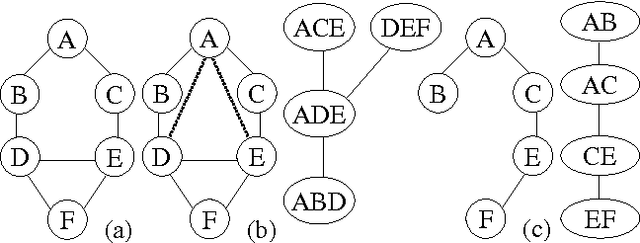
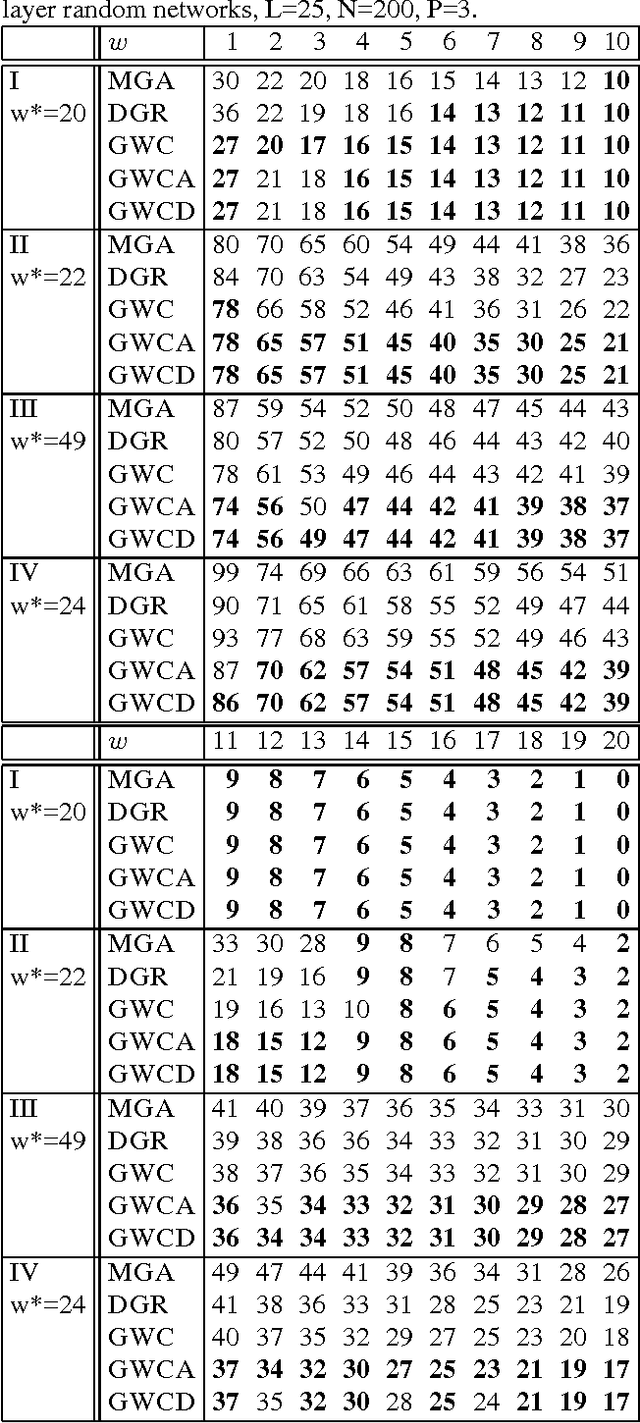
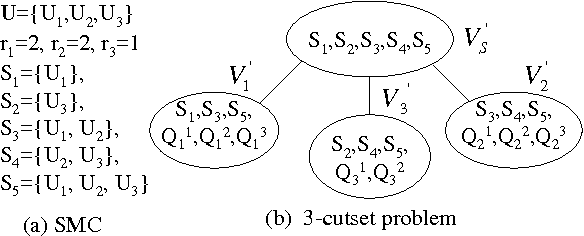
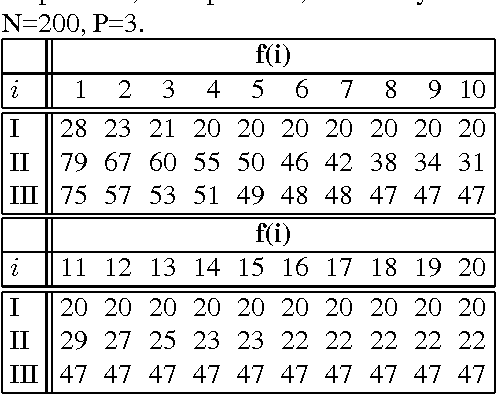
On finding minimal w-cutset

The complexity of a reasoning task over a graphical model is tied to the induced width of the underlying graph. It is well-known that the conditioning (assigning values) on a subset of variables yields a subproblem of the reduced complexity where instantiated variables are removed. If the assigned variables constitute a cycle-cutset, the rest of the network is singly-connected and therefore can be solved by linear propagation algorithms. A w-cutset is a generalization of a cycle-cutset defined as a subset of nodes such that the subgraph with cutset nodes removed has induced-width of w or less. In this paper we address the problem of finding a minimal w-cutset in a graph. We relate the problem to that of finding the minimal w-cutset of a treedecomposition. The latter can be mapped to the well-known set multi-cover problem. This relationship yields a proof of NP-completeness on one hand and a greedy algorithm for finding a w-cutset of a tree decomposition on the other. Empirical evaluation of the algorithms is presented.

Modeling Transportation Routines using Hybrid Dynamic Mixed Networks

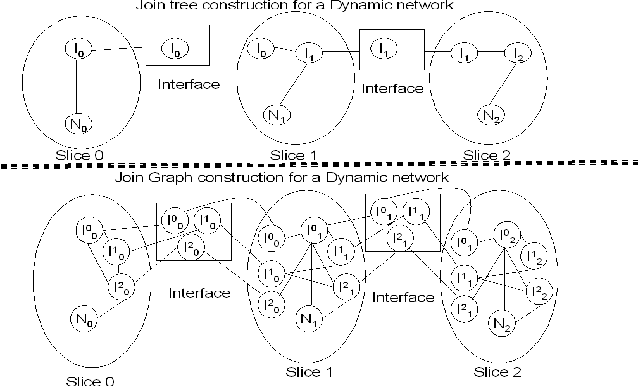
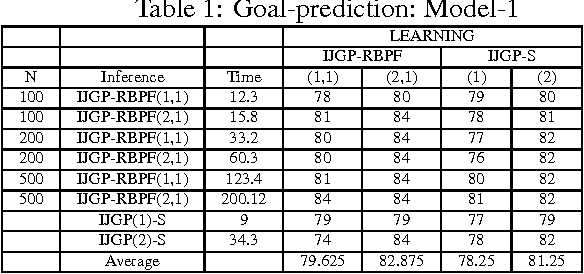
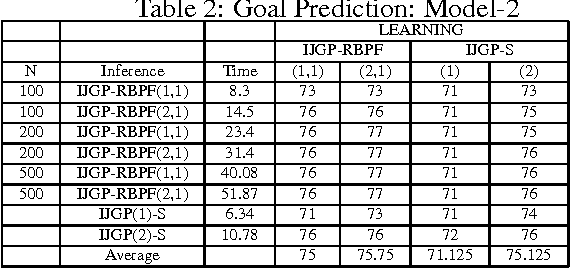
This paper describes a general framework called Hybrid Dynamic Mixed Networks (HDMNs) which are Hybrid Dynamic Bayesian Networks that allow representation of discrete deterministic information in the form of constraints. We propose approximate inference algorithms that integrate and adjust well known algorithmic principles such as Generalized Belief Propagation, Rao-Blackwellised Particle Filtering and Constraint Propagation to address the complexity of modeling and reasoning in HDMNs. We use this framework to model a person's travel activity over time and to predict destination and routes given the current location. We present a preliminary empirical evaluation demonstrating the effectiveness of our modeling framework and algorithms using several variants of the activity model.

Cutset Sampling with Likelihood Weighting

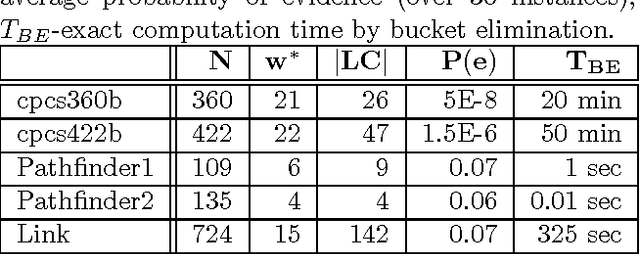
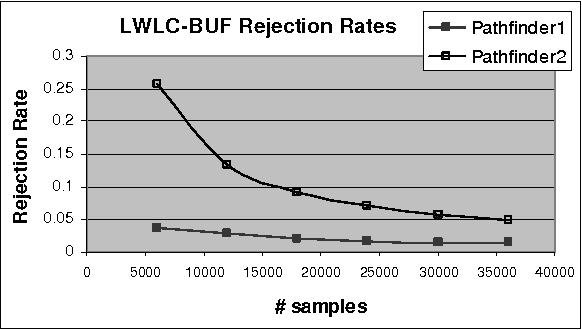
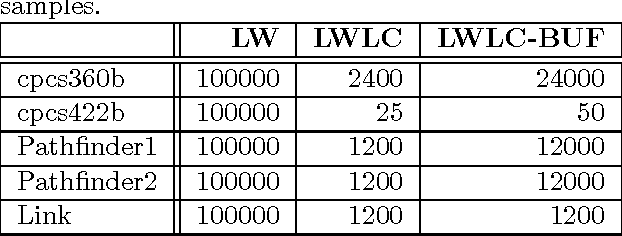
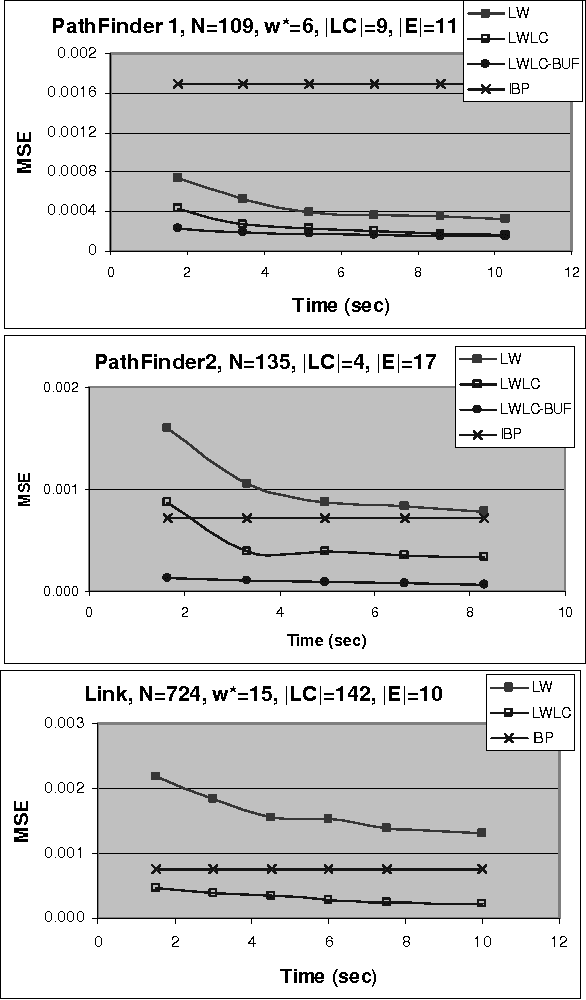
The paper analyzes theoretically and empirically the performance of likelihood weighting (LW) on a subset of nodes in Bayesian networks. The proposed scheme requires fewer samples to converge due to reduction in sampling variance. The method exploits the structure of the network to bound the complexity of exact inference used to compute sampling distributions, similar to Gibbs cutset sampling. Yet, the extension of the previosly proposed cutset sampling principles to likelihood weighting is non-trivial due to differences in the sampling processes of Gibbs sampler and LW. We demonstrate empirically that likelihood weighting on a cutset (LWLC) is effective time-wise and has a lower rejection rate than LW when applied to networks with many deterministic probabilities. Finally, we show that the performance of likelihood weighting on a cutset can be improved further by caching computed sampling distributions and, consequently, learning 'zeros' of the target distribution.

Studies in Lower Bounding Probabilities of Evidence using the Markov Inequality

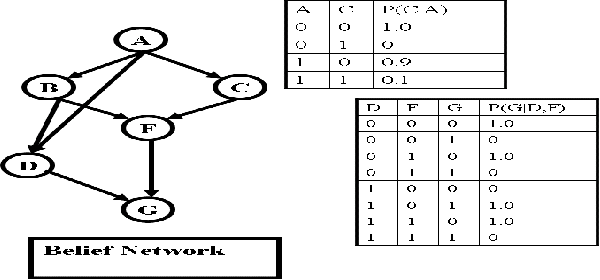
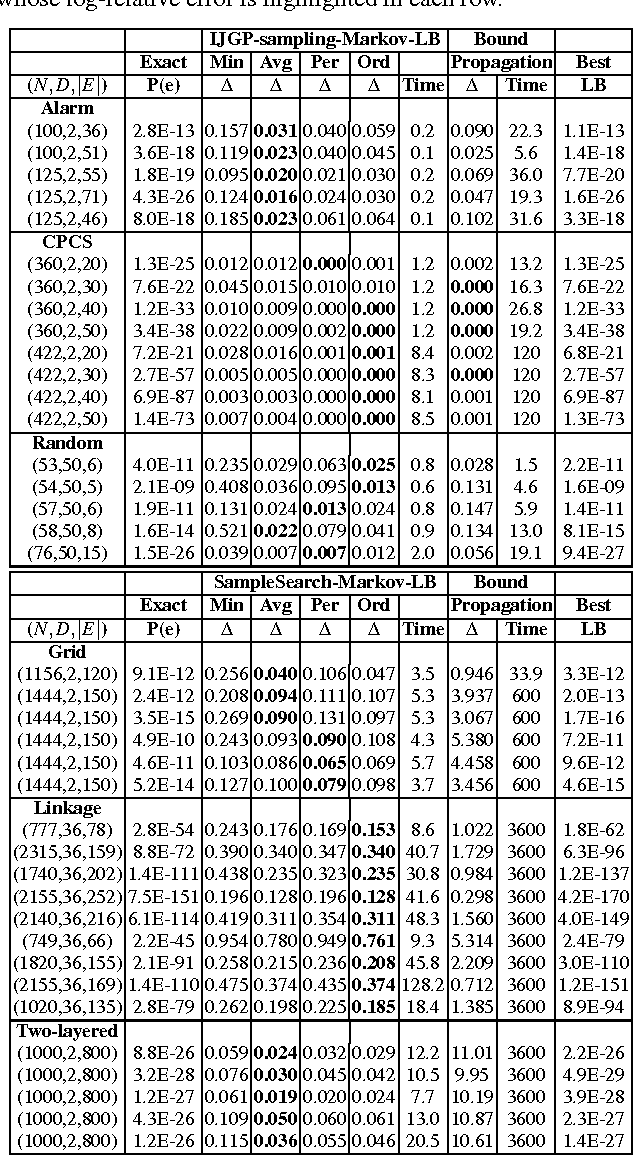
Computing the probability of evidence even with known error bounds is NP-hard. In this paper we address this hard problem by settling on an easier problem. We propose an approximation which provides high confidence lower bounds on probability of evidence but does not have any guarantees in terms of relative or absolute error. Our proposed approximation is a randomized importance sampling scheme that uses the Markov inequality. However, a straight-forward application of the Markov inequality may lead to poor lower bounds. We therefore propose several heuristic measures to improve its performance in practice. Empirical evaluation of our scheme with state-of- the-art lower bounding schemes reveals the promise of our approach.