Judea Pearl
Epsilon-Identifiability of Causal Quantities
Jan 27, 2023Abstract:Identifying the effects of causes and causes of effects is vital in virtually every scientific field. Often, however, the needed probabilities may not be fully identifiable from the data sources available. This paper shows how partial identifiability is still possible for several probabilities of causation. We term this epsilon-identifiability and demonstrate its usefulness in cases where the behavior of certain subpopulations can be restricted to within some narrow bounds. In particular, we show how unidentifiable causal effects and counterfactual probabilities can be narrowly bounded when such allowances are made. Often those allowances are easily measured and reasonably assumed. Finally, epsilon-identifiability is applied to the unit selection problem.
Probabilities of Causation: Role of Observational Data
Oct 17, 2022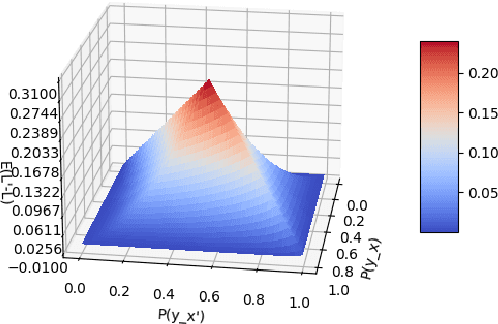
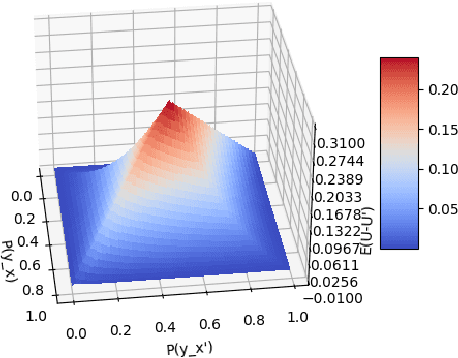

Abstract:Probabilities of causation play a crucial role in modern decision-making. Pearl defined three binary probabilities of causation, the probability of necessity and sufficiency (PNS), the probability of sufficiency (PS), and the probability of necessity (PN). These probabilities were then bounded by Tian and Pearl using a combination of experimental and observational data. However, observational data are not always available in practice; in such a case, Tian and Pearl's Theorem provided valid but less effective bounds using pure experimental data. In this paper, we discuss the conditions that observational data are worth considering to improve the quality of the bounds. More specifically, we defined the expected improvement of the bounds by assuming the observational distributions are uniformly distributed on their feasible interval. We further applied the proposed theorems to the unit selection problem defined by Li and Pearl.
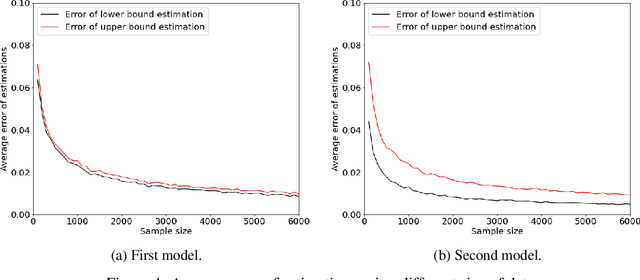
Learning Probabilities of Causation from Finite Population Data
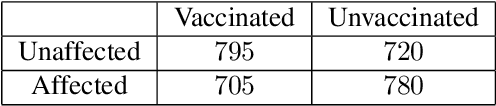
Oct 16, 2022
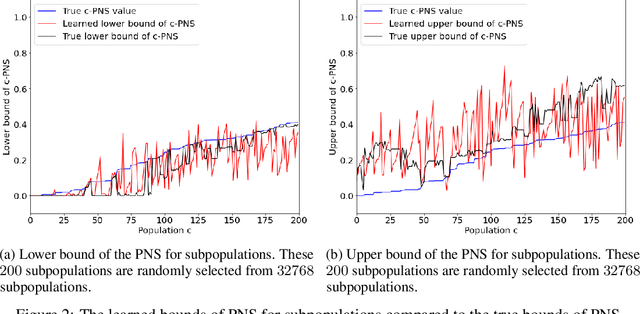
Abstract:This paper deals with the problem of learning the probabilities of causation of subpopulations given finite population data. The tight bounds of three basic probabilities of causation, the probability of necessity and sufficiency (PNS), the probability of sufficiency (PS), and the probability of necessity (PN), were derived by Tian and Pearl. However, obtaining the bounds for each subpopulation requires experimental and observational distributions of each subpopulation, which is usually impractical to estimate given finite population data. We propose a machine learning model that helps to learn the bounds of the probabilities of causation for subpopulations given finite population data. We further show by a simulated study that the machine learning model is able to learn the bounds of PNS for 32768 subpopulations with only knowing roughly 500 of them from the finite population data.
Unit Selection: Learning Benefit Function from Finite Population Data
Oct 15, 2022
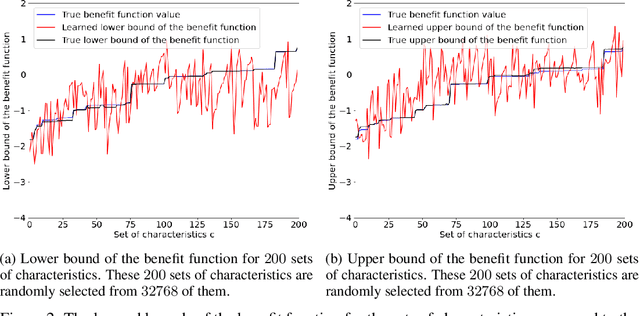
Abstract:The unit selection problem is to identify a group of individuals who are most likely to exhibit a desired mode of behavior, for example, selecting individuals who would respond one way if incentivized and a different way if not. The unit selection problem consists of evaluation and search subproblems. Li and Pearl defined the "benefit function" to evaluate the average payoff of selecting a certain individual with given characteristics. The search subproblem is then to design an algorithm to identify the characteristics that maximize the above benefit function. The hardness of the search subproblem arises due to the large number of characteristics available for each individual and the sparsity of the data available in each cell of characteristics. In this paper, we present a machine learning framework that uses the bounds of the benefit function that are estimable from the finite population data to learn the bounds of the benefit function for each cell of characteristics. Therefore, we could easily obtain the characteristics that maximize the benefit function.
Unit Selection: Case Study and Comparison with A/B Test Heuristic
Oct 10, 2022
Abstract:The unit selection problem defined by Li and Pearl identifies individuals who have desired counterfactual behavior patterns, for example, individuals who would respond positively if encouraged and would not otherwise. Li and Pearl showed by example that their unit selection model is beyond the A/B test heuristics. In this paper, we reveal the essence of the A/B test heuristics, which are exceptional cases of the benefit function defined by Li and Pearl. Furthermore, We provided more simulated use cases of Li-Pearl's unit selection model to help decision-makers apply their model correctly, explaining that A/B test heuristics are generally problematic.
Probabilities of Causation: Adequate Size of Experimental and Observational Samples
Oct 10, 2022
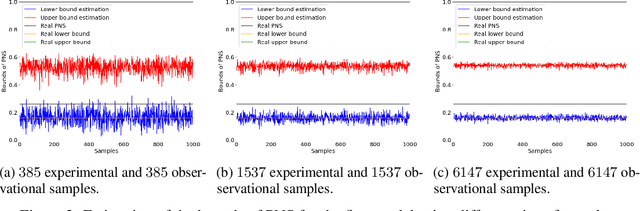
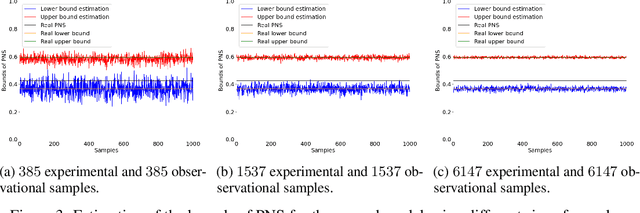
Abstract:The probabilities of causation are commonly used to solve decision-making problems. Tian and Pearl derived sharp bounds for the probability of necessity and sufficiency (PNS), the probability of sufficiency (PS), and the probability of necessity (PN) using experimental and observational data. The assumption is that one is in possession of a large enough sample to permit an accurate estimation of the experimental and observational distributions. In this study, we present a method for determining the sample size needed for such estimation, when a given confidence interval (CI) is specified. We further show by simulation that the proposed sample size delivered stable estimations of the bounds of PNS.
Unit Selection with Nonbinary Treatment and Effect
Aug 20, 2022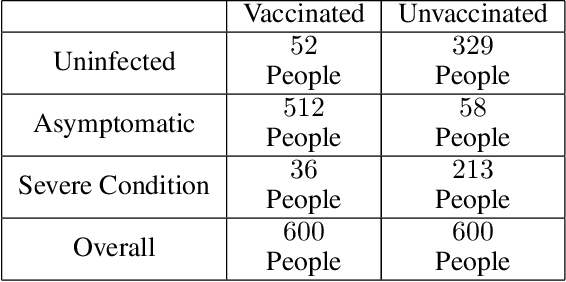
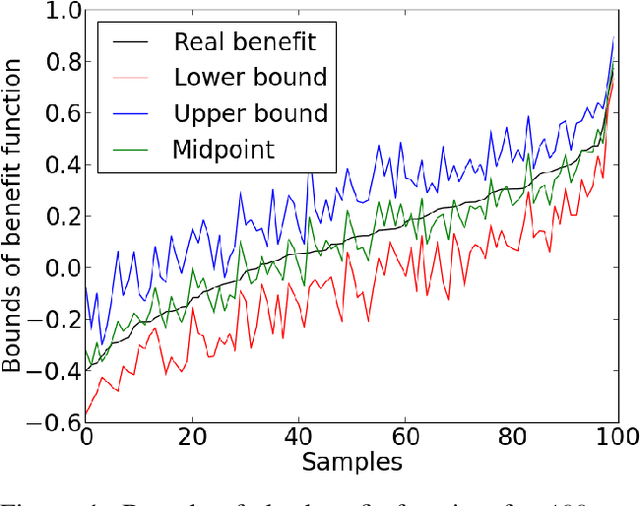
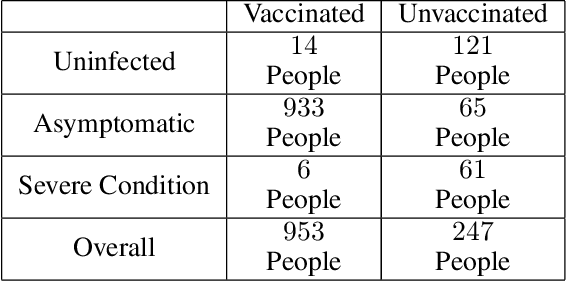
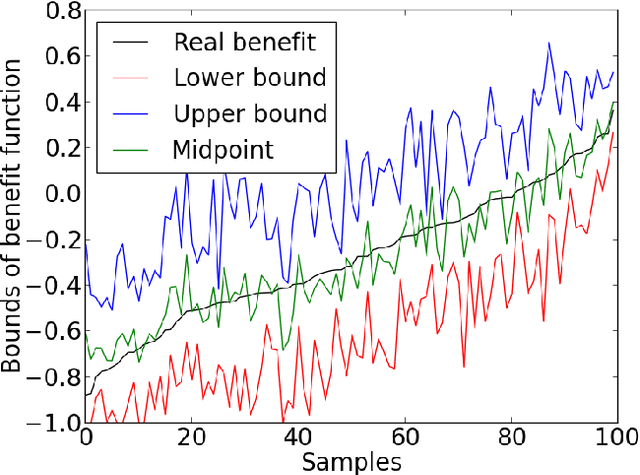
Abstract:The unit selection problem aims to identify a set of individuals who are most likely to exhibit a desired mode of behavior, for example, selecting individuals who would respond one way if encouraged and a different way if not encouraged. Using a combination of experimental and observational data, Li and Pearl derived tight bounds on the "benefit function", which is the payoff/cost associated with selecting an individual with given characteristics. This paper extends the benefit function to the general form such that the treatment and effect are not restricted to binary. We propose an algorithm to test the identifiability of the nonbinary benefit function and an algorithm to compute the bounds of the nonbinary benefit function using experimental and observational data.
Probabilities of Causation with Nonbinary Treatment and Effect
Aug 19, 2022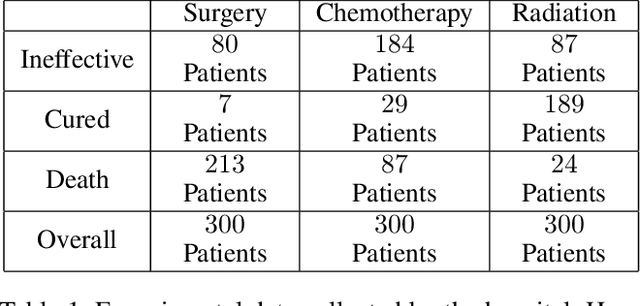
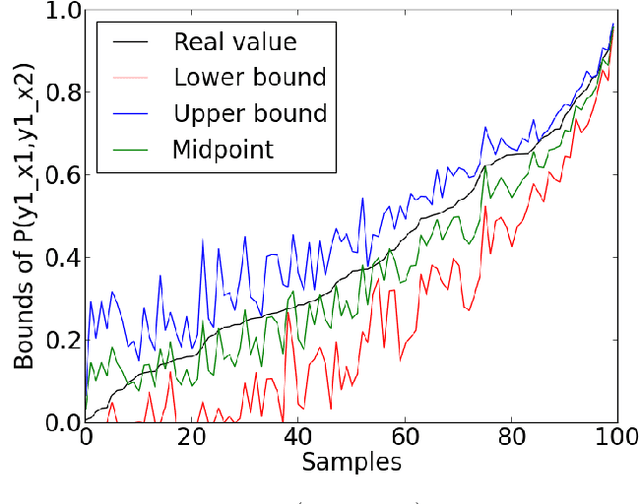
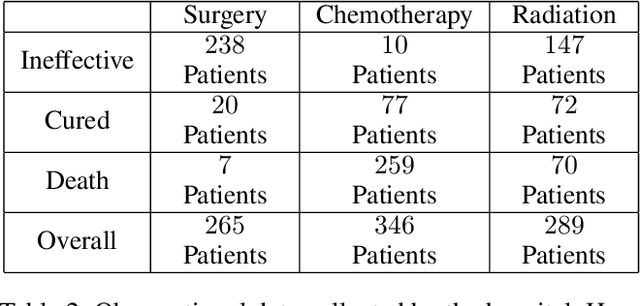
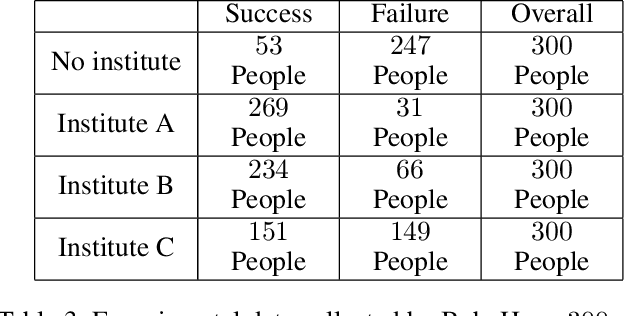
Abstract:This paper deals with the problem of estimating the probabilities of causation when treatment and effect are not binary. Tian and Pearl derived sharp bounds for the probability of necessity and sufficiency (PNS), the probability of sufficiency (PS), and the probability of necessity (PN) using experimental and observational data. In this paper, we provide theoretical bounds for all types of probabilities of causation to multivalued treatments and effects. We further discuss examples where our bounds guide practical decisions and use simulation studies to evaluate how informative the bounds are for various combinations of data.
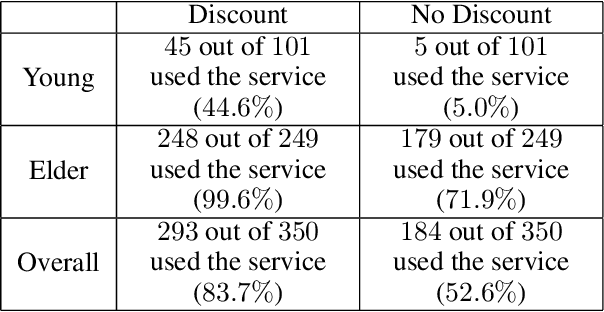
Personalized Decision Making -- A Conceptual Introduction
Aug 19, 2022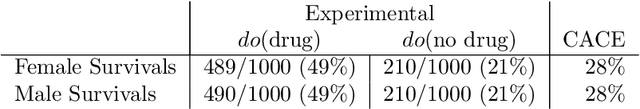
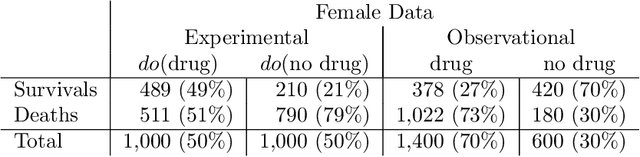
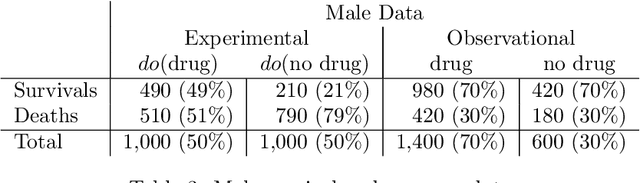
Abstract:Personalized decision making targets the behavior of a specific individual, while population-based decision making concerns a sub-population resembling that individual. This paper clarifies the distinction between the two and explains why the former leads to more informed decisions. We further show that by combining experimental and observational studies we can obtain valuable information about individual behavior and, consequently, improve decisions over those obtained from experimental studies alone.
Unit Selection with Causal Diagram
Sep 15, 2021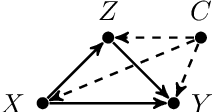
Abstract:The unit selection problem aims to identify a set of individuals who are most likely to exhibit a desired mode of behavior, for example, selecting individuals who would respond one way if encouraged and a different way if not encouraged. Using a combination of experimental and observational data, Li and Pearl derived tight bounds on the "benefit function" - the payoff/cost associated with selecting an individual with given characteristics. This paper shows that these bounds can be narrowed significantly (enough to change decisions) when structural information is available in the form of a causal model. We address the problem of estimating the benefit function using observational and experimental data when specific graphical criteria are assumed to hold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge