Join-Graph Propagation Algorithms

The paper investigates parameterized approximate message-passing schemes that are based on bounded inference and are inspired by Pearl's belief propagation algorithm (BP). We start with the bounded inference mini-clustering algorithm and then move to the iterative scheme called Iterative Join-Graph Propagation (IJGP), that combines both iteration and bounded inference. Algorithm IJGP belongs to the class of Generalized Belief Propagation algorithms, a framework that allowed connections with approximate algorithms from statistical physics and is shown empirically to surpass the performance of mini-clustering and belief propagation, as well as a number of other state-of-the-art algorithms on several classes of networks. We also provide insight into the accuracy of iterative BP and IJGP by relating these algorithms to well known classes of constraint propagation schemes.

AND/OR Multi-Valued Decision Diagrams for Graphical Models

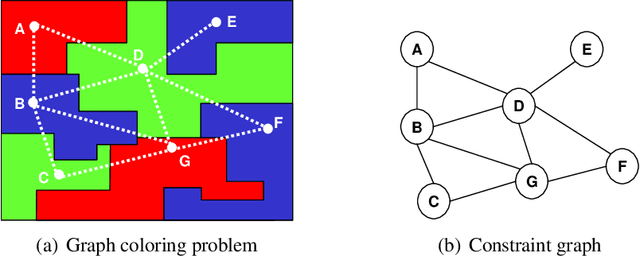
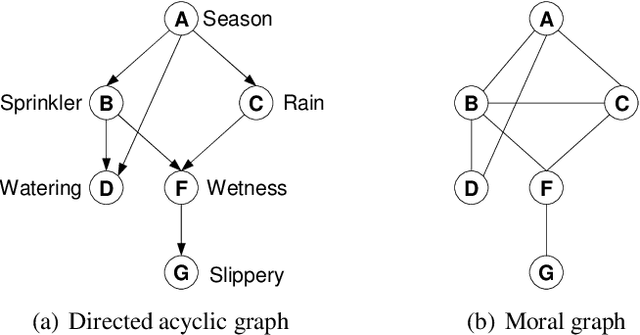
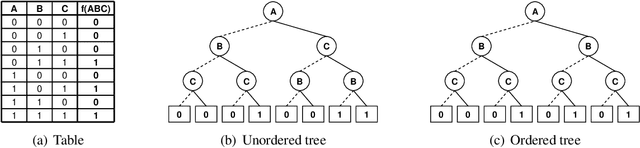
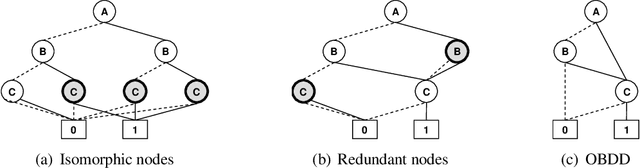
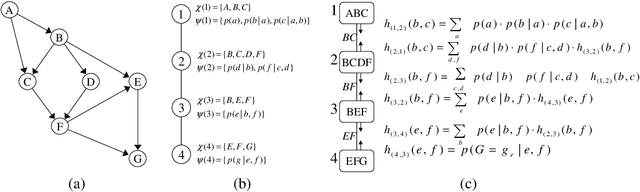
Inspired by the recently introduced framework of AND/OR search spaces for graphical models, we propose to augment Multi-Valued Decision Diagrams (MDD) with AND nodes, in order to capture function decomposition structure and to extend these compiled data structures to general weighted graphical models (e.g., probabilistic models). We present the AND/OR Multi-Valued Decision Diagram (AOMDD) which compiles a graphical model into a canonical form that supports polynomial (e.g., solution counting, belief updating) or constant time (e.g. equivalence of graphical models) queries. We provide two algorithms for compiling the AOMDD of a graphical model. The first is search-based, and works by applying reduction rules to the trace of the memory intensive AND/OR search algorithm. The second is inference-based and uses a Bucket Elimination schedule to combine the AOMDDs of the input functions via the the APPLY operator. For both algorithms, the compilation time and the size of the AOMDD are, in the worst case, exponential in the treewidth of the graphical model, rather than pathwidth as is known for ordered binary decision diagrams (OBDDs). We introduce the concept of semantic treewidth, which helps explain why the size of a decision diagram is often much smaller than the worst case bound. We provide an experimental evaluation that demonstrates the potential of AOMDDs.

Iterative Join-Graph Propagation

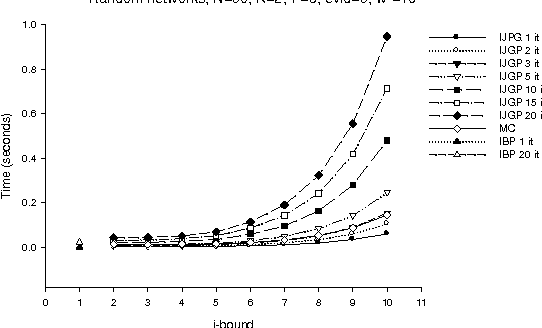
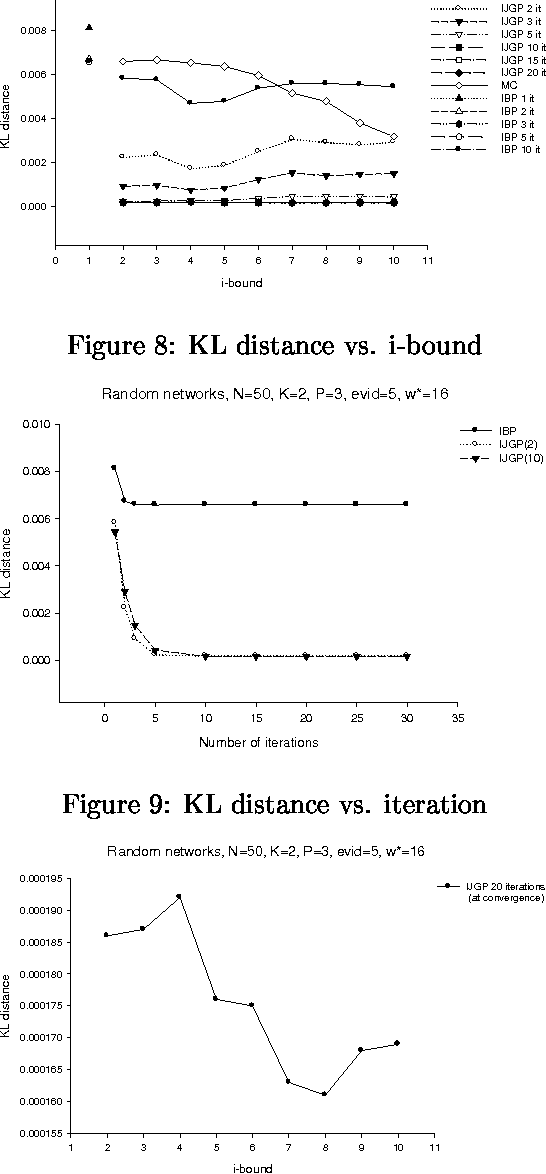
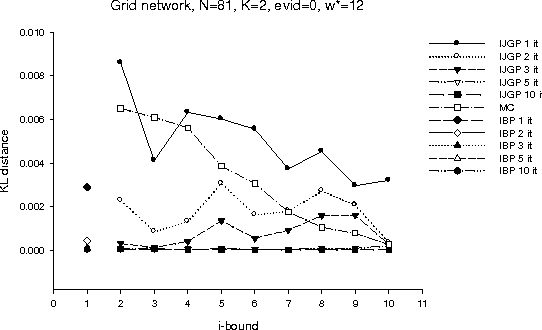
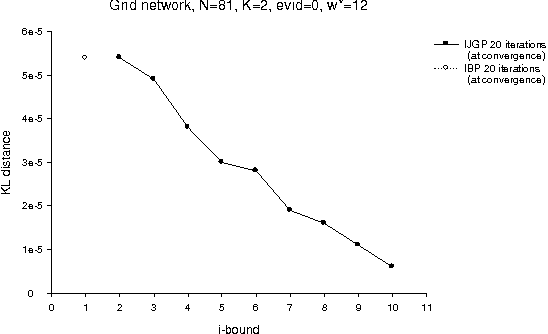
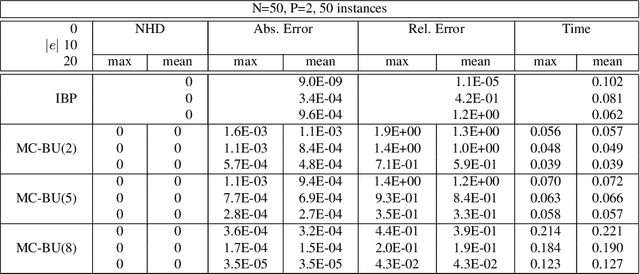
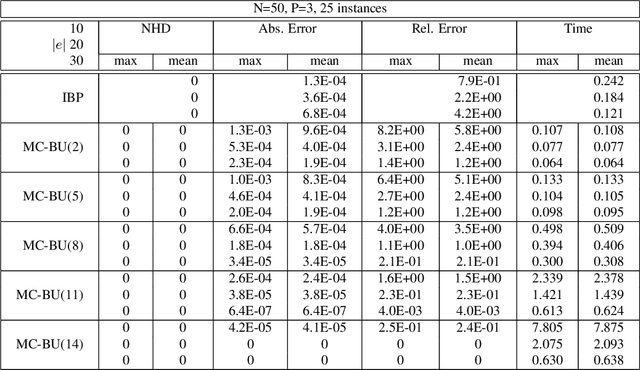
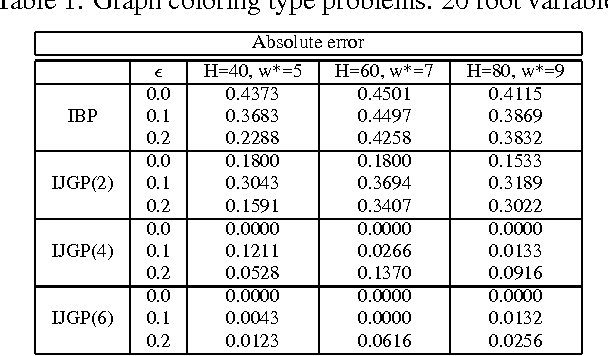
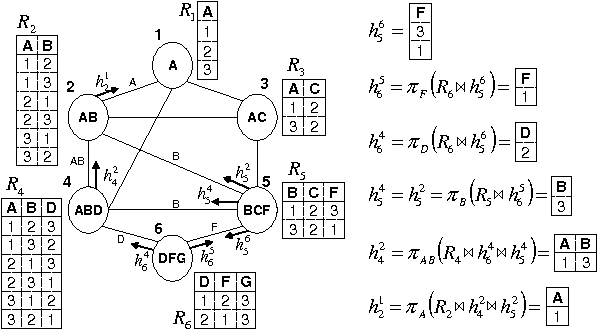
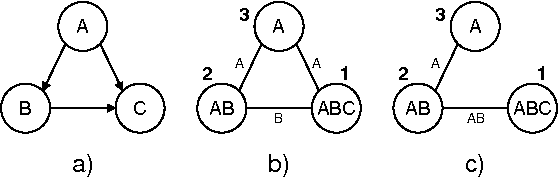
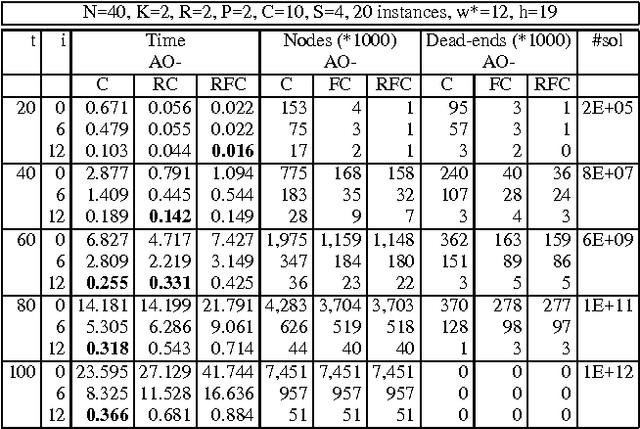
The paper presents an iterative version of join-tree clustering that applies the message passing of join-tree clustering algorithm to join-graphs rather than to join-trees, iteratively. It is inspired by the success of Pearl's belief propagation algorithm as an iterative approximation scheme on one hand, and by a recently introduced mini-clustering i. success as an anytime approximation method, on the other. The proposed Iterative Join-graph Propagation IJGP belongs to the class of generalized belief propagation methods, recently proposed using analogy with algorithms in statistical physics. Empirical evaluation of this approach on a number of problem classes demonstrates that even the most time-efficient variant is almost always superior to IBP and MC i, and is sometimes more accurate by as much as several orders of magnitude.

A Simple Insight into Iterative Belief Propagation's Success

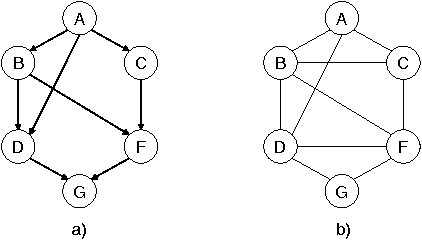
In Non - ergodic belief networks the posterior belief OF many queries given evidence may become zero.The paper shows that WHEN belief propagation IS applied iteratively OVER arbitrary networks(the so called, iterative OR loopy belief propagation(IBP)) it IS identical TO an arc - consistency algorithm relative TO zero - belief queries(namely assessing zero posterior probabilities). This implies that zero - belief conclusions derived BY belief propagation converge AND are sound.More importantly it suggests that the inference power OF IBP IS AS strong AND AS weak, AS that OF arc - consistency.This allows the synthesis OF belief networks FOR which belief propagation IS useless ON one hand, AND focuses the investigation OF classes OF belief network FOR which belief propagation may be zero - complete.Finally, ALL the above conclusions apply also TO Generalized belief propagation algorithms that extend loopy belief propagation AND allow a crisper understanding OF their power.

Mixtures of Deterministic-Probabilistic Networks and their AND/OR Search Space

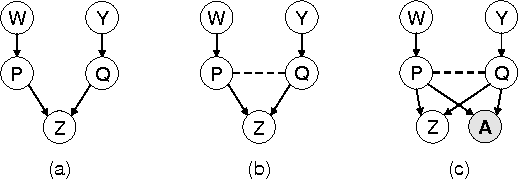
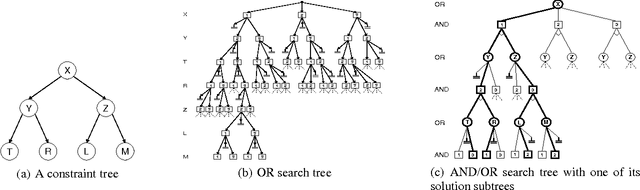
The paper introduces mixed networks, a new framework for expressing and reasoning with probabilistic and deterministic information. The framework combines belief networks with constraint networks, defining the semantics and graphical representation. We also introduce the AND/OR search space for graphical models, and develop a new linear space search algorithm. This provides the basis for understanding the benefits of processing the constraint information separately, resulting in the pruning of the search space. When the constraint part is tractable or has a small number of solutions, using the mixed representation can be exponentially more effective than using pure belief networks which odel constraints as conditional probability tables.

The Relationship Between AND/OR Search and Variable Elimination

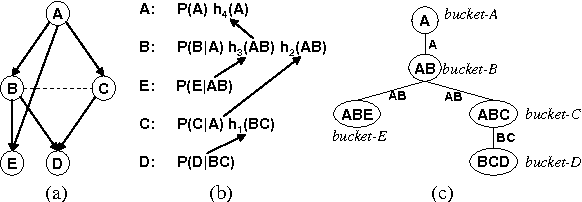
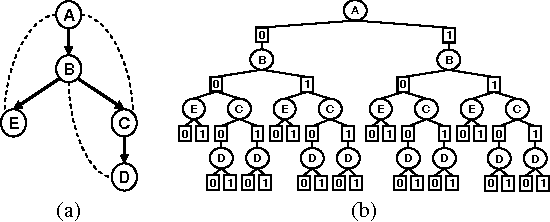
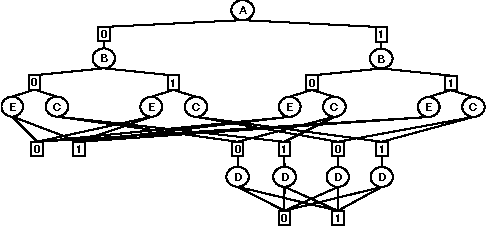
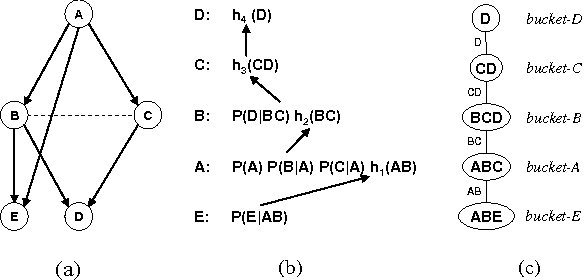
In this paper we compare search and inference in graphical models through the new framework of AND/OR search. Specifically, we compare Variable Elimination (VE) and memoryintensive AND/OR Search (AO) and place algorithms such as graph-based backjumping and no-good and good learning, as well as Recursive Conditioning [7] and Value Elimination [2] within the AND/OR search framework.

AND/OR Multi-Valued Decision Diagrams for Weighted Graphical Models

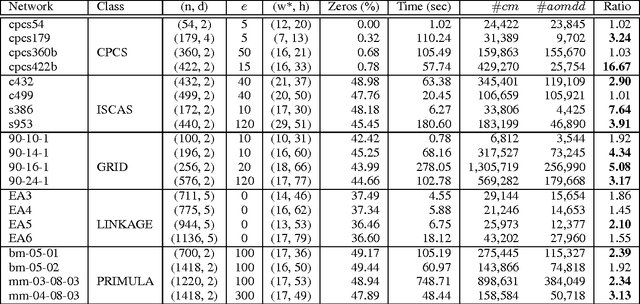
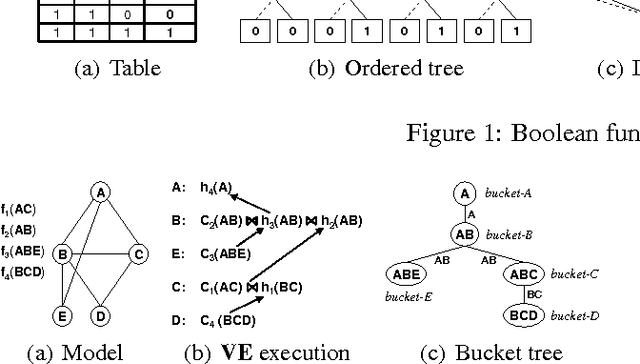
Compiling graphical models has recently been under intense investigation, especially for probabilistic modeling and processing. We present here a novel data structure for compiling weighted graphical models (in particular, probabilistic models), called AND/OR Multi-Valued Decision Diagram (AOMDD). This is a generalization of our previous work on constraint networks, to weighted models. The AOMDD is based on the frameworks of AND/OR search spaces for graphical models, and Ordered Binary Decision Diagrams (OBDD). The AOMDD is a canonical representation of a graphical model, and its size and compilation time are bounded exponentially by the treewidth of the graph, rather than pathwidth as is known for OBDDs. We discuss a Variable Elimination schedule for compilation, and present the general APPLY algorithm that combines two weighted AOMDDs, and also present a search based method for compilation method. The preliminary experimental evaluation is quite encouraging, showing the potential of the AOMDD data structure.