Pruning Attention Heads of Transformer Models Using A* Search: A Novel Approach to Compress Big NLP Architectures

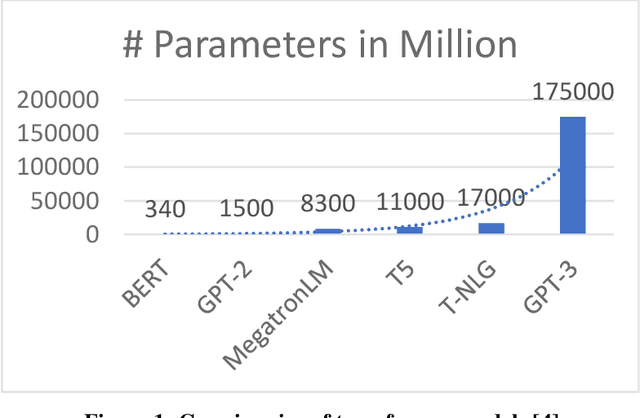
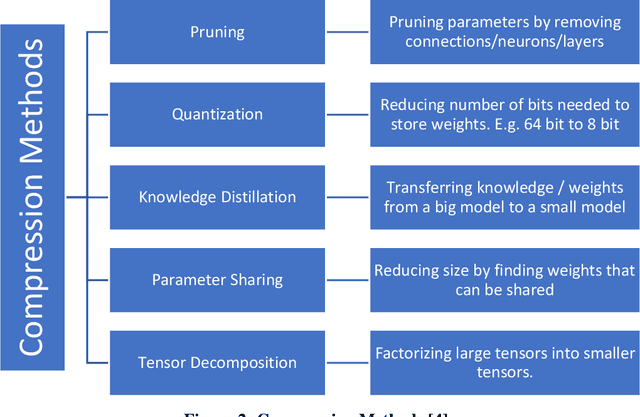
Recent years have seen a growing adoption of Transformer models such as BERT in Natural Language Processing and even in Computer Vision. However, due to their size, there has been limited adoption of such models within resource-constrained computing environments. This paper proposes novel pruning algorithm to compress transformer models by eliminating redundant Attention Heads. We apply the A* search algorithm to obtain a pruned model with strict accuracy guarantees. Our results indicate that the method could eliminate as much as 40% of the attention heads in the BERT transformer model with no loss in accuracy.

Generalized Kernel Ridge Regression for Causal Inference with Missing-at-Random Sample Selection

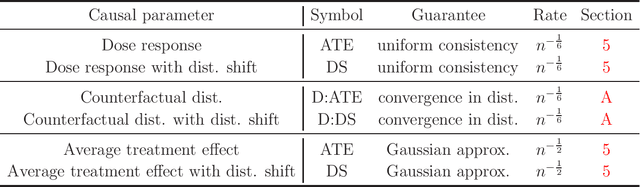
I propose kernel ridge regression estimators for nonparametric dose response curves and semiparametric treatment effects in the setting where an analyst has access to a selected sample rather than a random sample; only for select observations, the outcome is observed. I assume selection is as good as random conditional on treatment and a sufficiently rich set of observed covariates, where the covariates are allowed to cause treatment or be caused by treatment -- an extension of missingness-at-random (MAR). I propose estimators of means, increments, and distributions of counterfactual outcomes with closed form solutions in terms of kernel matrix operations, allowing treatment and covariates to be discrete or continuous, and low, high, or infinite dimensional. For the continuous treatment case, I prove uniform consistency with finite sample rates. For the discrete treatment case, I prove root-n consistency, Gaussian approximation, and semiparametric efficiency.

Kernel Methods for Multistage Causal Inference: Mediation Analysis and Dynamic Treatment Effects

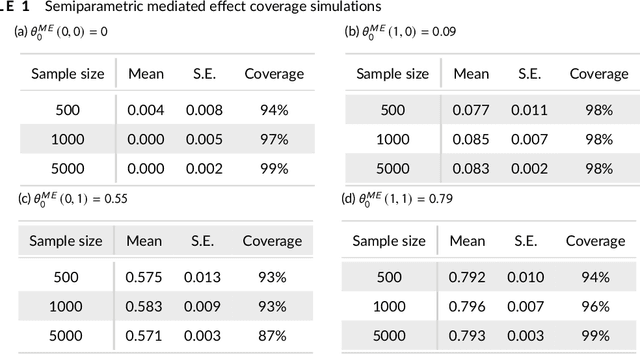
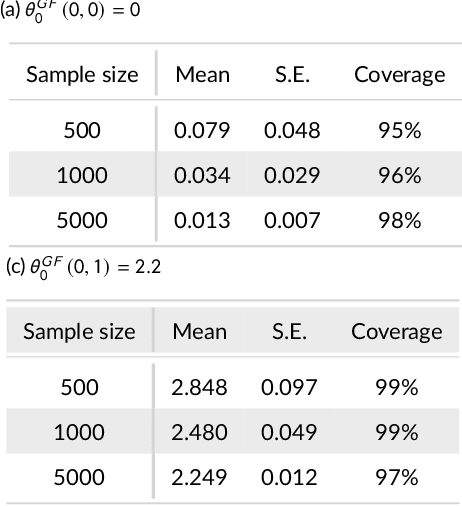
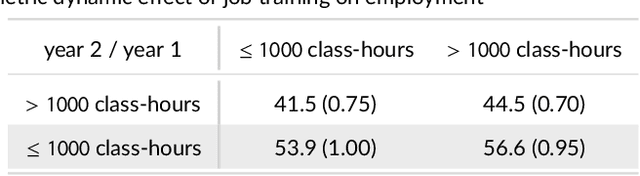
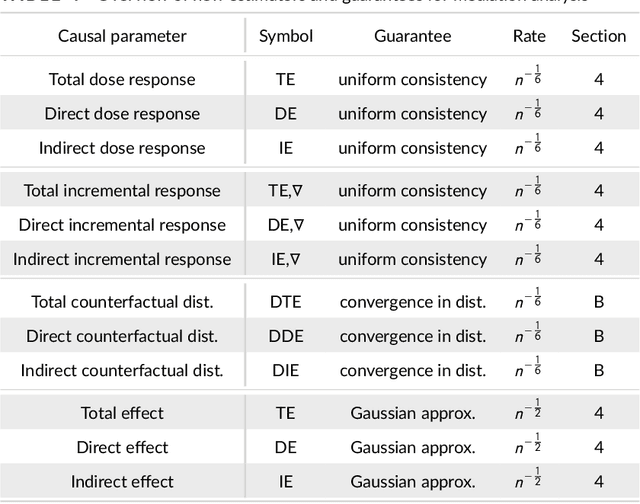
We propose kernel ridge regression estimators for mediation analysis and dynamic treatment effects over short horizons. We allow treatments, covariates, and mediators to be discrete or continuous, and low, high, or infinite dimensional. We propose estimators of means, increments, and distributions of counterfactual outcomes with closed form solutions in terms of kernel matrix operations. For the continuous treatment case, we prove uniform consistency with finite sample rates. For the discrete treatment case, we prove root-n consistency, Gaussian approximation, and semiparametric efficiency. We conduct simulations then estimate mediated and dynamic treatment effects of the US Job Corps program for disadvantaged youth.

Reinforcement Learning for Finite-Horizon Restless Multi-Armed Multi-Action Bandits

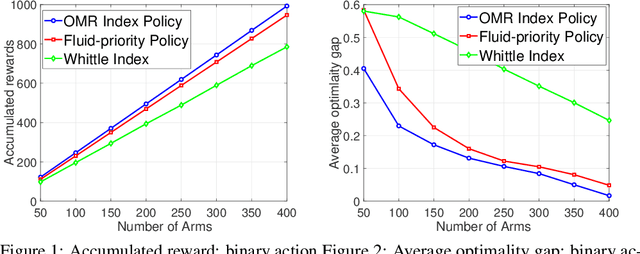
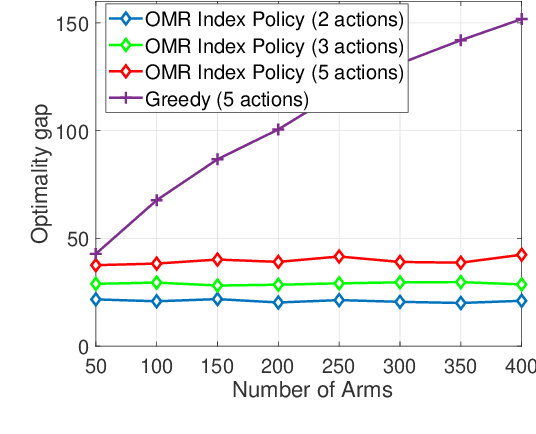
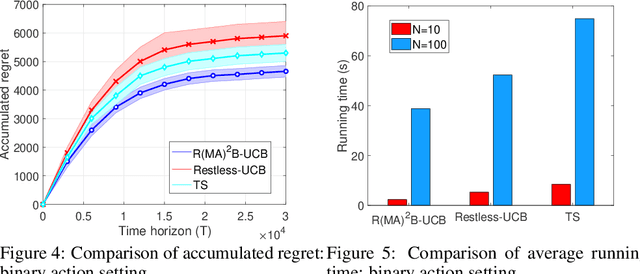
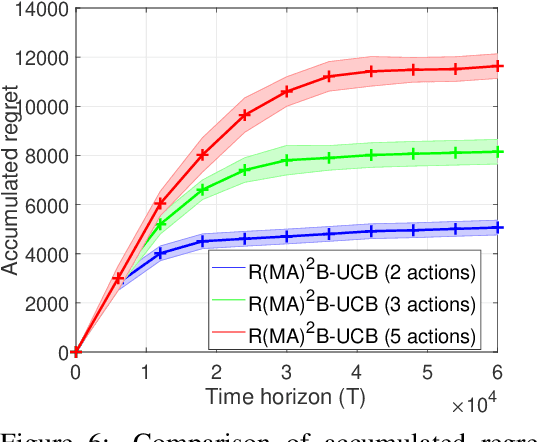
We study a finite-horizon restless multi-armed bandit problem with multiple actions, dubbed R(MA)^2B. The state of each arm evolves according to a controlled Markov decision process (MDP), and the reward of pulling an arm depends on both the current state of the corresponding MDP and the action taken. The goal is to sequentially choose actions for arms so as to maximize the expected value of the cumulative rewards collected. Since finding the optimal policy is typically intractable, we propose a computationally appealing index policy which we call Occupancy-Measured-Reward Index Policy. Our policy is well-defined even if the underlying MDPs are not indexable. We prove that it is asymptotically optimal when the activation budget and number of arms are scaled up, while keeping their ratio as a constant. For the case when the system parameters are unknown, we develop a learning algorithm. Our learning algorithm uses the principle of optimism in the face of uncertainty and further uses a generative model in order to fully exploit the structure of Occupancy-Measured-Reward Index Policy. We call it the R(MA)^2B-UCB algorithm. As compared with the existing algorithms, R(MA)^2B-UCB performs close to an offline optimum policy, and also achieves a sub-linear regret with a low computational complexity. Experimental results show that R(MA)^2B-UCB outperforms the existing algorithms in both regret and run time.

Inference of collective Gaussian hidden Markov models

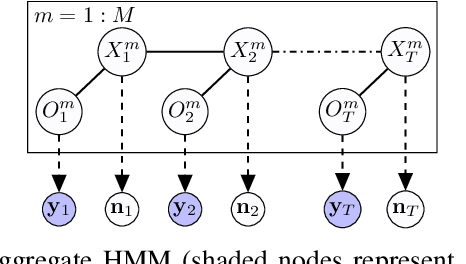
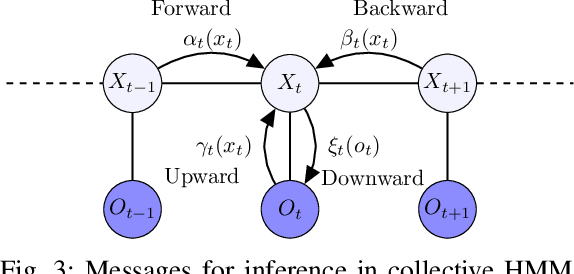
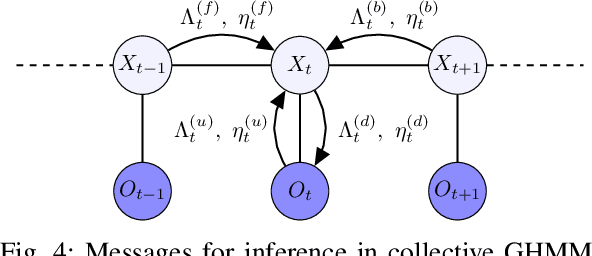
We consider inference problems for a class of continuous state collective hidden Markov models, where the data is recorded in aggregate (collective) form generated by a large population of individuals following the same dynamics. We propose an aggregate inference algorithm called collective Gaussian forward-backward algorithm, extending recently proposed Sinkhorn belief propagation algorithm to models characterized by Gaussian densities. Our algorithm enjoys convergence guarantee. In addition, it reduces to the standard Kalman filter when the observations are generated by a single individual. The efficacy of the proposed algorithm is demonstrated through multiple experiments.

Causal Inference with Corrupted Data: Measurement Error, Missing Values, Discretization, and Differential Privacy

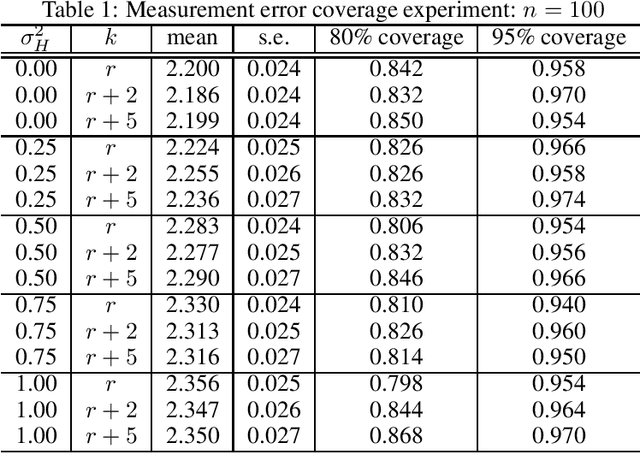
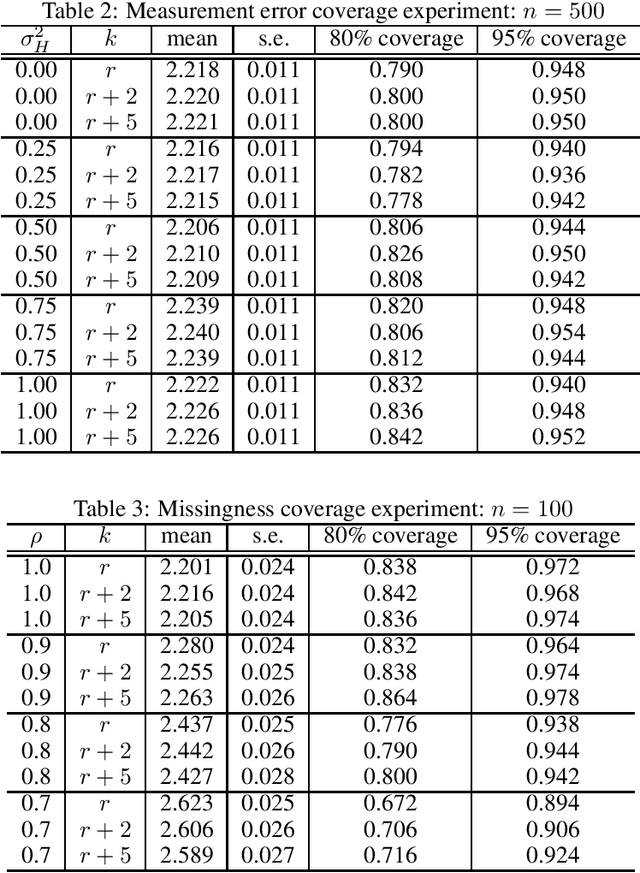
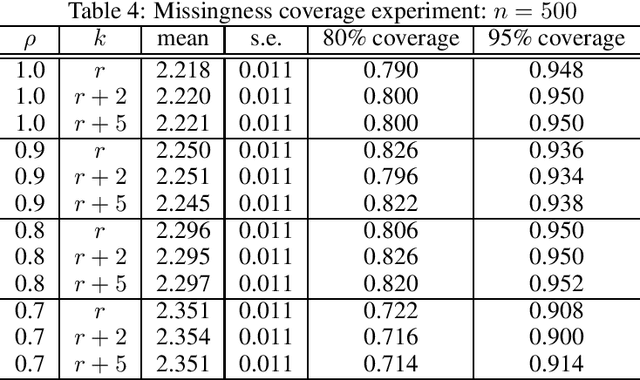
Even the most carefully curated economic data sets have variables that are noisy, missing, discretized, or privatized. The standard workflow for empirical research involves data cleaning followed by data analysis that typically ignores the bias and variance consequences of data cleaning. We formulate a semiparametric model for causal inference with corrupted data to encompass both data cleaning and data analysis. We propose a new end-to-end procedure for data cleaning, estimation, and inference with data cleaning-adjusted confidence intervals. We prove root-n consistency, Gaussian approximation, and semiparametric efficiency for our estimator of the causal parameter by finite sample arguments. Our key assumption is that the true covariates are approximately low rank. In our analysis, we provide nonasymptotic theoretical contributions to matrix completion, statistical learning, and semiparametric statistics. We verify the coverage of the data cleaning-adjusted confidence intervals in simulations.

A Simple and General Debiased Machine Learning Theorem with Finite Sample Guarantees

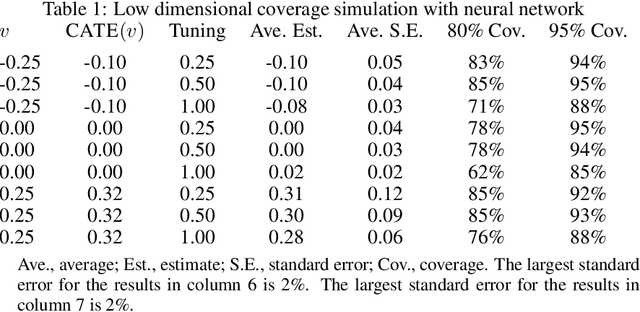
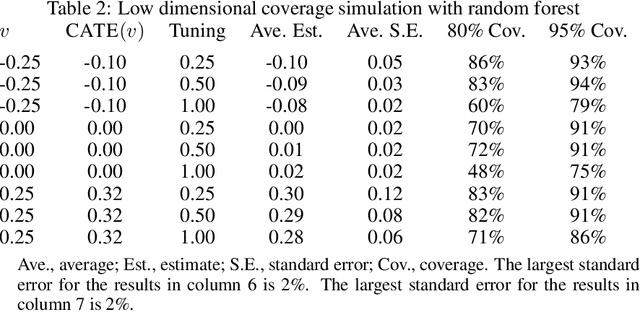
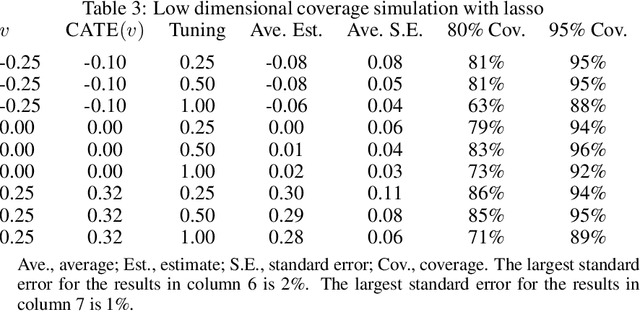
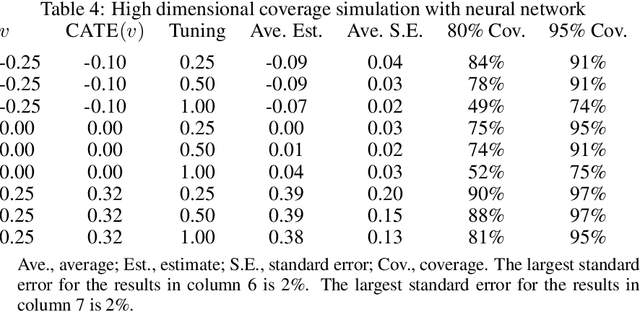
Debiased machine learning is a meta algorithm based on bias correction and sample splitting to calculate confidence intervals for functionals (i.e. scalar summaries) of machine learning algorithms. For example, an analyst may desire the confidence interval for a treatment effect estimated with a neural network. We provide a nonasymptotic debiased machine learning theorem that encompasses any global or local functional of any machine learning algorithm that satisfies a few simple, interpretable conditions. Formally, we prove consistency, Gaussian approximation, and semiparametric efficiency by finite sample arguments. The rate of convergence is root-n for global functionals, and it degrades gracefully for local functionals. Our results culminate in a simple set of conditions that an analyst can use to translate modern learning theory rates into traditional statistical inference. The conditions reveal a new double robustness property for ill posed inverse problems.

Self-interpretable Convolutional Neural Networks for Text Classification

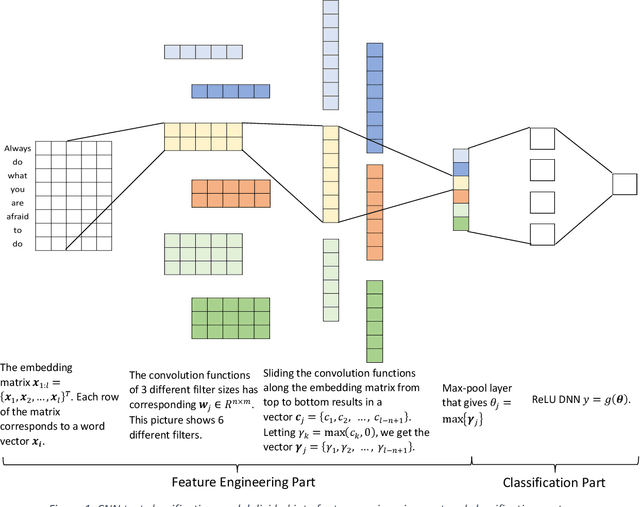
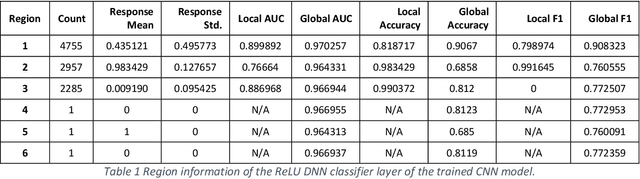
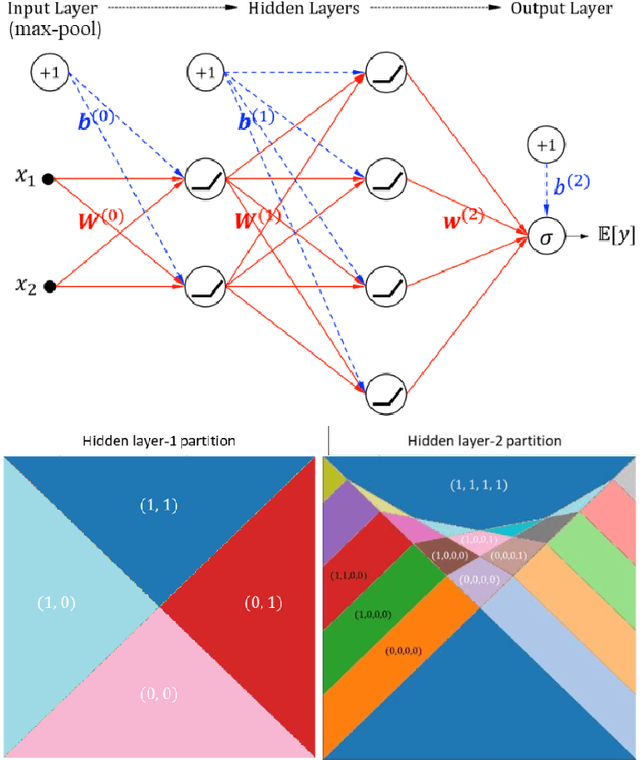
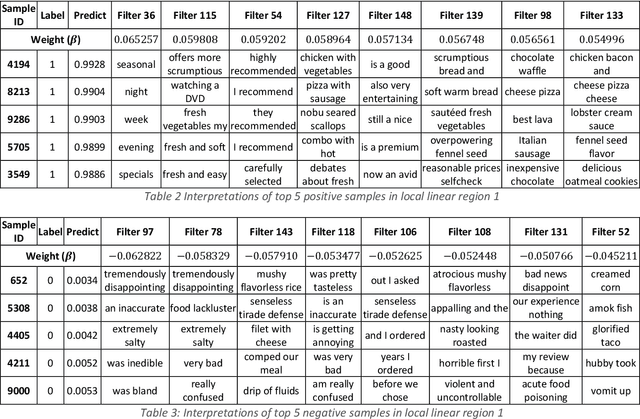
Deep learning models for natural language processing (NLP) are inherently complex and often viewed as black box in nature. This paper develops an approach for interpreting convolutional neural networks for text classification problems by exploiting the local-linear models inherent in ReLU-DNNs. The CNN model combines the word embedding through convolutional layers, filters them using max-pooling, and optimizes using a ReLU-DNN for classification. To get an overall self-interpretable model, the system of local linear models from the ReLU DNN are mapped back through the max-pool filter to the appropriate n-grams. Our results on experimental datasets demonstrate that our proposed technique produce parsimonious models that are self-interpretable and have comparable performance with respect to a more complex CNN model. We also study the impact of the complexity of the convolutional layers and the classification layers on the model performance.

Robustness Tests of NLP Machine Learning Models: Search and Semantically Replace

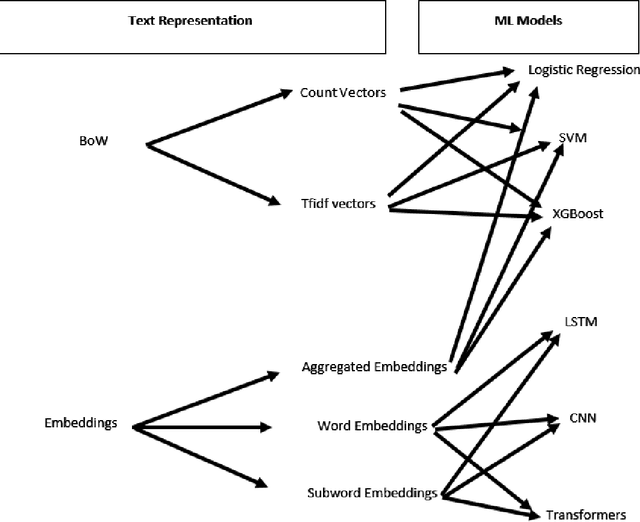
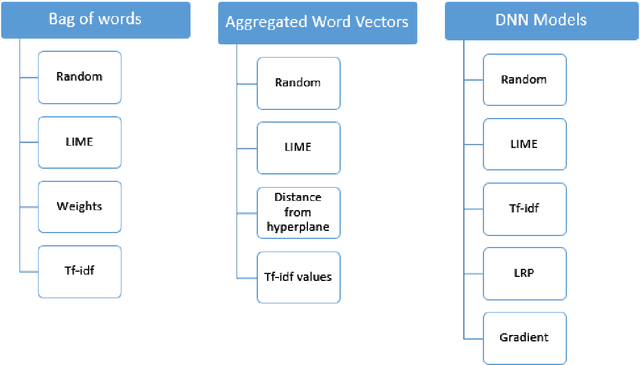
This paper proposes a strategy to assess the robustness of different machine learning models that involve natural language processing (NLP). The overall approach relies upon a Search and Semantically Replace strategy that consists of two steps: (1) Search, which identifies important parts in the text; (2) Semantically Replace, which finds replacements for the important parts, and constrains the replaced tokens with semantically similar words. We introduce different types of Search and Semantically Replace methods designed specifically for particular types of machine learning models. We also investigate the effectiveness of this strategy and provide a general framework to assess a variety of machine learning models. Finally, an empirical comparison is provided of robustness performance among three different model types, each with a different text representation.

Debiased Kernel Methods

I propose a practical procedure based on bias correction and sample splitting to calculate confidence intervals for functionals of generic kernel methods, i.e. nonparametric estimators learned in a reproducing kernel Hilbert space (RKHS). For example, an analyst may desire confidence intervals for functionals of kernel ridge regression or kernel instrumental variable regression. The framework encompasses (i) evaluations over discrete domains, (ii) treatment effects of discrete treatments, and (iii) incremental treatment effects of continuous treatments. For the target quantity, whether it is (i)-(iii), I prove pointwise root-n consistency, Gaussian approximation, and semiparametric efficiency by finite sample arguments. I show that the classic assumptions of RKHS learning theory also imply inference.