Automatic Generation of Behavioral Test Cases For Natural Language Processing Using Clustering and Prompting

Recent work in behavioral testing for natural language processing (NLP) models, such as Checklist, is inspired by related paradigms in software engineering testing. They allow evaluation of general linguistic capabilities and domain understanding, hence can help evaluate conceptual soundness and identify model weaknesses. However, a major challenge is the creation of test cases. The current packages rely on semi-automated approach using manual development which requires domain expertise and can be time consuming. This paper introduces an automated approach to develop test cases by exploiting the power of large language models and statistical techniques. It clusters the text representations to carefully construct meaningful groups and then apply prompting techniques to automatically generate Minimal Functionality Tests (MFT). The well-known Amazon Reviews corpus is used to demonstrate our approach. We analyze the behavioral test profiles across four different classification algorithms and discuss the limitations and strengths of those models.

Adaptive Discretization-based Non-Episodic Reinforcement Learning in Metric Spaces

We study non-episodic Reinforcement Learning for Lipschitz MDPs in which state-action space is a metric space, and the transition kernel and rewards are Lipschitz functions. We develop computationally efficient UCB-based algorithm, $\textit{ZoRL-}\epsilon$ that adaptively discretizes the state-action space and show that their regret as compared with $\epsilon$-optimal policy is bounded as $\mathcal{O}(\epsilon^{-(2 d_\mathcal{S} + d^\epsilon_z + 1)}\log{(T)})$, where $d^\epsilon_z$ is the $\epsilon$-zooming dimension. In contrast, if one uses the vanilla $\textit{UCRL-}2$ on a fixed discretization of the MDP, the regret w.r.t. a $\epsilon$-optimal policy scales as $\mathcal{O}(\epsilon^{-(2 d_\mathcal{S} + d + 1)}\log{(T)})$ so that the adaptivity gains are huge when $d^\epsilon_z \ll d$. Note that the absolute regret of any 'uniformly good' algorithm for a large family of continuous MDPs asymptotically scales as at least $\Omega(\log{(T)})$. Though adaptive discretization has been shown to yield $\mathcal{\tilde{O}}(H^{2.5}K^\frac{d_z + 1}{d_z + 2})$ regret in episodic RL, an attempt to extend this to the non-episodic case by employing constant duration episodes whose duration increases with $T$, is futile since $d_z \to d$ as $T \to \infty$. The current work shows how to obtain adaptivity gains for non-episodic RL. The theoretical results are supported by simulations on two systems where the performance of $\textit{ZoRL-}\epsilon$ is compared with that of '$\textit{UCRL-C}$,' the fixed discretization-based extension of $\textit{UCRL-}2$ for systems with continuous state-action spaces.

On Learning for Ambiguous Chance Constrained Problems

We study chance constrained optimization problems $\min_x f(x)$ s.t. $P(\left\{ \theta: g(x,\theta)\le 0 \right\})\ge 1-\epsilon$ where $\epsilon\in (0,1)$ is the violation probability, when the distribution $P$ is not known to the decision maker (DM). When the DM has access to a set of distributions $\mathcal{U}$ such that $P$ is contained in $\mathcal{U}$, then the problem is known as the ambiguous chance-constrained problem \cite{erdougan2006ambiguous}. We study ambiguous chance-constrained problem for the case when $\mathcal{U}$ is of the form $\left\{\mu:\frac{\mu (y)}{\nu(y)}\leq C, \forall y\in\Theta, \mu(y)\ge 0\right\}$, where $\nu$ is a ``reference distribution.'' We show that in this case the original problem can be ``well-approximated'' by a sampled problem in which $N$ i.i.d. samples of $\theta$ are drawn from $\nu$, and the original constraint is replaced with $g(x,\theta_i)\le 0,~i=1,2,\ldots,N$. We also derive the sample complexity associated with this approximation, i.e., for $\epsilon,\delta>0$ the number of samples which must be drawn from $\nu$ so that with a probability greater than $1-\delta$ (over the randomness of $\nu$), the solution obtained by solving the sampled program yields an $\epsilon$-feasible solution for the original chance constrained problem.

Related Rhythms: Recommendation System To Discover Music You May Like

Machine Learning models are being utilized extensively to drive recommender systems, which is a widely explored topic today. This is especially true of the music industry, where we are witnessing a surge in growth. Besides a large chunk of active users, these systems are fueled by massive amounts of data. These large-scale systems yield applications that aim to provide a better user experience and to keep customers actively engaged. In this paper, a distributed Machine Learning (ML) pipeline is delineated, which is capable of taking a subset of songs as input and producing a new subset of songs identified as being similar to the inputted subset. The publicly accessible Million Songs Dataset (MSD) enables researchers to develop and explore reasonably efficient systems for audio track analysis and recommendations, without having to access a commercialized music platform. The objective of the proposed application is to leverage an ML system trained to optimally recommend songs that a user might like.

Finite Time Regret Bounds for Minimum Variance Control of Autoregressive Systems with Exogenous Inputs

Minimum variance controllers have been employed in a wide-range of industrial applications. A key challenge experienced by many adaptive controllers is their poor empirical performance in the initial stages of learning. In this paper, we address the problem of initializing them so that they provide acceptable transients, and also provide an accompanying finite-time regret analysis, for adaptive minimum variance control of an auto-regressive system with exogenous inputs (ARX). Following [3], we consider a modified version of the Certainty Equivalence (CE) adaptive controller, which we call PIECE, that utilizes probing inputs for exploration. We show that it has a $C \log T$ bound on the regret after $T$ time-steps for bounded noise, and $C\log^2 T$ in the case of sub-Gaussian noise. The simulation results demonstrate the advantage of PIECE over the algorithm proposed in [3] as well as the standard Certainty Equivalence controller especially in the initial learning phase. To the best of our knowledge, this is the first work that provides finite-time regret bounds for an adaptive minimum variance controller.

Kernel Ridge Regression Inference

We provide uniform confidence bands for kernel ridge regression (KRR), with finite sample guarantees. KRR is ubiquitous, yet--to our knowledge--this paper supplies the first exact, uniform confidence bands for KRR in the non-parametric regime where the regularization parameter $\lambda$ converges to 0, for general data distributions. Our proposed uniform confidence band is based on a new, symmetrized multiplier bootstrap procedure with a closed form solution, which allows for valid uncertainty quantification without assumptions on the bias. To justify the procedure, we derive non-asymptotic, uniform Gaussian and bootstrap couplings for partial sums in a reproducing kernel Hilbert space (RKHS) with bounded kernel. Our results imply strong approximation for empirical processes indexed by the RKHS unit ball, with sharp, logarithmic dependence on the covering number.

Signed Graph Neural Networks: A Frequency Perspective

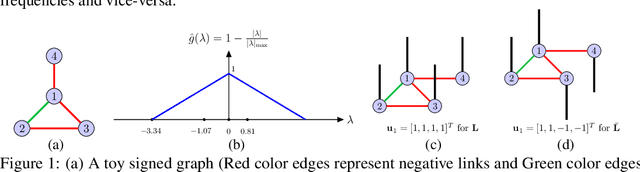
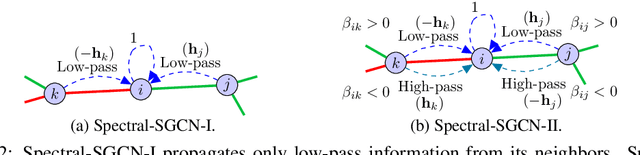
Graph convolutional networks (GCNs) and its variants are designed for unsigned graphs containing only positive links. Many existing GCNs have been derived from the spectral domain analysis of signals lying over (unsigned) graphs and in each convolution layer they perform low-pass filtering of the input features followed by a learnable linear transformation. Their extension to signed graphs with positive as well as negative links imposes multiple issues including computational irregularities and ambiguous frequency interpretation, making the design of computationally efficient low pass filters challenging. In this paper, we address these issues via spectral analysis of signed graphs and propose two different signed graph neural networks, one keeps only low-frequency information and one also retains high-frequency information. We further introduce magnetic signed Laplacian and use its eigendecomposition for spectral analysis of directed signed graphs. We test our methods for node classification and link sign prediction tasks on signed graphs and achieve state-of-the-art performances.

Quantifying Inherent Randomness in Machine Learning Algorithms

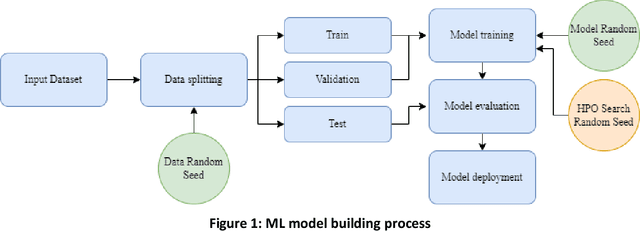
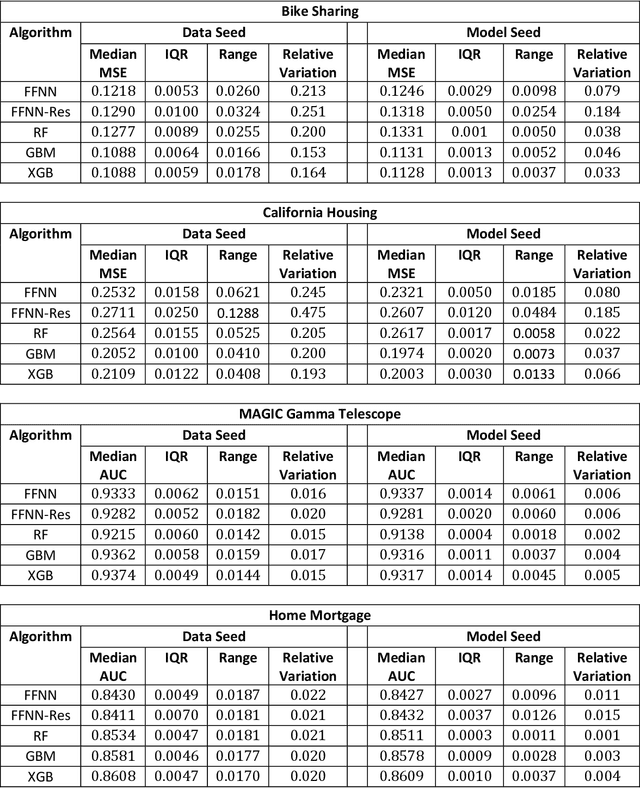
Most machine learning (ML) algorithms have several stochastic elements, and their performances are affected by these sources of randomness. This paper uses an empirical study to systematically examine the effects of two sources: randomness in model training and randomness in the partitioning of a dataset into training and test subsets. We quantify and compare the magnitude of the variation in predictive performance for the following ML algorithms: Random Forests (RFs), Gradient Boosting Machines (GBMs), and Feedforward Neural Networks (FFNNs). Among the different algorithms, randomness in model training causes larger variation for FFNNs compared to tree-based methods. This is to be expected as FFNNs have more stochastic elements that are part of their model initialization and training. We also found that random splitting of datasets leads to higher variation compared to the inherent randomness from model training. The variation from data splitting can be a major issue if the original dataset has considerable heterogeneity. Keywords: Model Training, Reproducibility, Variation

Understanding Metrics for Paraphrasing

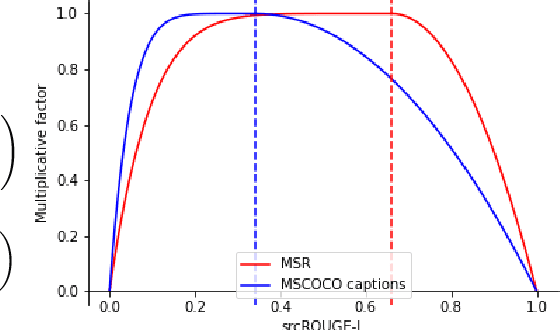
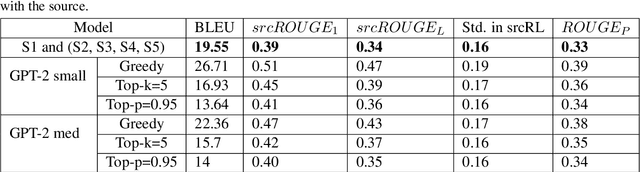
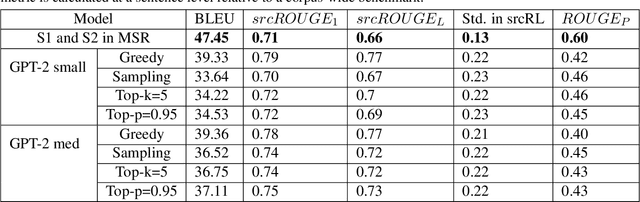
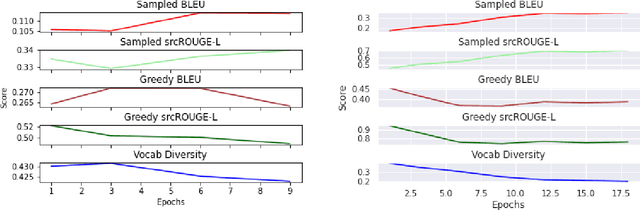
Paraphrase generation is a difficult problem. This is not only because of the limitations in text generation capabilities but also due that to the lack of a proper definition of what qualifies as a paraphrase and corresponding metrics to measure how good it is. Metrics for evaluation of paraphrasing quality is an on going research problem. Most of the existing metrics in use having been borrowed from other tasks do not capture the complete essence of a good paraphrase, and often fail at borderline-cases. In this work, we propose a novel metric $ROUGE_P$ to measure the quality of paraphrases along the dimensions of adequacy, novelty and fluency. We also provide empirical evidence to show that the current natural language generation metrics are insufficient to measure these desired properties of a good paraphrase. We look at paraphrase model fine-tuning and generation from the lens of metrics to gain a deeper understanding of what it takes to generate and evaluate a good paraphrase.

Automatic Debiased Machine Learning for Dynamic Treatment Effects

We extend the idea of automated debiased machine learning to the dynamic treatment regime. We show that the multiply robust formula for the dynamic treatment regime with discrete treatments can be re-stated in terms of a recursive Riesz representer characterization of nested mean regressions. We then apply a recursive Riesz representer estimation learning algorithm that estimates de-biasing corrections without the need to characterize how the correction terms look like, such as for instance, products of inverse probability weighting terms, as is done in prior work on doubly robust estimation in the dynamic regime. Our approach defines a sequence of loss minimization problems, whose minimizers are the mulitpliers of the de-biasing correction, hence circumventing the need for solving auxiliary propensity models and directly optimizing for the mean squared error of the target de-biasing correction.