An Optimization Framework for Differentially Private Sparse Fine-Tuning

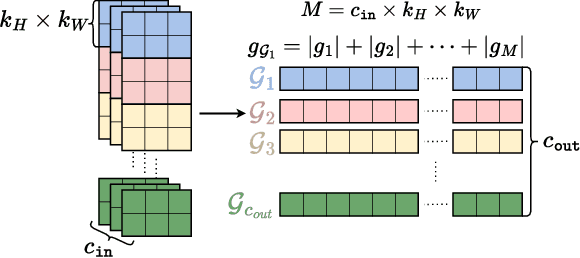
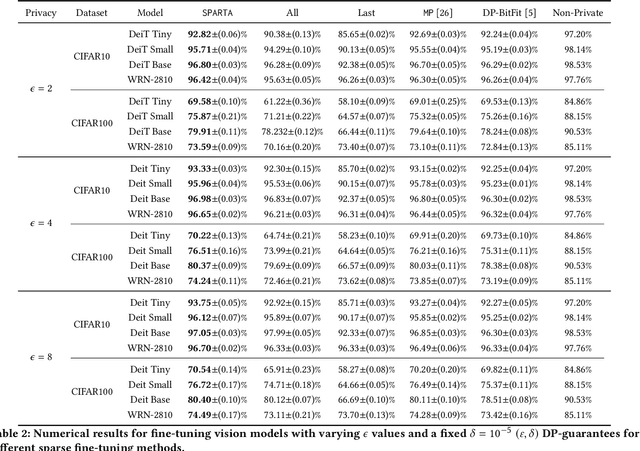
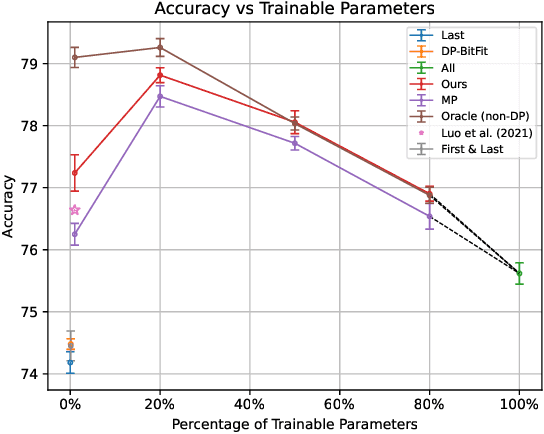
Differentially private stochastic gradient descent (DP-SGD) is broadly considered to be the gold standard for training and fine-tuning neural networks under differential privacy (DP). With the increasing availability of high-quality pre-trained model checkpoints (e.g., vision and language models), fine-tuning has become a popular strategy. However, despite recent progress in understanding and applying DP-SGD for private transfer learning tasks, significant challenges remain -- most notably, the performance gap between models fine-tuned with DP-SGD and their non-private counterparts. Sparse fine-tuning on private data has emerged as an alternative to full-model fine-tuning; recent work has shown that privately fine-tuning only a small subset of model weights and keeping the rest of the weights fixed can lead to better performance. In this work, we propose a new approach for sparse fine-tuning of neural networks under DP. Existing work on private sparse finetuning often used fixed choice of trainable weights (e.g., updating only the last layer), or relied on public model's weights to choose the subset of weights to modify. Such choice of weights remains suboptimal. In contrast, we explore an optimization-based approach, where our selection method makes use of the private gradient information, while using off the shelf privacy accounting techniques. Our numerical experiments on several computer vision models and datasets show that our selection method leads to better prediction accuracy, compared to full-model private fine-tuning or existing private sparse fine-tuning approaches.

Efficient AI in Practice: Training and Deployment of Efficient LLMs for Industry Applications

Large language models (LLMs) have demonstrated remarkable performance across a wide range of industrial applications, from search and recommendations to generative tasks. Although scaling laws indicate that larger models generally yield better generalization and performance, their substantial computational requirements often render them impractical for many real-world scenarios at scale. In this paper, we present methods and insights for training small language models (SLMs) that deliver high performance and efficiency in deployment. We focus on two key techniques: (1) knowledge distillation and (2) model compression via quantization and pruning. These approaches enable SLMs to retain much of the quality of their larger counterparts while significantly reducing training, serving costs, and latency. We detail the impact of these techniques on a variety of use cases at a large professional social network platform and share deployment lessons - including hardware optimization strategies that enhance speed and throughput for both predictive and reasoning-based applications.

HASSLE-free: A unified Framework for Sparse plus Low-Rank Matrix Decomposition for LLMs

The impressive capabilities of large foundation models come at a cost of substantial computing resources to serve them. Compressing these pre-trained models is of practical interest as it can democratize deploying them to the machine learning community at large by lowering the costs associated with inference. A promising compression scheme is to decompose foundation models' dense weights into a sum of sparse plus low-rank matrices. In this paper, we design a unified framework coined HASSLE-free for (semi-structured) sparse plus low-rank matrix decomposition of foundation models. Our framework introduces the local layer-wise reconstruction error objective for this decomposition, we demonstrate that prior work solves a relaxation of this optimization problem; and we provide efficient and scalable methods to minimize the exact introduced optimization problem. HASSLE-free substantially outperforms state-of-the-art methods in terms of the introduced objective and a wide range of LLM evaluation benchmarks. For the Llama3-8B model with a 2:4 sparsity component plus a 64-rank component decomposition, a compression scheme for which recent work shows important inference acceleration on GPUs, HASSLE-free reduces the test perplexity by 12% for the WikiText-2 dataset and reduces the gap (compared to the dense model) of the average of eight popular zero-shot tasks by 15% compared to existing methods.

Efficient user history modeling with amortized inference for deep learning recommendation models

We study user history modeling via Transformer encoders in deep learning recommendation models (DLRM). Such architectures can significantly improve recommendation quality, but usually incur high latency cost necessitating infrastructure upgrades or very small Transformer models. An important part of user history modeling is early fusion of the candidate item and various methods have been studied. We revisit early fusion and compare concatenation of the candidate to each history item against appending it to the end of the list as a separate item. Using the latter method, allows us to reformulate the recently proposed amortized history inference algorithm M-FALCON \cite{zhai2024actions} for the case of DLRM models. We show via experimental results that appending with cross-attention performs on par with concatenation and that amortization significantly reduces inference costs. We conclude with results from deploying this model on the LinkedIn Feed and Ads surfaces, where amortization reduces latency by 30\% compared to non-amortized inference.

Preserving Deep Representations In One-Shot Pruning: A Hessian-Free Second-Order Optimization Framework

We present SNOWS, a one-shot post-training pruning framework aimed at reducing the cost of vision network inference without retraining. Current leading one-shot pruning methods minimize layer-wise least squares reconstruction error which does not take into account deeper network representations. We propose to optimize a more global reconstruction objective. This objective accounts for nonlinear activations deep in the network to obtain a better proxy for the network loss. This nonlinear objective leads to a more challenging optimization problem -- we demonstrate it can be solved efficiently using a specialized second-order optimization framework. A key innovation of our framework is the use of Hessian-free optimization to compute exact Newton descent steps without needing to compute or store the full Hessian matrix. A distinct advantage of SNOWS is that it can be readily applied on top of any sparse mask derived from prior methods, readjusting their weights to exploit nonlinearities in deep feature representations. SNOWS obtains state-of-the-art results on various one-shot pruning benchmarks including residual networks and Vision Transformers (ViT/B-16 and ViT/L-16, 86m and 304m parameters respectively).

ALPS: Improved Optimization for Highly Sparse One-Shot Pruning for Large Language Models

The impressive performance of Large Language Models (LLMs) across various natural language processing tasks comes at the cost of vast computational resources and storage requirements. One-shot pruning techniques offer a way to alleviate these burdens by removing redundant weights without the need for retraining. Yet, the massive scale of LLMs often forces current pruning approaches to rely on heuristics instead of optimization-based techniques, potentially resulting in suboptimal compression. In this paper, we introduce ALPS, an optimization-based framework that tackles the pruning problem using the operator splitting technique and a preconditioned conjugate gradient-based post-processing step. Our approach incorporates novel techniques to accelerate and theoretically guarantee convergence while leveraging vectorization and GPU parallelism for efficiency. ALPS substantially outperforms state-of-the-art methods in terms of the pruning objective and perplexity reduction, particularly for highly sparse models. On the OPT-30B model with 70% sparsity, ALPS achieves a 13% reduction in test perplexity on the WikiText dataset and a 19% improvement in zero-shot benchmark performance compared to existing methods.

FALCON: FLOP-Aware Combinatorial Optimization for Neural Network Pruning

The increasing computational demands of modern neural networks present deployment challenges on resource-constrained devices. Network pruning offers a solution to reduce model size and computational cost while maintaining performance. However, most current pruning methods focus primarily on improving sparsity by reducing the number of nonzero parameters, often neglecting other deployment costs such as inference time, which are closely related to the number of floating-point operations (FLOPs). In this paper, we propose FALCON, a novel combinatorial-optimization-based framework for network pruning that jointly takes into account model accuracy (fidelity), FLOPs, and sparsity constraints. A main building block of our approach is an integer linear program (ILP) that simultaneously handles FLOP and sparsity constraints. We present a novel algorithm to approximately solve the ILP. We propose a novel first-order method for our optimization framework which makes use of our ILP solver. Using problem structure (e.g., the low-rank structure of approx. Hessian), we can address instances with millions of parameters. Our experiments demonstrate that FALCON achieves superior accuracy compared to other pruning approaches within a fixed FLOP budget. For instance, for ResNet50 with 20% of the total FLOPs retained, our approach improves the accuracy by 48% relative to state-of-the-art. Furthermore, in gradual pruning settings with re-training between pruning steps, our framework outperforms existing pruning methods, emphasizing the significance of incorporating both FLOP and sparsity constraints for effective network pruning.

Randomization Can Reduce Both Bias and Variance: A Case Study in Random Forests

We study the often overlooked phenomenon, first noted in \cite{breiman2001random}, that random forests appear to reduce bias compared to bagging. Motivated by an interesting paper by \cite{mentch2020randomization}, where the authors argue that random forests reduce effective degrees of freedom and only outperform bagging ensembles in low signal-to-noise ratio (SNR) settings, we explore how random forests can uncover patterns in the data missed by bagging. We empirically demonstrate that in the presence of such patterns, random forests reduce bias along with variance and increasingly outperform bagging ensembles when SNR is high. Our observations offer insights into the real-world success of random forests across a range of SNRs and enhance our understanding of the difference between random forests and bagging ensembles with respect to the randomization injected into each split. Our investigations also yield practical insights into the importance of tuning $mtry$ in random forests.

FAST: An Optimization Framework for Fast Additive Segmentation in Transparent ML

We present FAST, an optimization framework for fast additive segmentation. FAST segments piecewise constant shape functions for each feature in a dataset to produce transparent additive models. The framework leverages a novel optimization procedure to fit these models $\sim$2 orders of magnitude faster than existing state-of-the-art methods, such as explainable boosting machines \citep{nori2019interpretml}. We also develop new feature selection algorithms in the FAST framework to fit parsimonious models that perform well. Through experiments and case studies, we show that FAST improves the computational efficiency and interpretability of additive models.

FFSplit: Split Feed-Forward Network For Optimizing Accuracy-Efficiency Trade-off in Language Model Inference

The large number of parameters in Pretrained Language Models enhance their performance, but also make them resource-intensive, making it challenging to deploy them on commodity hardware like a single GPU. Due to the memory and power limitations of these devices, model compression techniques are often used to decrease both the model's size and its inference latency. This usually results in a trade-off between model accuracy and efficiency. Therefore, optimizing this balance is essential for effectively deploying LLMs on commodity hardware. A significant portion of the efficiency challenge is the Feed-forward network (FFN) component, which accounts for roughly $\frac{2}{3}$ total parameters and inference latency. In this paper, we first observe that only a few neurons of FFN module have large output norm for any input tokens, a.k.a. heavy hitters, while the others are sparsely triggered by different tokens. Based on this observation, we explicitly split the FFN into two parts according to the heavy hitters. We improve the efficiency-accuracy trade-off of existing compression methods by allocating more resource to FFN parts with heavy hitters. In practice, our method can reduce model size by 43.1\% and bring $1.25\sim1.56\times$ wall clock time speedup on different hardware with negligible accuracy drop.