On the Stability of Iterative Retraining of Generative Models on their own Data

Deep generative models have made tremendous progress in modeling complex data, often exhibiting generation quality that surpasses a typical human's ability to discern the authenticity of samples. Undeniably, a key driver of this success is enabled by the massive amounts of web-scale data consumed by these models. Due to these models' striking performance and ease of availability, the web will inevitably be increasingly populated with synthetic content. Such a fact directly implies that future iterations of generative models must contend with the reality that their training is curated from both clean data and artificially generated data from past models. In this paper, we develop a framework to rigorously study the impact of training generative models on mixed datasets (of real and synthetic data) on their stability. We first prove the stability of iterative training under the condition that the initial generative models approximate the data distribution well enough and the proportion of clean training data (w.r.t. synthetic data) is large enough. We empirically validate our theory on both synthetic and natural images by iteratively training normalizing flows and state-of-the-art diffusion models on CIFAR10 and FFHQ.

Omega: Optimistic EMA Gradients

Stochastic min-max optimization has gained interest in the machine learning community with the advancements in GANs and adversarial training. Although game optimization is fairly well understood in the deterministic setting, some issues persist in the stochastic regime. Recent work has shown that stochastic gradient descent-ascent methods such as the optimistic gradient are highly sensitive to noise or can fail to converge. Although alternative strategies exist, they can be prohibitively expensive. We introduce Omega, a method with optimistic-like updates that mitigates the impact of noise by incorporating an EMA of historic gradients in its update rule. We also explore a variation of this algorithm that incorporates momentum. Although we do not provide convergence guarantees, our experiments on stochastic games show that Omega outperforms the optimistic gradient method when applied to linear players.

Synergies Between Disentanglement and Sparsity: a Multi-Task Learning Perspective

Although disentangled representations are often said to be beneficial for downstream tasks, current empirical and theoretical understanding is limited. In this work, we provide evidence that disentangled representations coupled with sparse base-predictors improve generalization. In the context of multi-task learning, we prove a new identifiability result that provides conditions under which maximally sparse base-predictors yield disentangled representations. Motivated by this theoretical result, we propose a practical approach to learn disentangled representations based on a sparsity-promoting bi-level optimization problem. Finally, we explore a meta-learning version of this algorithm based on group Lasso multiclass SVM base-predictors, for which we derive a tractable dual formulation. It obtains competitive results on standard few-shot classification benchmarks, while each task is using only a fraction of the learned representations.

The Curse of Unrolling: Rate of Differentiating Through Optimization

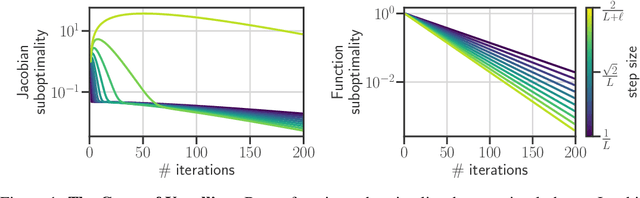
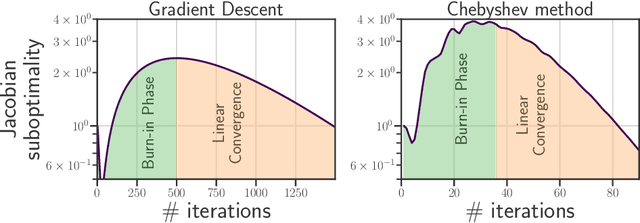
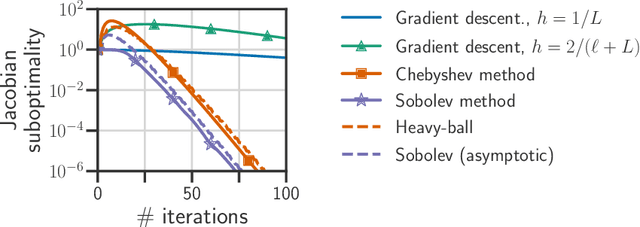
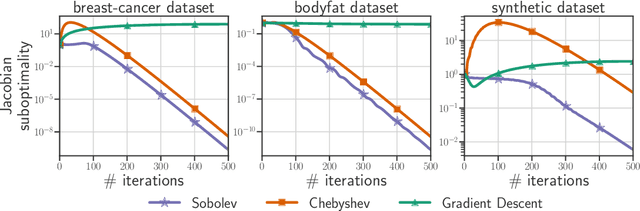
Computing the Jacobian of the solution of an optimization problem is a central problem in machine learning, with applications in hyperparameter optimization, meta-learning, optimization as a layer, and dataset distillation, to name a few. Unrolled differentiation is a popular heuristic that approximates the solution using an iterative solver and differentiates it through the computational path. This work provides a non-asymptotic convergence-rate analysis of this approach on quadratic objectives for gradient descent and the Chebyshev method. We show that to ensure convergence of the Jacobian, we can either 1) choose a large learning rate leading to a fast asymptotic convergence but accept that the algorithm may have an arbitrarily long burn-in phase or 2) choose a smaller learning rate leading to an immediate but slower convergence. We refer to this phenomenon as the curse of unrolling. Finally, we discuss open problems relative to this approach, such as deriving a practical update rule for the optimal unrolling strategy and making novel connections with the field of Sobolev orthogonal polynomials.

On the Limitations of Elo: Real-World Games, are Transitive, not Additive

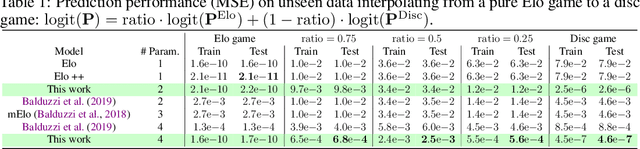
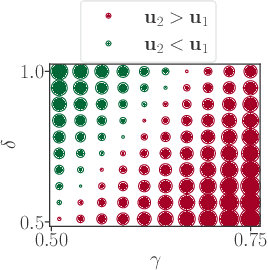
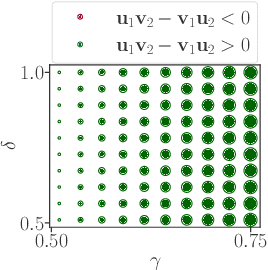
Real-world competitive games, such as chess, go, or StarCraft II, rely on Elo models to measure the strength of their players. Since these games are not fully transitive, using Elo implicitly assumes they have a strong transitive component that can correctly be identified and extracted. In this study, we investigate the challenge of identifying the strength of the transitive component in games. First, we show that Elo models can fail to extract this transitive component, even in elementary transitive games. Then, based on this observation, we propose an extension of the Elo score: we end up with a disc ranking system that assigns each player two scores, which we refer to as skill and consistency. Finally, we propose an empirical validation on payoff matrices coming from real-world games played by bots and humans.

Beyond L1: Faster and Better Sparse Models with skglm

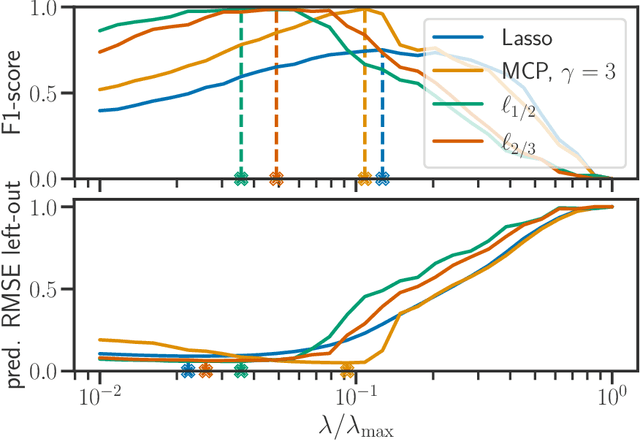
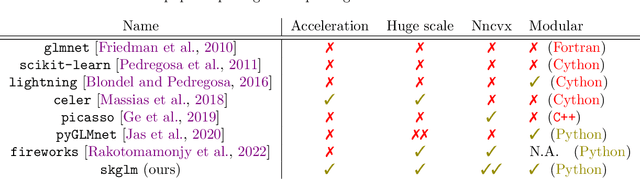
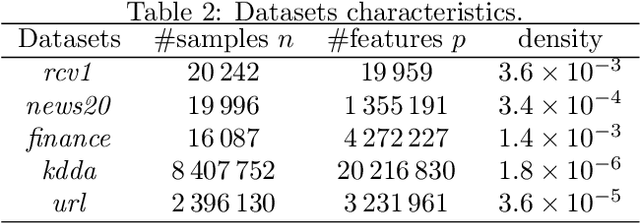
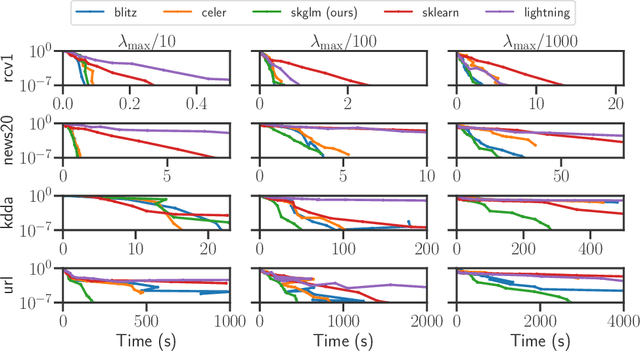
We propose a new fast algorithm to estimate any sparse generalized linear model with convex or non-convex separable penalties. Our algorithm is able to solve problems with millions of samples and features in seconds, by relying on coordinate descent, working sets and Anderson acceleration. It handles previously unaddressed models, and is extensively shown to improve state-of-art algorithms. We provide a flexible, scikit-learn compatible package, which easily handles customized datafits and penalties.

Implicit differentiation for fast hyperparameter selection in non-smooth convex learning

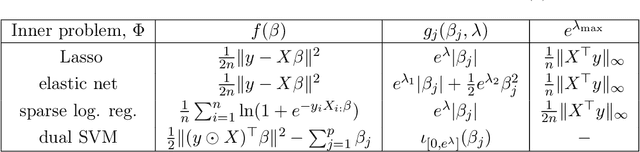
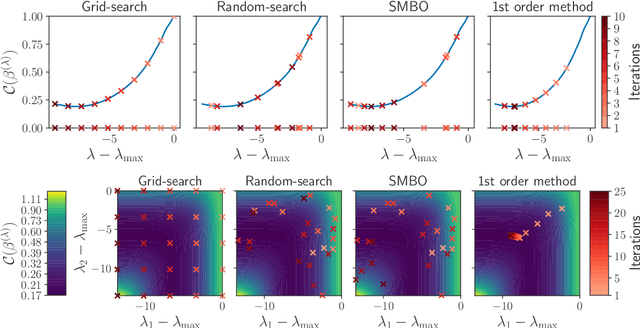
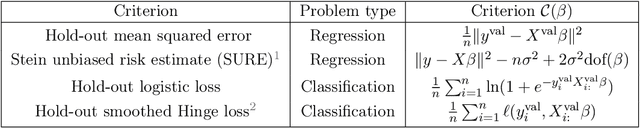
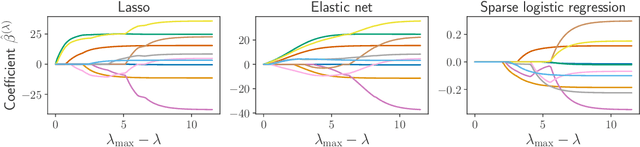
Finding the optimal hyperparameters of a model can be cast as a bilevel optimization problem, typically solved using zero-order techniques. In this work we study first-order methods when the inner optimization problem is convex but non-smooth. We show that the forward-mode differentiation of proximal gradient descent and proximal coordinate descent yield sequences of Jacobians converging toward the exact Jacobian. Using implicit differentiation, we show it is possible to leverage the non-smoothness of the inner problem to speed up the computation. Finally, we provide a bound on the error made on the hypergradient when the inner optimization problem is solved approximately. Results on regression and classification problems reveal computational benefits for hyperparameter optimization, especially when multiple hyperparameters are required.

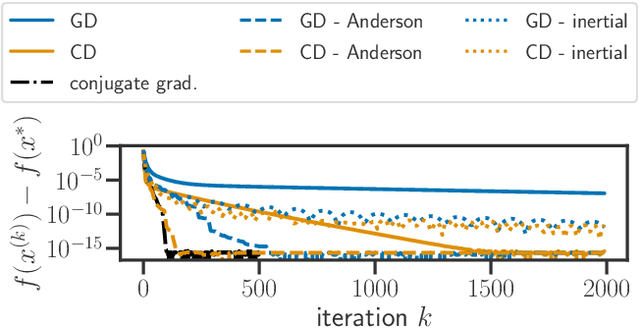
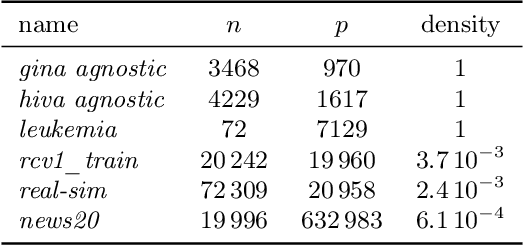
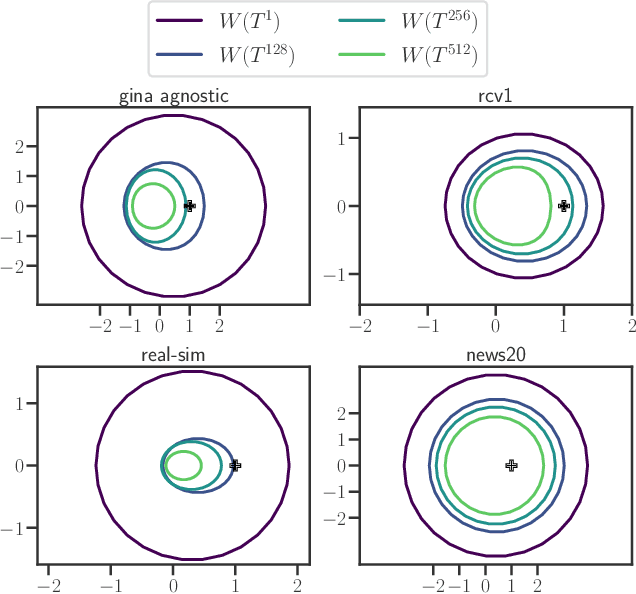
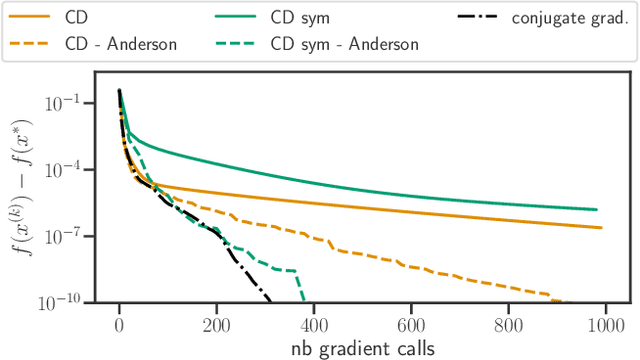
Anderson acceleration of coordinate descent

Acceleration of first order methods is mainly obtained via inertial techniques \`a la Nesterov, or via nonlinear extrapolation. The latter has known a recent surge of interest, with successful applications to gradient and proximal gradient techniques. On multiple Machine Learning problems, coordinate descent achieves performance significantly superior to full-gradient methods. Speeding up coordinate descent in practice is not easy: inertially accelerated versions of coordinate descent are theoretically accelerated, but might not always lead to practical speed-ups. We propose an accelerated version of coordinate descent using extrapolation, showing considerable speed up in practice, compared to inertial accelerated coordinate descent and extrapolated (proximal) gradient descent. Experiments on least squares, Lasso, elastic net and logistic regression validate the approach.

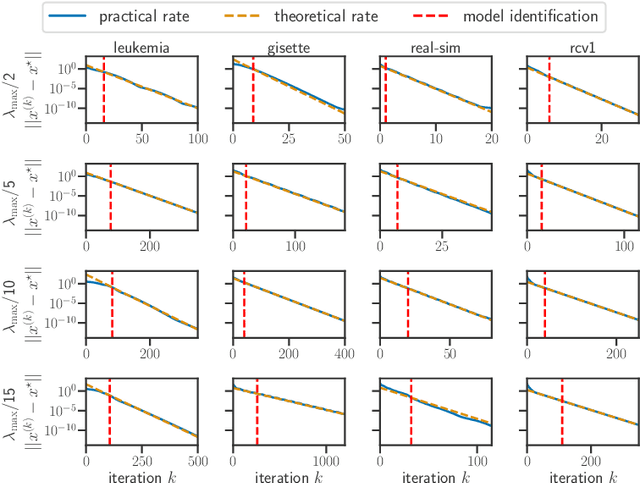
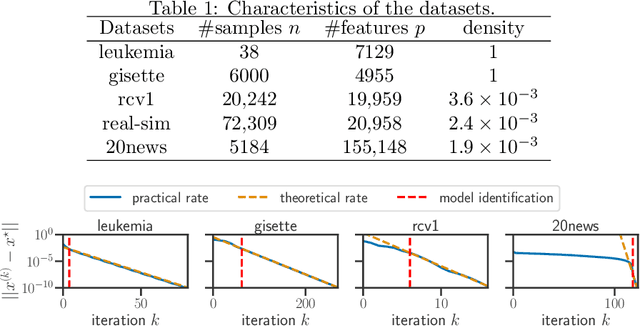
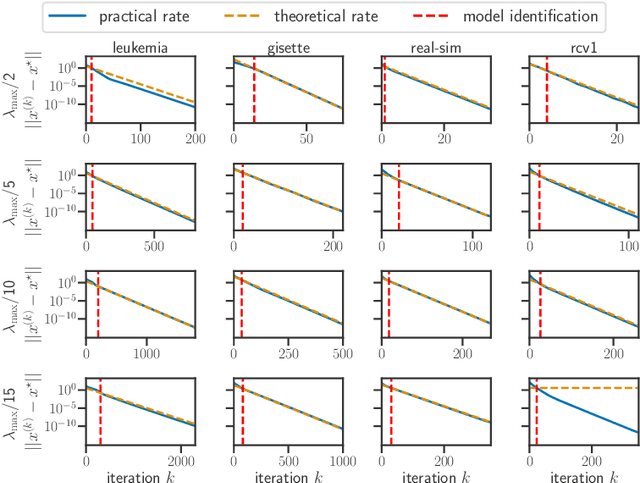
Model identification and local linear convergence of coordinate descent

For composite nonsmooth optimization problems, Forward-Backward algorithm achieves model identification (e.g. support identification for the Lasso) after a finite number of iterations, provided the objective function is regular enough. Results concerning coordinate descent are scarcer and model identification has only been shown for specific estimators, the support-vector machine for instance. In this work, we show that cyclic coordinate descent achieves model identification in finite time for a wide class of functions. In addition, we prove explicit local linear convergence rates for coordinate descent. Extensive experiments on various estimators and on real datasets demonstrate that these rates match well empirical results.

Implicit differentiation of Lasso-type models for hyperparameter optimization

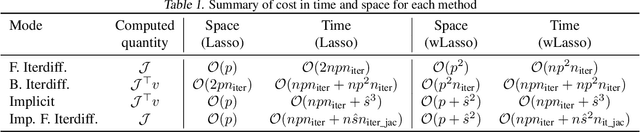
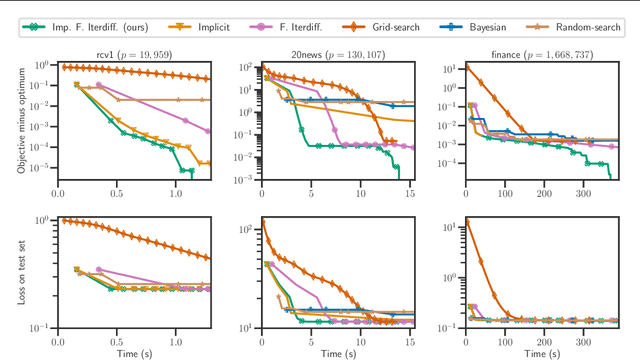
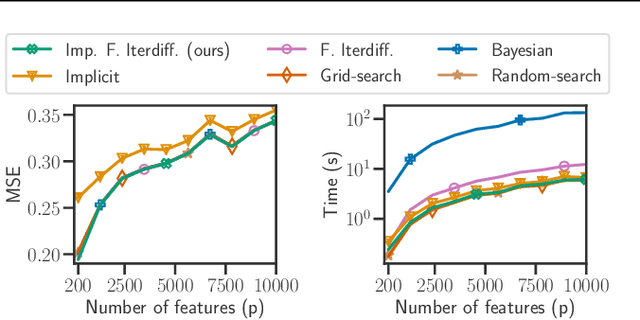
Setting regularization parameters for Lasso-type estimators is notoriously difficult, though crucial in practice. The most popular hyperparameter optimization approach is grid-search using held-out validation data. Grid-search however requires to choose a predefined grid for each parameter, which scales exponentially in the number of parameters. Another approach is to cast hyperparameter optimization as a bi-level optimization problem, one can solve by gradient descent. The key challenge for these methods is the estimation of the gradient with respect to the hyperparameters. Computing this gradient via forward or backward automatic differentiation is possible yet usually suffers from high memory consumption. Alternatively implicit differentiation typically involves solving a linear system which can be prohibitive and numerically unstable in high dimension. In addition, implicit differentiation usually assumes smooth loss functions, which is not the case for Lasso-type problems. This work introduces an efficient implicit differentiation algorithm, without matrix inversion, tailored for Lasso-type problems. Our approach scales to high-dimensional data by leveraging the sparsity of the solutions. Experiments demonstrate that the proposed method outperforms a large number of standard methods to optimize the error on held-out data, or the Stein Unbiased Risk Estimator (SURE).