Reliable Critics: Monotonic Improvement and Convergence Guarantees for Reinforcement Learning

Despite decades of research, it remains challenging to correctly use Reinforcement Learning (RL) algorithms with function approximation. A prime example is policy iteration, whose fundamental guarantee of monotonic improvement collapses even under linear function approximation. To address this issue, we introduce Reliable Policy Iteration (RPI). It replaces the common projection or Bellman-error minimization during policy evaluation with a Bellman-based constrained optimization. We prove that not only does RPI confer textbook monotonicity on its value estimates but these estimates also lower bound the true return. Also, their limit partially satisfies the unprojected Bellman equation, emphasizing RPI's natural fit within RL. RPI is the first algorithm with such monotonicity and convergence guarantees under function approximation. For practical use, we provide a model-free variant of RPI that amounts to a novel critic. It can be readily integrated into primary model-free PI implementations such as DQN and DDPG. In classical control tasks, such RPI-enhanced variants consistently maintain their lower-bound guarantee while matching or surpassing the performance of all baseline methods.

Reinforcement Learning with Quasi-Hyperbolic Discounting

Reinforcement learning has traditionally been studied with exponential discounting or the average reward setup, mainly due to their mathematical tractability. However, such frameworks fall short of accurately capturing human behavior, which has a bias towards immediate gratification. Quasi-Hyperbolic (QH) discounting is a simple alternative for modeling this bias. Unlike in traditional discounting, though, the optimal QH-policy, starting from some time $t_1,$ can be different to the one starting from $t_2.$ Hence, the future self of an agent, if it is naive or impatient, can deviate from the policy that is optimal at the start, leading to sub-optimal overall returns. To prevent this behavior, an alternative is to work with a policy anchored in a Markov Perfect Equilibrium (MPE). In this work, we propose the first model-free algorithm for finding an MPE. Using a two-timescale analysis, we show that, if our algorithm converges, then the limit must be an MPE. We also validate this claim numerically for the standard inventory system with stochastic demands. Our work significantly advances the practical application of reinforcement learning.

Online Learning of Weakly Coupled MDP Policies for Load Balancing and Auto Scaling

Load balancing and auto scaling are at the core of scalable, contemporary systems, addressing dynamic resource allocation and service rate adjustments in response to workload changes. This paper introduces a novel model and algorithms for tuning load balancers coupled with auto scalers, considering bursty traffic arriving at finite queues. We begin by presenting the problem as a weakly coupled Markov Decision Processes (MDP), solvable via a linear program (LP). However, as the number of control variables of such LP grows combinatorially, we introduce a more tractable relaxed LP formulation, and extend it to tackle the problem of online parameter learning and policy optimization using a two-timescale algorithm based on the LP Lagrangian.

Global Convergence Guarantees for Federated Policy Gradient Methods with Adversaries

Federated Reinforcement Learning (FRL) allows multiple agents to collaboratively build a decision making policy without sharing raw trajectories. However, if a small fraction of these agents are adversarial, it can lead to catastrophic results. We propose a policy gradient based approach that is robust to adversarial agents which can send arbitrary values to the server. Under this setting, our results form the first global convergence guarantees with general parametrization. These results demonstrate resilience with adversaries, while achieving sample complexity of order $\tilde{\mathcal{O}}\left( \frac{1}{\epsilon^2} \left( \frac{1}{N-f} + \frac{f^2}{(N-f)^2}\right)\right)$, where $N$ is the total number of agents and $f$ is the number of adversarial agents.

VaR\ and CVaR Estimation in a Markov Cost Process: Lower and Upper Bounds

We tackle the problem of estimating the Value-at-Risk (VaR) and the Conditional Value-at-Risk (CVaR) of the infinite-horizon discounted cost within a Markov cost process. First, we derive a minimax lower bound of $\Omega(1/\sqrt{n})$ that holds both in an expected and in a probabilistic sense. Then, using a finite-horizon truncation scheme, we derive an upper bound for the error in CVaR estimation, which matches our lower bound up to constant factors. Finally, we discuss an extension of our estimation scheme that covers more general risk measures satisfying a certain continuity criterion, e.g., spectral risk measures, utility-based shortfall risk. To the best of our knowledge, our work is the first to provide lower and upper bounds on the estimation error for any risk measure within Markovian settings. We remark that our lower bounds also extend to the infinite-horizon discounted costs' mean. Even in that case, our result $\Omega(1/\sqrt{n}) $ improves upon the existing result $\Omega(1/n)$[13].

Online Learning with Adversaries: A Differential Inclusion Analysis

We consider the measurement model $Y = AX,$ where $X$ and, hence, $Y$ are random variables and $A$ is an a priori known tall matrix. At each time instance, a sample of one of $Y$'s coordinates is available, and the goal is to estimate $\mu := \mathbb{E}[X]$ via these samples. However, the challenge is that a small but unknown subset of $Y$'s coordinates are controlled by adversaries with infinite power: they can return any real number each time they are queried for a sample. For such an adversarial setting, we propose the first asynchronous online algorithm that converges to $\mu$ almost surely. We prove this result using a novel differential inclusion based two-timescale analysis. Two key highlights of our proof include: (a) the use of a novel Lyapunov function for showing that $\mu$ is the unique global attractor for our algorithm's limiting dynamics, and (b) the use of martingale and stopping time theory to show that our algorithm's iterates are almost surely bounded.

SoftTreeMax: Exponential Variance Reduction in Policy Gradient via Tree Search

Despite the popularity of policy gradient methods, they are known to suffer from large variance and high sample complexity. To mitigate this, we introduce SoftTreeMax -- a generalization of softmax that takes planning into account. In SoftTreeMax, we extend the traditional logits with the multi-step discounted cumulative reward, topped with the logits of future states. We consider two variants of SoftTreeMax, one for cumulative reward and one for exponentiated reward. For both, we analyze the gradient variance and reveal for the first time the role of a tree expansion policy in mitigating this variance. We prove that the resulting variance decays exponentially with the planning horizon as a function of the expansion policy. Specifically, we show that the closer the resulting state transitions are to uniform, the faster the decay. In a practical implementation, we utilize a parallelized GPU-based simulator for fast and efficient tree search. Our differentiable tree-based policy leverages all gradients at the tree leaves in each environment step instead of the traditional single-sample-based gradient. We then show in simulation how the variance of the gradient is reduced by three orders of magnitude, leading to better sample complexity compared to the standard policy gradient. On Atari, SoftTreeMax demonstrates up to 5x better performance in a faster run time compared to distributed PPO. Lastly, we demonstrate that high reward correlates with lower variance.

Improving Sample Efficiency in Evolutionary RL Using Off-Policy Ranking

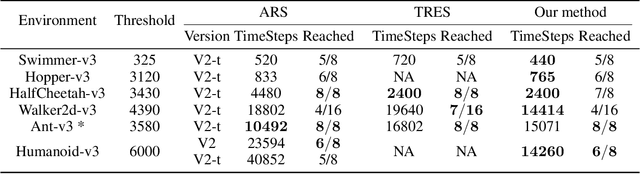
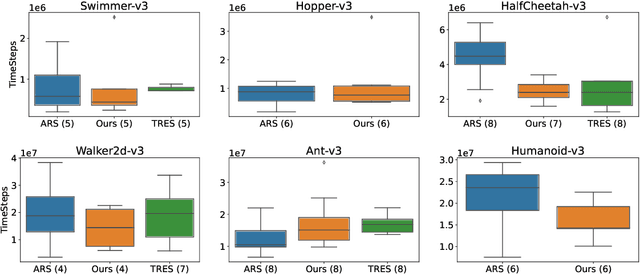
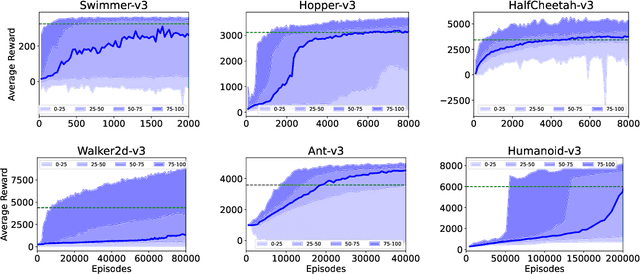
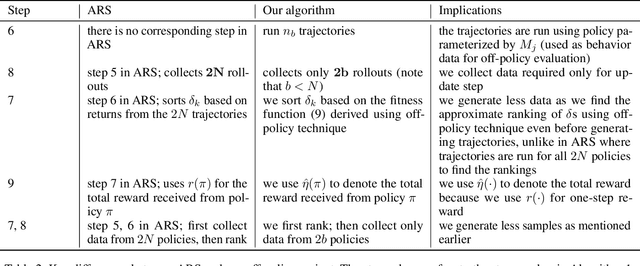
Evolution Strategy (ES) is a powerful black-box optimization technique based on the idea of natural evolution. In each of its iterations, a key step entails ranking candidate solutions based on some fitness score. For an ES method in Reinforcement Learning (RL), this ranking step requires evaluating multiple policies. This is presently done via on-policy approaches: each policy's score is estimated by interacting several times with the environment using that policy. This leads to a lot of wasteful interactions since, once the ranking is done, only the data associated with the top-ranked policies is used for subsequent learning. To improve sample efficiency, we propose a novel off-policy alternative for ranking, based on a local approximation for the fitness function. We demonstrate our idea in the context of a state-of-the-art ES method called the Augmented Random Search (ARS). Simulations in MuJoCo tasks show that, compared to the original ARS, our off-policy variant has similar running times for reaching reward thresholds but needs only around 70% as much data. It also outperforms the recent Trust Region ES. We believe our ideas should be extendable to other ES methods as well.

Approximate Q-learning and SARSA under the $ε$-greedy Policy: a Differential Inclusion Analysis

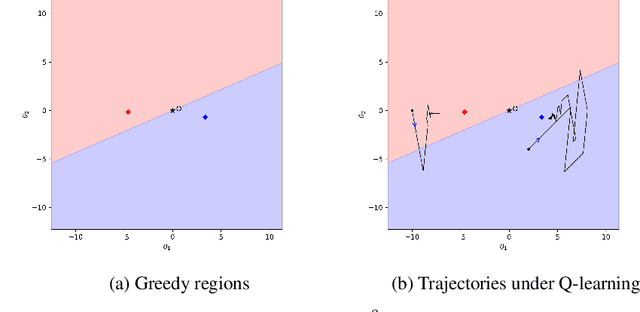
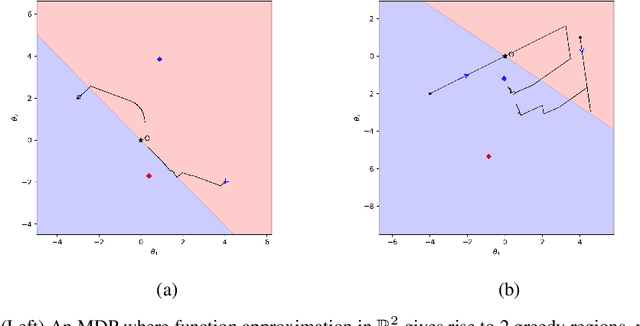
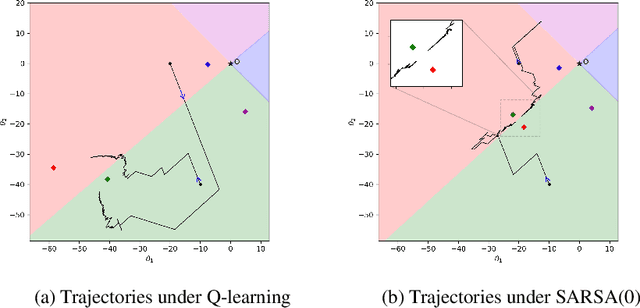
Q-learning and SARSA(0) with linear function approximation, under $\epsilon$-greedy exploration, are leading methods to estimate the optimal policy in Reinforcement Learning (RL). It has been empirically known that the discontinuous nature of the greedy policies causes these algorithms to exhibit complex phenomena such as i.) instability, ii.) policy oscillation and chattering, iii.) multiple attractors, and iv.) worst policy convergence. However, the literature lacks a formal recipe to explain these behaviors and this has been a long-standing open problem (Sutton, 1999). Our work addresses this by building the necessary mathematical framework using stochastic recursive inclusions and Differential Inclusions (DIs). From this novel viewpoint, our main result states that these approximate algorithms asymptotically converge to suitable invariant sets of DIs instead of differential equations, as is common elsewhere in RL. Furthermore, the nature of these deterministic DIs completely governs the limiting behaviors of these algorithms.

A Law of Iterated Logarithm for Multi-Agent Reinforcement Learning

In Multi-Agent Reinforcement Learning (MARL), multiple agents interact with a common environment, as also with each other, for solving a shared problem in sequential decision-making. It has wide-ranging applications in gaming, robotics, finance, etc. In this work, we derive a novel law of iterated logarithm for a family of distributed nonlinear stochastic approximation schemes that is useful in MARL. In particular, our result describes the convergence rate on almost every sample path where the algorithm converges. This result is the first of its kind in the distributed setup and provides deeper insights than the existing ones, which only discuss convergence rates in the expected or the CLT sense. Importantly, our result holds under significantly weaker assumptions: neither the gossip matrix needs to be doubly stochastic nor the stepsizes square summable. As an application, we show that, for the stepsize $n^{-\gamma}$ with $\gamma \in (0, 1),$ the distributed TD(0) algorithm with linear function approximation has a convergence rate of $O(\sqrt{n^{-\gamma} \ln n })$ a.s.; for the $1/n$ type stepsize, the same is $O(\sqrt{n^{-1} \ln \ln n})$ a.s. These decay rates do not depend on the graph depicting the interactions among the different agents.