Markov Chain Variance Estimation: A Stochastic Approximation Approach

We consider the problem of estimating the asymptotic variance of a function defined on a Markov chain, an important step for statistical inference of the stationary mean. We design the first recursive estimator that requires $O(1)$ computation at each step, does not require storing any historical samples or any prior knowledge of run-length, and has optimal $O(\frac{1}{n})$ rate of convergence for the mean-squared error (MSE) with provable finite sample guarantees. Here, $n$ refers to the total number of samples generated. The previously best-known rate of convergence in MSE was $O(\frac{\log n}{n})$, achieved by jackknifed estimators, which also do not enjoy these other desirable properties. Our estimator is based on linear stochastic approximation of an equivalent formulation of the asymptotic variance in terms of the solution of the Poisson equation. We generalize our estimator in several directions, including estimating the covariance matrix for vector-valued functions, estimating the stationary variance of a Markov chain, and approximately estimating the asymptotic variance in settings where the state space of the underlying Markov chain is large. We also show applications of our estimator in average reward reinforcement learning (RL), where we work with asymptotic variance as a risk measure to model safety-critical applications. We design a temporal-difference type algorithm tailored for policy evaluation in this context. We consider both the tabular and linear function approximation settings. Our work paves the way for developing actor-critic style algorithms for variance-constrained RL.

Optimal Top-Two Method for Best Arm Identification and Fluid Analysis

Top-$2$ methods have become popular in solving the best arm identification (BAI) problem. The best arm, or the arm with the largest mean amongst finitely many, is identified through an algorithm that at any sequential step independently pulls the empirical best arm, with a fixed probability $\beta$, and pulls the best challenger arm otherwise. The probability of incorrect selection is guaranteed to lie below a specified $\delta >0$. Information theoretic lower bounds on sample complexity are well known for BAI problem and are matched asymptotically as $\delta \rightarrow 0$ by computationally demanding plug-in methods. The above top 2 algorithm for any $\beta \in (0,1)$ has sample complexity within a constant of the lower bound. However, determining the optimal $\beta$ that matches the lower bound has proven difficult. In this paper, we address this and propose an optimal top-2 type algorithm. We consider a function of allocations anchored at a threshold. If it exceeds the threshold then the algorithm samples the empirical best arm. Otherwise, it samples the challenger arm. We show that the proposed algorithm is optimal as $\delta \rightarrow 0$. Our analysis relies on identifying a limiting fluid dynamics of allocations that satisfy a series of ordinary differential equations pasted together and that describe the asymptotic path followed by our algorithm. We rely on the implicit function theorem to show existence and uniqueness of these fluid ode's and to show that the proposed algorithm remains close to the ode solution.

CRIMED: Lower and Upper Bounds on Regret for Bandits with Unbounded Stochastic Corruption

We investigate the regret-minimisation problem in a multi-armed bandit setting with arbitrary corruptions. Similar to the classical setup, the agent receives rewards generated independently from the distribution of the arm chosen at each time. However, these rewards are not directly observed. Instead, with a fixed $\varepsilon\in (0,\frac{1}{2})$, the agent observes a sample from the chosen arm's distribution with probability $1-\varepsilon$, or from an arbitrary corruption distribution with probability $\varepsilon$. Importantly, we impose no assumptions on these corruption distributions, which can be unbounded. In this setting, accommodating potentially unbounded corruptions, we establish a problem-dependent lower bound on regret for a given family of arm distributions. We introduce CRIMED, an asymptotically-optimal algorithm that achieves the exact lower bound on regret for bandits with Gaussian distributions with known variance. Additionally, we provide a finite-sample analysis of CRIMED's regret performance. Notably, CRIMED can effectively handle corruptions with $\varepsilon$ values as high as $\frac{1}{2}$. Furthermore, we develop a tight concentration result for medians in the presence of arbitrary corruptions, even with $\varepsilon$ values up to $\frac{1}{2}$, which may be of independent interest. We also discuss an extension of the algorithm for handling misspecification in Gaussian model.

Optimal Best-Arm Identification in Bandits with Access to Offline Data

Learning paradigms based purely on offline data as well as those based solely on sequential online learning have been well-studied in the literature. In this paper, we consider combining offline data with online learning, an area less studied but of obvious practical importance. We consider the stochastic $K$-armed bandit problem, where our goal is to identify the arm with the highest mean in the presence of relevant offline data, with confidence $1-\delta$. We conduct a lower bound analysis on policies that provide such $1-\delta$ probabilistic correctness guarantees. We develop algorithms that match the lower bound on sample complexity when $\delta$ is small. Our algorithms are computationally efficient with an average per-sample acquisition cost of $\tilde{O}(K)$, and rely on a careful characterization of the optimality conditions of the lower bound problem.

Regret Minimization in Heavy-Tailed Bandits

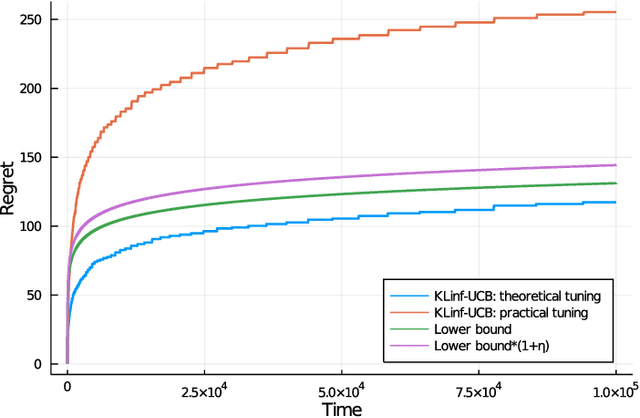
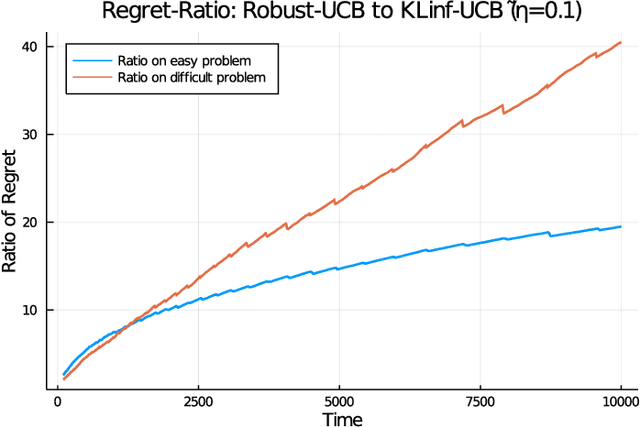
We revisit the classic regret-minimization problem in the stochastic multi-armed bandit setting when the arm-distributions are allowed to be heavy-tailed. Regret minimization has been well studied in simpler settings of either bounded support reward distributions or distributions that belong to a single parameter exponential family. We work under the much weaker assumption that the moments of order $(1+\epsilon)$ are uniformly bounded by a known constant B, for some given $\epsilon > 0$. We propose an optimal algorithm that matches the lower bound exactly in the first-order term. We also give a finite-time bound on its regret. We show that our index concentrates faster than the well known truncated or trimmed empirical mean estimators for the mean of heavy-tailed distributions. Computing our index can be computationally demanding. To address this, we develop a batch-based algorithm that is optimal up to a multiplicative constant depending on the batch size. We hence provide a controlled trade-off between statistical optimality and computational cost.

Optimal Best-Arm Identification Methods for Tail-Risk Measures

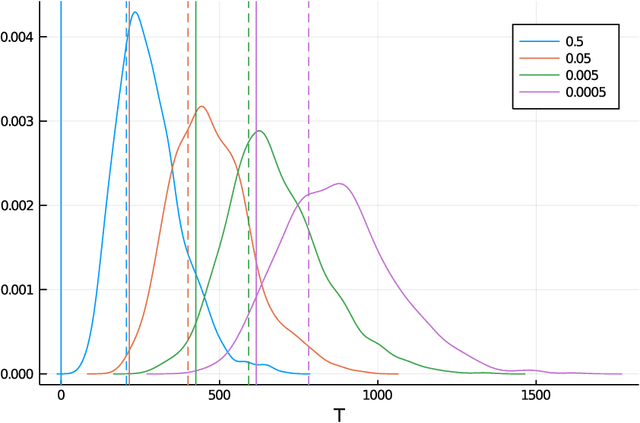
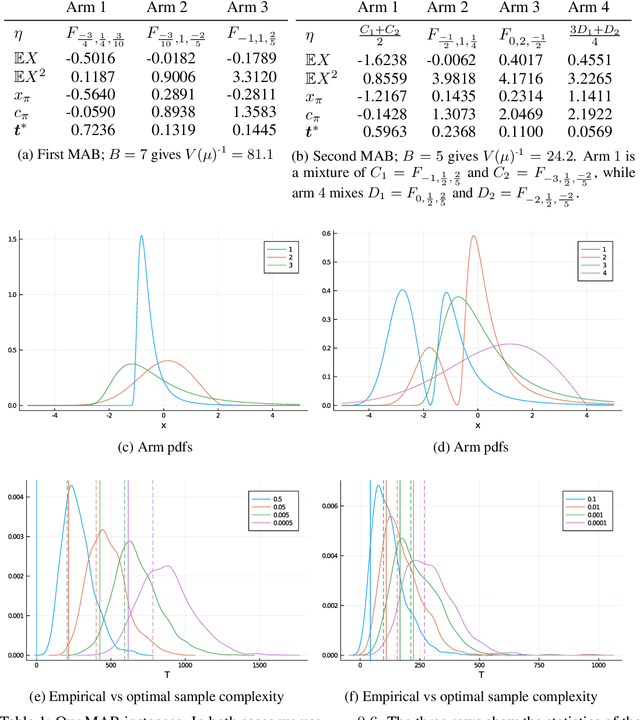
Conditional value-at-risk (CVaR) and value-at-risk (VaR) are popular tail-risk measures in finance and insurance industries where often the underlying probability distributions are heavy-tailed. We use the multi-armed bandit best-arm identification framework and consider the problem of identifying the arm-distribution from amongst finitely many that has the smallest CVaR or VaR. We first show that in the special case of arm-distributions belonging to a single-parameter exponential family, both these problems are equivalent to the best mean-arm identification problem, which is widely studied in the literature. This equivalence however is not true in general. We then propose optimal $\delta$-correct algorithms that act on general arm-distributions, including heavy-tailed distributions, that match the lower bound on the expected number of samples needed, asymptotically (as $ \delta$ approaches $0$). En-route, we also develop new non-asymptotic concentration inequalities for certain functions of these risk measures for the empirical distribution, that may have wider applicability.

Optimal best arm selection for general distributions

Given a finite set of unknown distributions $\textit{or arms}$ that can be sampled from, we consider the problem of identifying the one with the largest mean using a delta-correct algorithm (an adaptive, sequential algorithm that restricts the probability of error to a specified delta) that has minimum sample complexity. Lower bounds for delta-correct algorithms are well known. Further, delta-correct algorithms that match the lower bound asymptotically as delta reduces to zero have also been developed in literature when the arm distributions are restricted to a single parameter exponential family. In this paper, we first observe a negative result that some restrictions are essential as otherwise under a delta-correct algorithm, distributions with unbounded support would require an infinite number of samples in expectation. We then propose a delta-correct algorithm that matches the lower bound as delta reduces to zero under a mild restriction that a known bound on the expectation of a non-negative, increasing convex function (for example, the squared moment) of underlying random variables, exists. We also propose batch processing and identify optimal batch sizes to substantially speed up the proposed algorithm. This best arm selection problem is a well studied classic problem in the simulation community. It has many learning applications including in recommendation systems and in product selection.