Dipayan Sen
Adaptive Estimation of Random Vectors with Bandit Feedback
Apr 01, 2022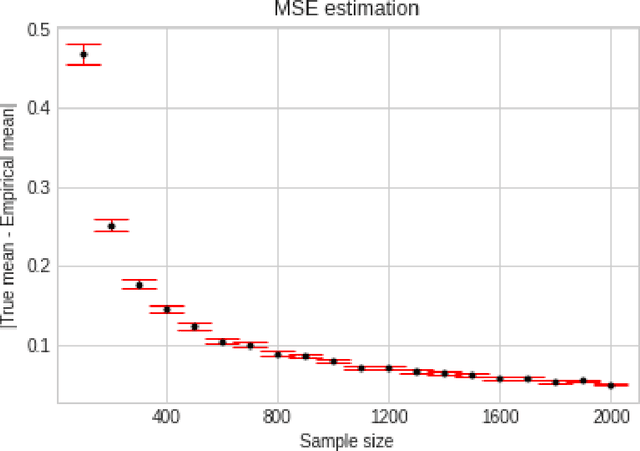
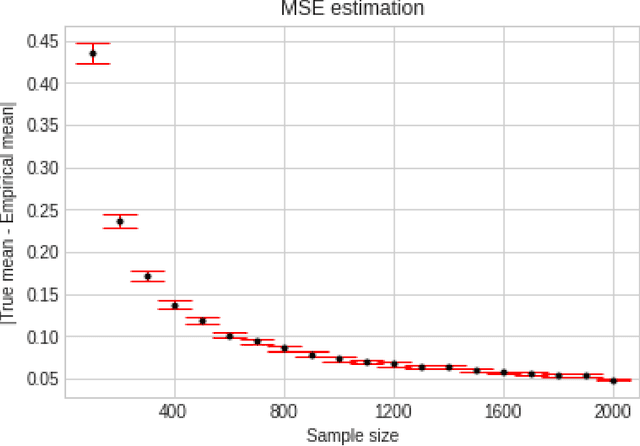
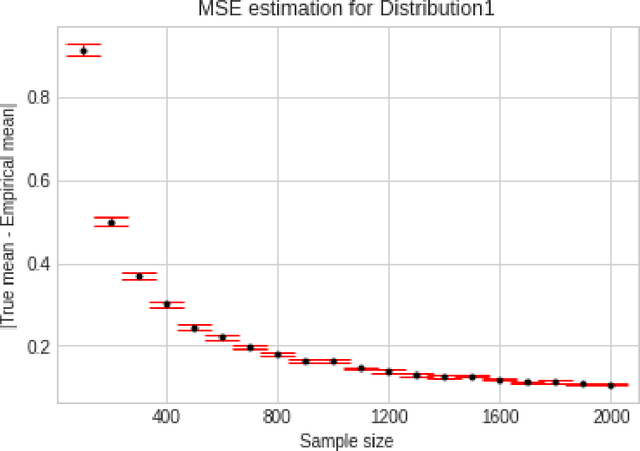
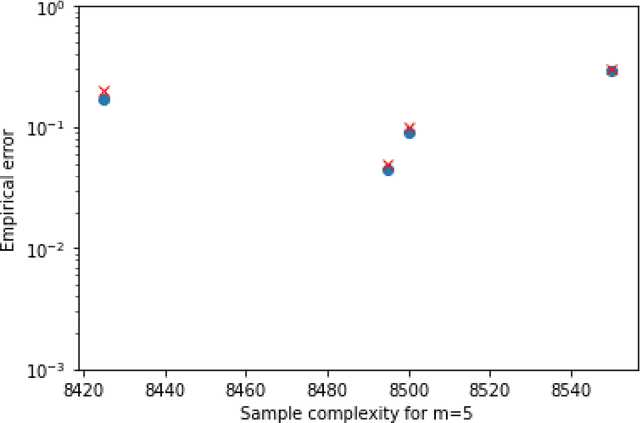
Abstract:We consider the problem of sequentially learning to estimate, in the mean squared error (MSE) sense, a Gaussian $K$-vector of unknown covariance by observing only $m < K$ of its entries in each round. This reduces to learning an optimal subset for estimating the entire vector. Towards this, we first establish an exponential concentration bound for an estimate of the MSE for each observable subset. We then frame the estimation problem with bandit feedback in the best-subset identification setting. We propose a variant of the successive elimination algorithm to cater to the adaptive estimation problem, and we derive an upper bound on the sample complexity of this algorithm. In addition, to understand the fundamental limit on the sample complexity of this adaptive estimation bandit problem, we derive a minimax lower bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge