Conditions on Preference Relations that Guarantee the Existence of Optimal Policies

Learning from Preferential Feedback (LfPF) plays an essential role in training Large Language Models, as well as certain types of interactive learning agents. However, a substantial gap exists between the theory and application of LfPF algorithms. Current results guaranteeing the existence of optimal policies in LfPF problems assume that both the preferences and transition dynamics are determined by a Markov Decision Process. We introduce the Direct Preference Process, a new framework for analyzing LfPF problems in partially-observable, non-Markovian environments. Within this framework, we establish conditions that guarantee the existence of optimal policies by considering the ordinal structure of the preferences. Using the von Neumann-Morgenstern Expected Utility Theorem, we show that the Direct Preference Process generalizes the standard reinforcement learning problem. Our findings narrow the gap between the empirical success and theoretical understanding of LfPF algorithms and provide future practitioners with the tools necessary for a more principled design of LfPF agents.

Policy Gradient Methods in the Presence of Symmetries and State Abstractions

Reinforcement learning on high-dimensional and complex problems relies on abstraction for improved efficiency and generalization. In this paper, we study abstraction in the continuous-control setting, and extend the definition of MDP homomorphisms to the setting of continuous state and action spaces. We derive a policy gradient theorem on the abstract MDP for both stochastic and deterministic policies. Our policy gradient results allow for leveraging approximate symmetries of the environment for policy optimization. Based on these theorems, we propose a family of actor-critic algorithms that are able to learn the policy and the MDP homomorphism map simultaneously, using the lax bisimulation metric. Finally, we introduce a series of environments with continuous symmetries to further demonstrate the ability of our algorithm for action abstraction in the presence of such symmetries. We demonstrate the effectiveness of our method on our environments, as well as on challenging visual control tasks from the DeepMind Control Suite. Our method's ability to utilize MDP homomorphisms for representation learning leads to improved performance, and the visualizations of the latent space clearly demonstrate the structure of the learned abstraction.

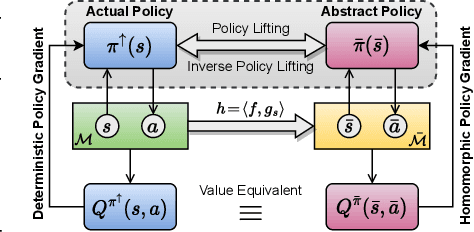
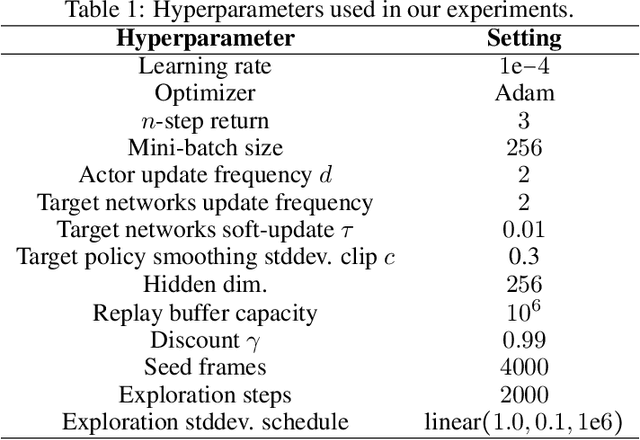
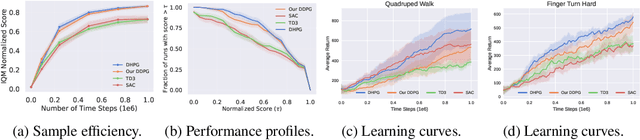
Continuous MDP Homomorphisms and Homomorphic Policy Gradient

Abstraction has been widely studied as a way to improve the efficiency and generalization of reinforcement learning algorithms. In this paper, we study abstraction in the continuous-control setting. We extend the definition of MDP homomorphisms to encompass continuous actions in continuous state spaces. We derive a policy gradient theorem on the abstract MDP, which allows us to leverage approximate symmetries of the environment for policy optimization. Based on this theorem, we propose an actor-critic algorithm that is able to learn the policy and the MDP homomorphism map simultaneously, using the lax bisimulation metric. We demonstrate the effectiveness of our method on benchmark tasks in the DeepMind Control Suite. Our method's ability to utilize MDP homomorphisms for representation learning leads to improved performance when learning from pixel observations.

Riemannian Diffusion Models

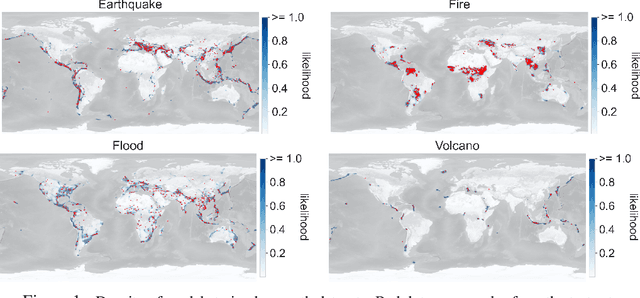
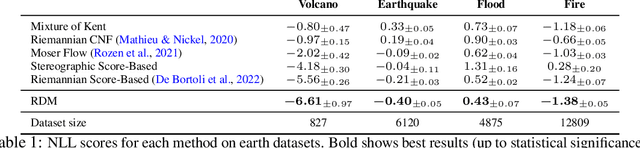
Diffusion models are recent state-of-the-art methods for image generation and likelihood estimation. In this work, we generalize continuous-time diffusion models to arbitrary Riemannian manifolds and derive a variational framework for likelihood estimation. Computationally, we propose new methods for computing the Riemannian divergence which is needed in the likelihood estimation. Moreover, in generalizing the Euclidean case, we prove that maximizing this variational lower-bound is equivalent to Riemannian score matching. Empirically, we demonstrate the expressive power of Riemannian diffusion models on a wide spectrum of smooth manifolds, such as spheres, tori, hyperboloids, and orthogonal groups. Our proposed method achieves new state-of-the-art likelihoods on all benchmarks.

Extracting Weighted Automata for Approximate Minimization in Language Modelling

In this paper we study the approximate minimization problem for language modelling. We assume we are given some language model as a black box. The objective is to obtain a weighted finite automaton (WFA) that fits within a given size constraint and which mimics the behaviour of the original model while minimizing some notion of distance between the black box and the extracted WFA. We provide an algorithm for the approximate minimization of black boxes trained for language modelling of sequential data over a one-letter alphabet. By reformulating the problem in terms of Hankel matrices, we leverage classical results on the approximation of Hankel operators, namely the celebrated Adamyan-Arov-Krein (AAK) theory. This allows us to use the spectral norm to measure the distance between the black box and the WFA. We provide theoretical guarantees to study the potentially infinite-rank Hankel matrix of the black box, without accessing the training data, and we prove that our method returns an asymptotically-optimal approximation.

MICo: Learning improved representations via sampling-based state similarity for Markov decision processes

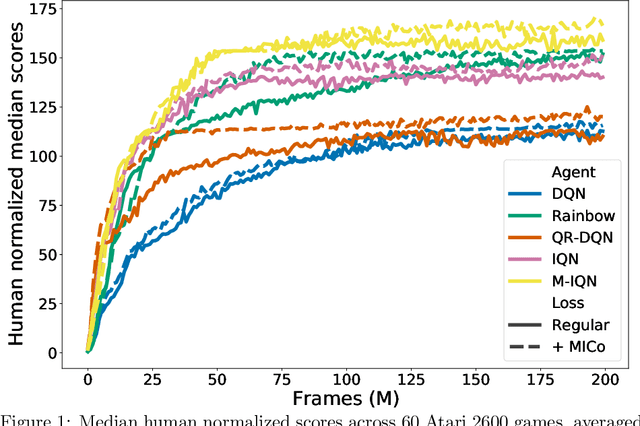
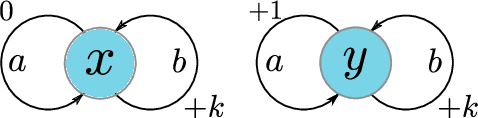
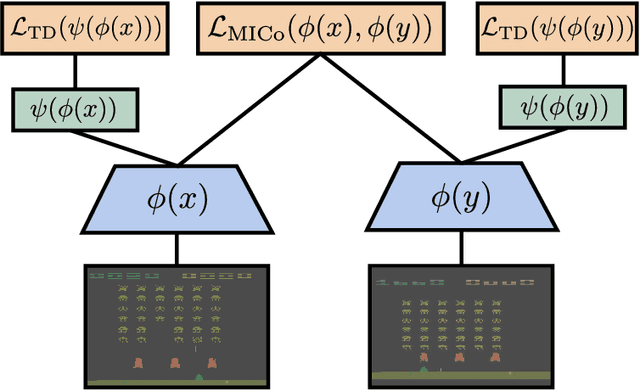
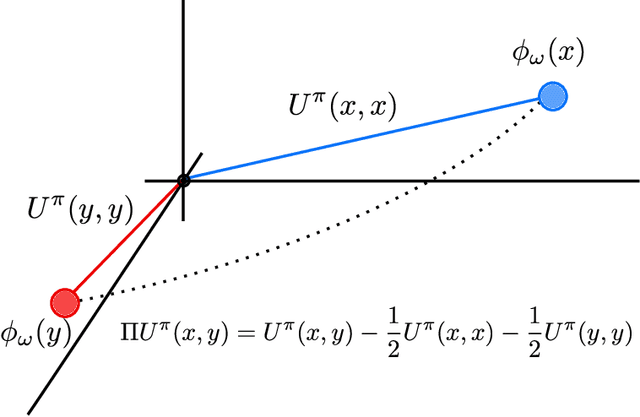
We present a new behavioural distance over the state space of a Markov decision process, and demonstrate the use of this distance as an effective means of shaping the learnt representations of deep reinforcement learning agents. While existing notions of state similarity are typically difficult to learn at scale due to high computational cost and lack of sample-based algorithms, our newly-proposed distance addresses both of these issues. In addition to providing detailed theoretical analysis, we provide empirical evidence that learning this distance alongside the value function yields structured and informative representations, including strong results on the Arcade Learning Environment benchmark.

A Study of Policy Gradient on a Class of Exactly Solvable Models

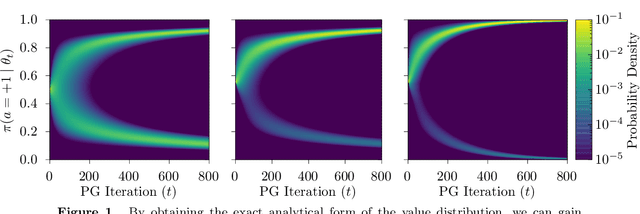
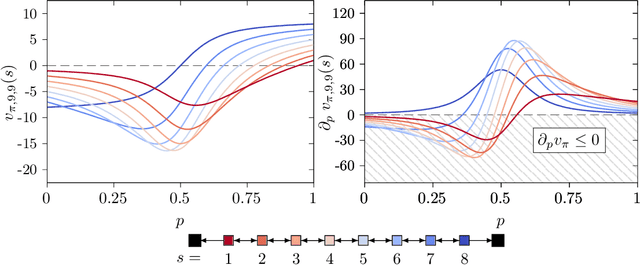
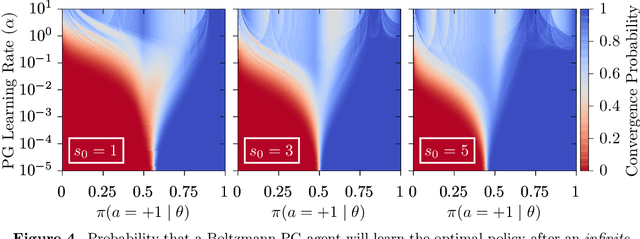
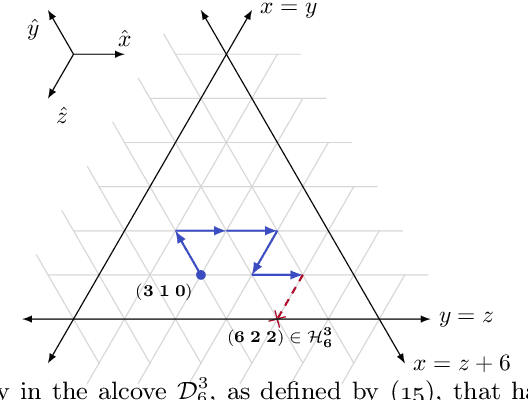
Policy gradient methods are extensively used in reinforcement learning as a way to optimize expected return. In this paper, we explore the evolution of the policy parameters, for a special class of exactly solvable POMDPs, as a continuous-state Markov chain, whose transition probabilities are determined by the gradient of the distribution of the policy's value. Our approach relies heavily on random walk theory, specifically on affine Weyl groups. We construct a class of novel partially observable environments with controllable exploration difficulty, in which the value distribution, and hence the policy parameter evolution, can be derived analytically. Using these environments, we analyze the probabilistic convergence of policy gradient to different local maxima of the value function. To our knowledge, this is the first approach developed to analytically compute the landscape of policy gradient in POMDPs for a class of such environments, leading to interesting insights into the difficulty of this problem.

A Distributional Analysis of Sampling-Based Reinforcement Learning Algorithms

We present a distributional approach to theoretical analyses of reinforcement learning algorithms for constant step-sizes. We demonstrate its effectiveness by presenting simple and unified proofs of convergence for a variety of commonly-used methods. We show that value-based methods such as TD($\lambda$) and $Q$-Learning have update rules which are contractive in the space of distributions of functions, thus establishing their exponentially fast convergence to a stationary distribution. We demonstrate that the stationary distribution obtained by any algorithm whose target is an expected Bellman update has a mean which is equal to the true value function. Furthermore, we establish that the distributions concentrate around their mean as the step-size shrinks. We further analyse the optimistic policy iteration algorithm, for which the contraction property does not hold, and formulate a probabilistic policy improvement property which entails the convergence of the algorithm.

Latent Variable Modelling with Hyperbolic Normalizing Flows

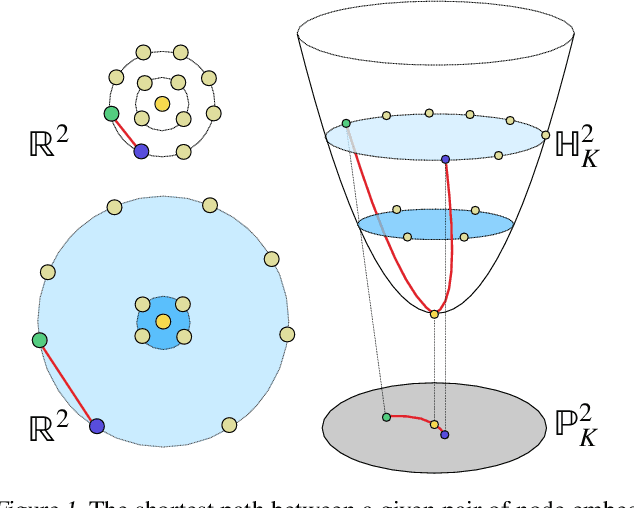
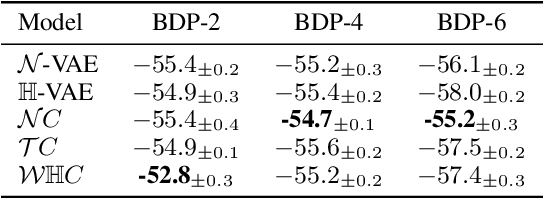
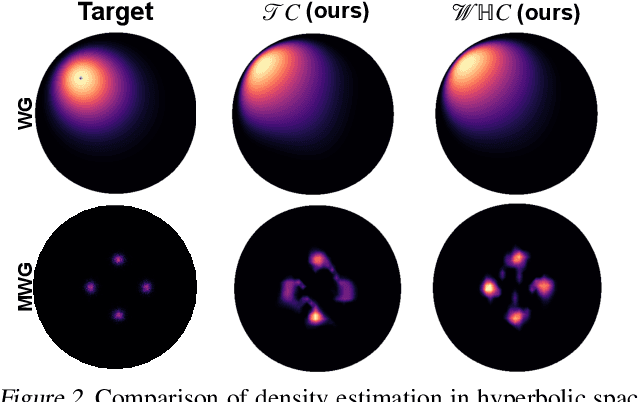
The choice of approximate posterior distributions plays a central role in stochastic variational inference (SVI). One effective solution is the use of normalizing flows \cut{defined on Euclidean spaces} to construct flexible posterior distributions. However, one key limitation of existing normalizing flows is that they are restricted to the Euclidean space and are ill-equipped to model data with an underlying hierarchical structure. To address this fundamental limitation, we present the first extension of normalizing flows to hyperbolic spaces. We first elevate normalizing flows to hyperbolic spaces using coupling transforms defined on the tangent bundle, termed Tangent Coupling ($\mathcal{TC}$). We further introduce Wrapped Hyperboloid Coupling ($\mathcal{W}\mathbb{H}C$), a fully invertible and learnable transformation that explicitly utilizes the geometric structure of hyperbolic spaces, allowing for expressive posteriors while being efficient to sample from. We demonstrate the efficacy of our novel normalizing flow over hyperbolic VAEs and Euclidean normalizing flows. Our approach achieves improved performance on density estimation, as well as reconstruction of real-world graph data, which exhibit a hierarchical structure. Finally, we show that our approach can be used to power a generative model over hierarchical data using hyperbolic latent variables.

Proceedings of the 11th workshop on Quantum Physics and Logic

This volume contains the proceedings of the 11th International Workshop on Quantum Physics and Logic (QPL 2014), which was held from the 4th to the 6th of June, 2014, at Kyoto University, Japan. The goal of the QPL workshop series is to bring together researchers working on mathematical foundations of quantum physics, quantum computing and spatio-temporal causal structures, and in particular those that use logical tools, ordered algebraic and category-theoretic structures, formal languages, semantic methods and other computer science methods for the study of physical behavior in general. Over the past few years, there has been growing activity in these foundational approaches, together with a renewed interest in the foundations of quantum theory, which complement the more mainstream research in quantum computation. Earlier workshops in this series, with the same acronym under the name "Quantum Programming Languages", were held in Ottawa (2003), Turku (2004), Chicago (2005), and Oxford (2006). The first QPL under the new name Quantum Physics and Logic was held in Reykjavik (2008), followed by Oxford (2009 and 2010), Nijmegen (2011), Brussels (2012) and Barcelona (2013).