Uncovering a Universal Abstract Algorithm for Modular Addition in Neural Networks

We propose a testable universality hypothesis, asserting that seemingly disparate neural network solutions observed in the simple task of modular addition are unified under a common abstract algorithm. While prior work interpreted variations in neuron-level representations as evidence for distinct algorithms, we demonstrate - through multi-level analyses spanning neurons, neuron clusters, and entire networks - that multilayer perceptrons and transformers universally implement the abstract algorithm we call the approximate Chinese Remainder Theorem. Crucially, we introduce approximate cosets and show that neurons activate exclusively on them. Furthermore, our theory works for deep neural networks (DNNs). It predicts that universally learned solutions in DNNs with trainable embeddings or more than one hidden layer require only O(log n) features, a result we empirically confirm. This work thus provides the first theory-backed interpretation of multilayer networks solving modular addition. It advances generalizable interpretability and opens a testable universality hypothesis for group multiplication beyond modular addition.

A Study of Policy Gradient on a Class of Exactly Solvable Models

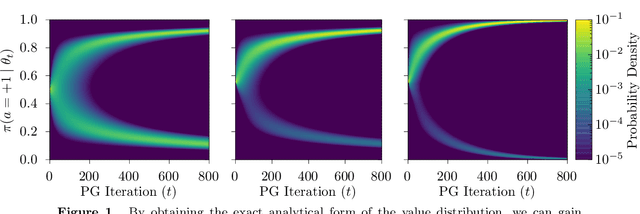
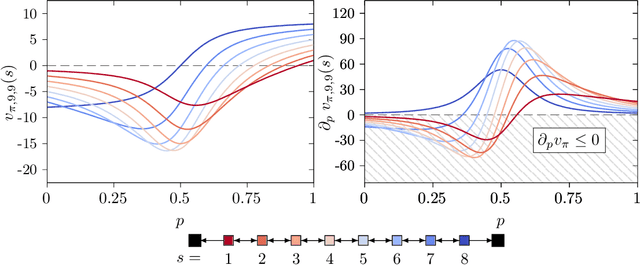
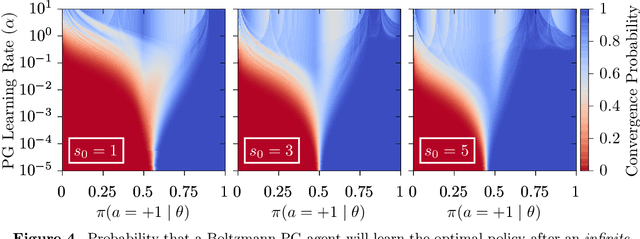
Policy gradient methods are extensively used in reinforcement learning as a way to optimize expected return. In this paper, we explore the evolution of the policy parameters, for a special class of exactly solvable POMDPs, as a continuous-state Markov chain, whose transition probabilities are determined by the gradient of the distribution of the policy's value. Our approach relies heavily on random walk theory, specifically on affine Weyl groups. We construct a class of novel partially observable environments with controllable exploration difficulty, in which the value distribution, and hence the policy parameter evolution, can be derived analytically. Using these environments, we analyze the probabilistic convergence of policy gradient to different local maxima of the value function. To our knowledge, this is the first approach developed to analytically compute the landscape of policy gradient in POMDPs for a class of such environments, leading to interesting insights into the difficulty of this problem.

oIRL: Robust Adversarial Inverse Reinforcement Learning with Temporally Extended Actions

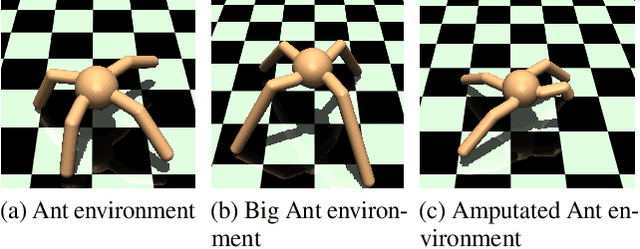
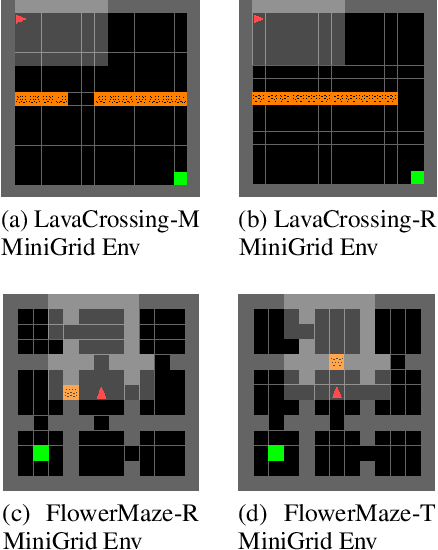
Explicit engineering of reward functions for given environments has been a major hindrance to reinforcement learning methods. While Inverse Reinforcement Learning (IRL) is a solution to recover reward functions from demonstrations only, these learned rewards are generally heavily \textit{entangled} with the dynamics of the environment and therefore not portable or \emph{robust} to changing environments. Modern adversarial methods have yielded some success in reducing reward entanglement in the IRL setting. In this work, we leverage one such method, Adversarial Inverse Reinforcement Learning (AIRL), to propose an algorithm that learns hierarchical disentangled rewards with a policy over options. We show that this method has the ability to learn \emph{generalizable} policies and reward functions in complex transfer learning tasks, while yielding results in continuous control benchmarks that are comparable to those of the state-of-the-art methods.