Pietro Vischia
Universal Scientific Education and Research Network, Italy, Universidad de Oviedo and ICTEA, Spain, MODE Collaboration
Strategic White Paper on AI Infrastructure for Particle, Nuclear, and Astroparticle Physics: Insights from JENA and EuCAIF
Mar 18, 2025



Abstract:Artificial intelligence (AI) is transforming scientific research, with deep learning methods playing a central role in data analysis, simulations, and signal detection across particle, nuclear, and astroparticle physics. Within the JENA communities-ECFA, NuPECC, and APPEC-and as part of the EuCAIF initiative, AI integration is advancing steadily. However, broader adoption remains constrained by challenges such as limited computational resources, a lack of expertise, and difficulties in transitioning from research and development (R&D) to production. This white paper provides a strategic roadmap, informed by a community survey, to address these barriers. It outlines critical infrastructure requirements, prioritizes training initiatives, and proposes funding strategies to scale AI capabilities across fundamental physics over the next five years.
Neuromorphic Readout for Hadron Calorimeters
Feb 18, 2025Abstract:We simulate hadrons impinging on a homogeneous lead-tungstate (PbWO4) calorimeter to investigate how the resulting light yield and its temporal structure, as detected by an array of light-sensitive sensors, can be processed by a neuromorphic computing system. Our model encodes temporal photon distributions as spike trains and employs a fully connected spiking neural network to estimate the total deposited energy, as well as the position and spatial distribution of the light emissions within the sensitive material. The extracted primitives offer valuable topological information about the shower development in the material, achieved without requiring a segmentation of the active medium. A potential nanophotonic implementation using III-V semiconductor nanowires is discussed. It can be both fast and energy efficient.
Large Physics Models: Towards a collaborative approach with Large Language Models and Foundation Models
Jan 09, 2025

Abstract:This paper explores ideas and provides a potential roadmap for the development and evaluation of physics-specific large-scale AI models, which we call Large Physics Models (LPMs). These models, based on foundation models such as Large Language Models (LLMs) - trained on broad data - are tailored to address the demands of physics research. LPMs can function independently or as part of an integrated framework. This framework can incorporate specialized tools, including symbolic reasoning modules for mathematical manipulations, frameworks to analyse specific experimental and simulated data, and mechanisms for synthesizing theories and scientific literature. We begin by examining whether the physics community should actively develop and refine dedicated models, rather than relying solely on commercial LLMs. We then outline how LPMs can be realized through interdisciplinary collaboration among experts in physics, computer science, and philosophy of science. To integrate these models effectively, we identify three key pillars: Development, Evaluation, and Philosophical Reflection. Development focuses on constructing models capable of processing physics texts, mathematical formulations, and diverse physical data. Evaluation assesses accuracy and reliability by testing and benchmarking. Finally, Philosophical Reflection encompasses the analysis of broader implications of LLMs in physics, including their potential to generate new scientific understanding and what novel collaboration dynamics might arise in research. Inspired by the organizational structure of experimental collaborations in particle physics, we propose a similarly interdisciplinary and collaborative approach to building and refining Large Physics Models. This roadmap provides specific objectives, defines pathways to achieve them, and identifies challenges that must be addressed to realise physics-specific large scale AI models.
TomOpt: Differential optimisation for task- and constraint-aware design of particle detectors in the context of muon tomography
Sep 25, 2023Abstract:We describe a software package, TomOpt, developed to optimise the geometrical layout and specifications of detectors designed for tomography by scattering of cosmic-ray muons. The software exploits differentiable programming for the modeling of muon interactions with detectors and scanned volumes, the inference of volume properties, and the optimisation cycle performing the loss minimisation. In doing so, we provide the first demonstration of end-to-end-differentiable and inference-aware optimisation of particle physics instruments. We study the performance of the software on a relevant benchmark scenarios and discuss its potential applications.
Applications and Techniques for Fast Machine Learning in Science
Oct 25, 2021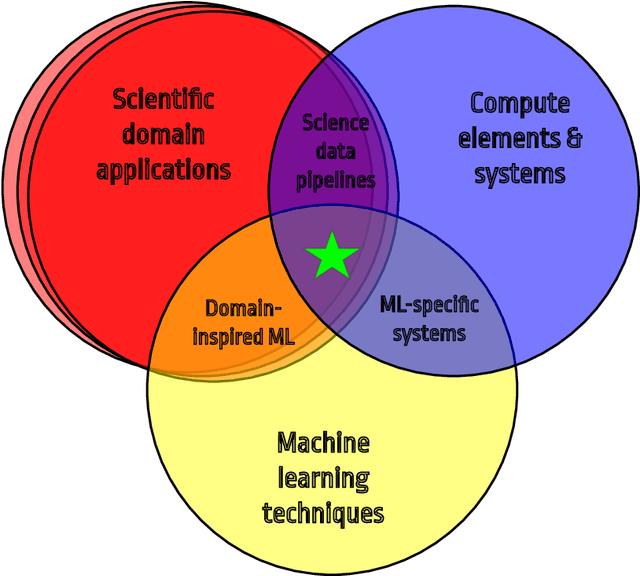
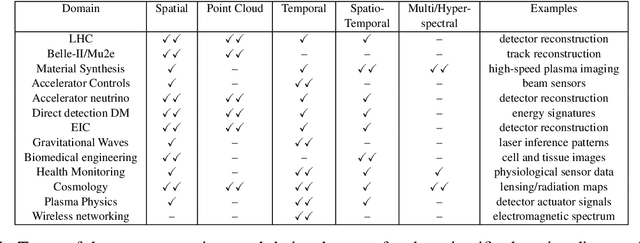
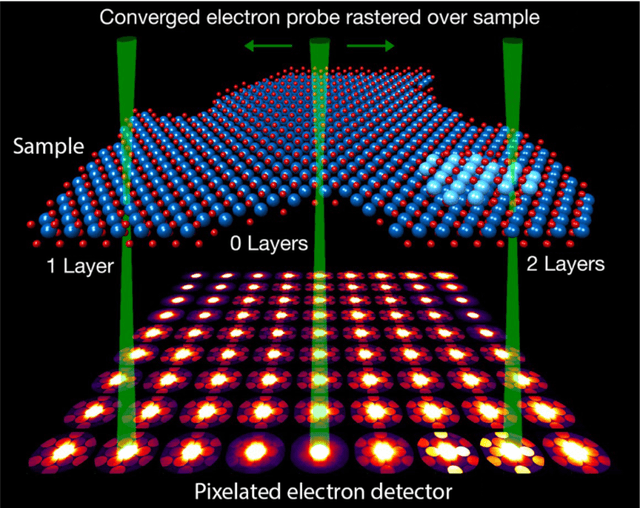
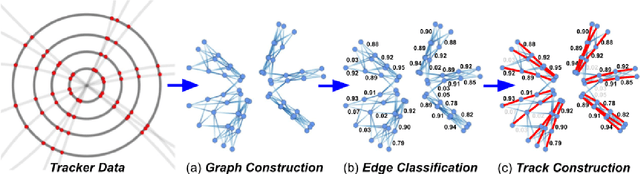
Abstract:In this community review report, we discuss applications and techniques for fast machine learning (ML) in science -- the concept of integrating power ML methods into the real-time experimental data processing loop to accelerate scientific discovery. The material for the report builds on two workshops held by the Fast ML for Science community and covers three main areas: applications for fast ML across a number of scientific domains; techniques for training and implementing performant and resource-efficient ML algorithms; and computing architectures, platforms, and technologies for deploying these algorithms. We also present overlapping challenges across the multiple scientific domains where common solutions can be found. This community report is intended to give plenty of examples and inspiration for scientific discovery through integrated and accelerated ML solutions. This is followed by a high-level overview and organization of technical advances, including an abundance of pointers to source material, which can enable these breakthroughs.
Advanced Multi-Variate Analysis Methods for New Physics Searches at the Large Hadron Collider
May 16, 2021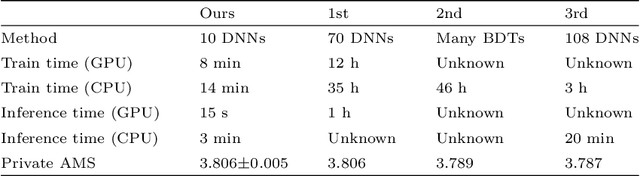
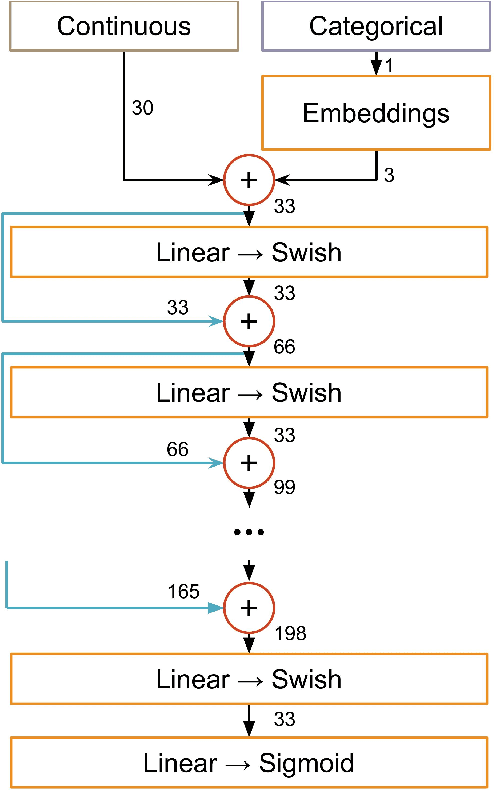
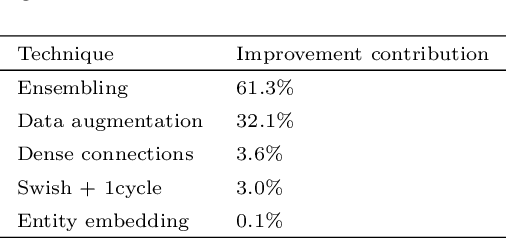
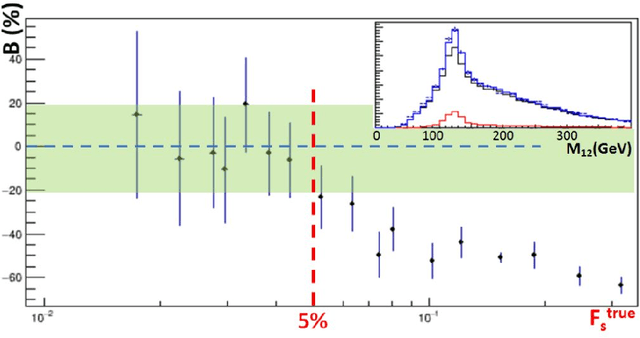
Abstract:Between the years 2015 and 2019, members of the Horizon 2020-funded Innovative Training Network named "AMVA4NewPhysics" studied the customization and application of advanced multivariate analysis methods and statistical learning tools to high-energy physics problems, as well as developed entirely new ones. Many of those methods were successfully used to improve the sensitivity of data analyses performed by the ATLAS and CMS experiments at the CERN Large Hadron Collider; several others, still in the testing phase, promise to further improve the precision of measurements of fundamental physics parameters and the reach of searches for new phenomena. In this paper, the most relevant new tools, among those studied and developed, are presented along with the evaluation of their performances.
Unfolding by Folding: a resampling approach to the problem of matrix inversion without actually inverting any matrix
Sep 07, 2020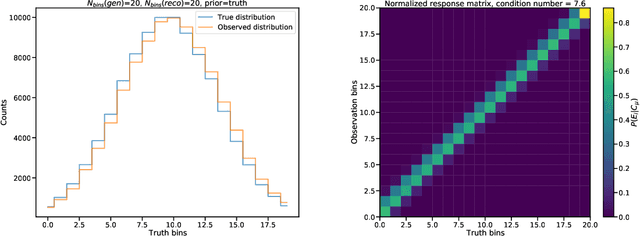

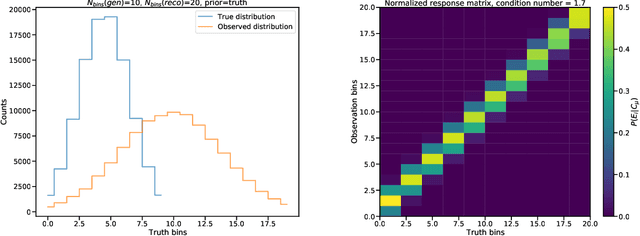
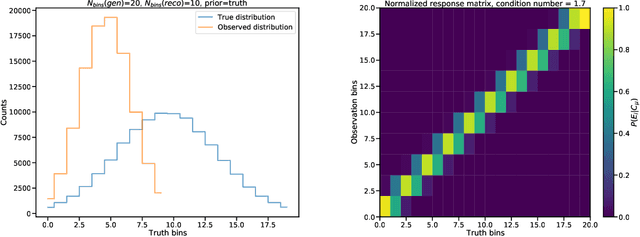
Abstract:Matrix inversion problems are often encountered in experimental physics, and in particular in high-energy particle physics, under the name of unfolding. The true spectrum of a physical quantity is deformed by the presence of a detector, resulting in an observed spectrum. If we discretize both the true and observed spectra into histograms, we can model the detector response via a matrix. Inferring a true spectrum starting from an observed spectrum requires therefore inverting the response matrix. Many methods exist in literature for this task, all starting from the observed spectrum and using a simulated true spectrum as a guide to obtain a meaningful solution in cases where the response matrix is not easily invertible. In this Manuscript, I take a different approach to the unfolding problem. Rather than inverting the response matrix and transforming the observed distribution into the most likely parent distribution in generator space, I sample many distributions in generator space, fold them through the original response matrix, and pick the generator-level distribution that yields the folded distribution closest to the data distribution. Regularization schemes can be introduced to treat the case where non-diagonal response matrices result in high-frequency oscillations of the solution in true space, and the introduced bias is studied. The algorithm performs as well as traditional unfolding algorithms in cases where the inverse problem is well-defined in terms of the discretization of the true and smeared space, and outperforms them in cases where the inverse problem is ill-defined---when the number of truth-space bins is larger than that of smeared-space bins. These advantages stem from the fact that the algorithm does not technically invert any matrix and uses only the data distribution as a guide to choose the best solution.
The Inverse Bagging Algorithm: Anomaly Detection by Inverse Bootstrap Aggregating
Nov 24, 2016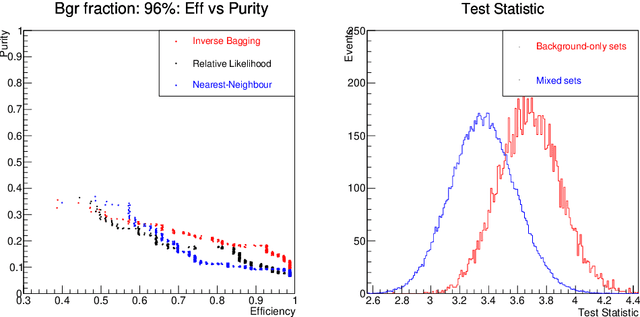
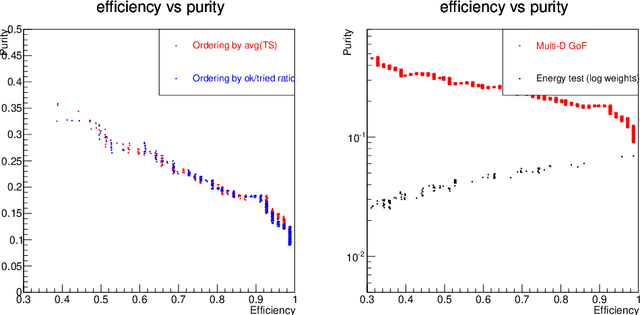
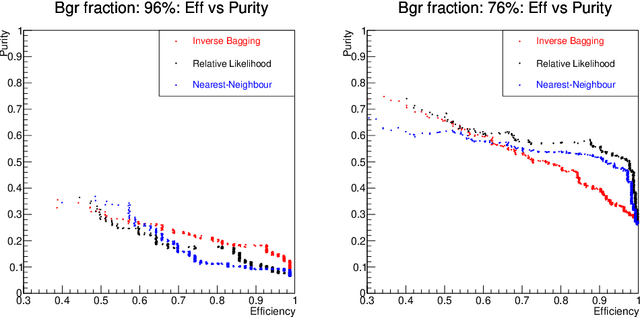
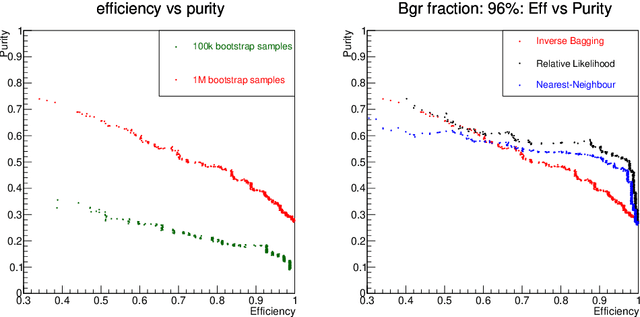
Abstract:For data sets populated by a very well modeled process and by another process of unknown probability density function (PDF), a desired feature when manipulating the fraction of the unknown process (either for enhancing it or suppressing it) consists in avoiding to modify the kinematic distributions of the well modeled one. A bootstrap technique is used to identify sub-samples rich in the well modeled process, and classify each event according to the frequency of it being part of such sub-samples. Comparisons with general MVA algorithms will be shown, as well as a study of the asymptotic properties of the method, making use of a public domain data set that models a typical search for new physics as performed at hadronic colliders such as the Large Hadron Collider (LHC).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge