Benchmarking 3D multi-coil NC-PDNet MRI reconstruction

Deep learning has shown great promise for MRI reconstruction from undersampled data, yet there is a lack of research on validating its performance in 3D parallel imaging acquisitions with non-Cartesian undersampling. In addition, the artifacts and the resulting image quality depend on the under-sampling pattern. To address this uncharted territory, we extend the Non-Cartesian Primal-Dual Network (NC-PDNet), a state-of-the-art unrolled neural network, to a 3D multi-coil setting. We evaluated the impact of channel-specific versus channel-agnostic training configurations and examined the effect of coil compression. Finally, we benchmark four distinct non-Cartesian undersampling patterns, with an acceleration factor of six, using the publicly available Calgary-Campinas dataset. Our results show that NC-PDNet trained on compressed data with varying input channel numbers achieves an average PSNR of 42.98 dB for 1 mm isotropic 32 channel whole-brain 3D reconstruction. With an inference time of 4.95sec and a GPU memory usage of 5.49 GB, our approach demonstrates significant potential for clinical research application.

Robust plug-and-play methods for highly accelerated non-Cartesian MRI reconstruction

Achieving high-quality Magnetic Resonance Imaging (MRI) reconstruction at accelerated acquisition rates remains challenging due to the inherent ill-posed nature of the inverse problem. Traditional Compressed Sensing (CS) methods, while robust across varying acquisition settings, struggle to maintain good reconstruction quality at high acceleration factors ($\ge$ 8). Recent advances in deep learning have improved reconstruction quality, but purely data-driven methods are prone to overfitting and hallucination effects, notably when the acquisition setting is varying. Plug-and-Play (PnP) approaches have been proposed to mitigate the pitfalls of both frameworks. In a nutshell, PnP algorithms amount to replacing suboptimal handcrafted CS priors with powerful denoising deep neural network (DNNs). However, in MRI reconstruction, existing PnP methods often yield suboptimal results due to instabilities in the proximal gradient descent (PGD) schemes and the lack of curated, noiseless datasets for training robust denoisers. In this work, we propose a fully unsupervised preprocessing pipeline to generate clean, noiseless complex MRI signals from multicoil data, enabling training of a high-performance denoising DNN. Furthermore, we introduce an annealed Half-Quadratic Splitting (HQS) algorithm to address the instability issues, leading to significant improvements over existing PnP algorithms. When combined with preconditioning techniques, our approach achieves state-of-the-art results, providing a robust and efficient solution for high-quality MRI reconstruction.

SNAKE-fMRI: A modular fMRI data simulator from the space-time domain to k-space and back

We propose a new, modular, open-source, Python-based 3D+time fMRI data simulation software, \emph{SNAKE-fMRI}, which stands for \emph{S}imulator from \emph{N}eurovascular coupling to \emph{A}cquisition of \emph{K}-space data for \emph{E}xploration of fMRI acquisition techniques.Unlike existing tools, the goal here is to simulate the complete chain of fMRI data acquisition, from the spatio-temporal design of evoked brain responses to various multi-coil k-space data 3D sampling strategies, with the possibility of extending the forward acquisition model to various noise and artifact sources while remaining memory-efficient.By using this \emph{in silico} setup, we are thus able to provide realistic and reproducible ground truth for fMRI reconstruction methods in 3D accelerated acquisition settings and explore the influence of critical parameters, such as the acceleration factor and signal-to-noise ratio~(SNR), on downstream tasks of image reconstruction and statistical analysis of evoked brain activity.We present three scenarios of increasing complexity to showcase the flexibility, versatility, and fidelity of \emph{SNAKE-fMRI}: From a temporally-fixed full 3D Cartesian to various 3D non-Cartesian sampling patterns, we can compare -- with reproducibility guarantees -- how experimental paradigms, acquisition strategies and reconstruction methods contribute and interact together, affecting the downstream statistical analysis.

Benchmarking learned non-Cartesian k-space trajectories and reconstruction networks

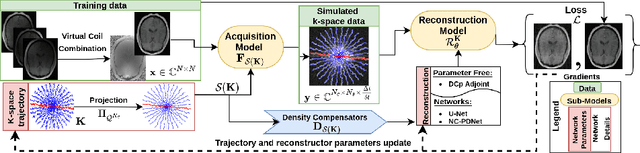
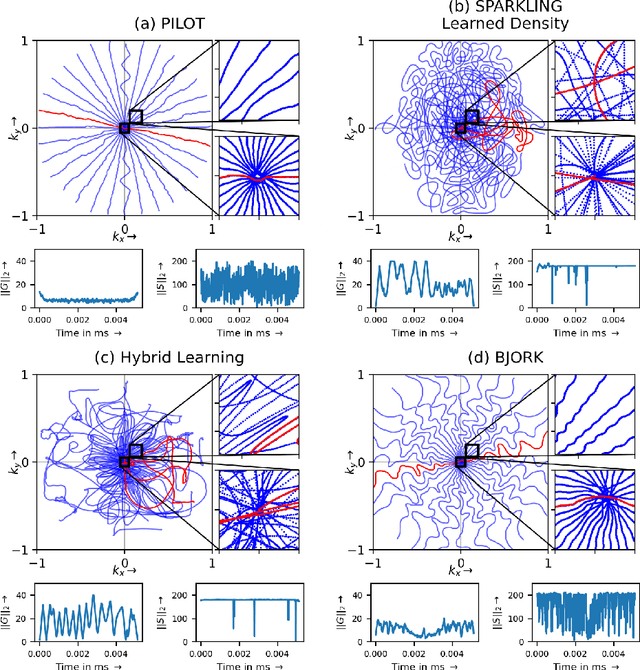
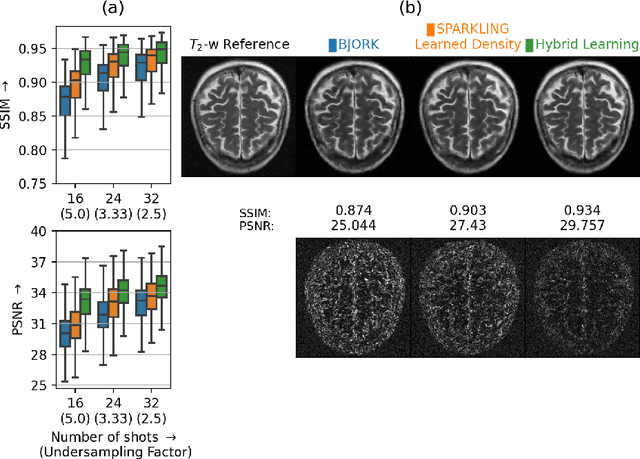
We benchmark the current existing methods to jointly learn non-Cartesian k-space trajectory and reconstruction: PILOT, BJORK, and compare them with those obtained from the recently developed generalized hybrid learning (HybLearn) framework. We present the advantages of using projected gradient descent to enforce MR scanner hardware constraints as compared to using added penalties in the cost function. Further, we use the novel HybLearn scheme to jointly learn and compare our results through a retrospective study on fastMRI validation dataset.

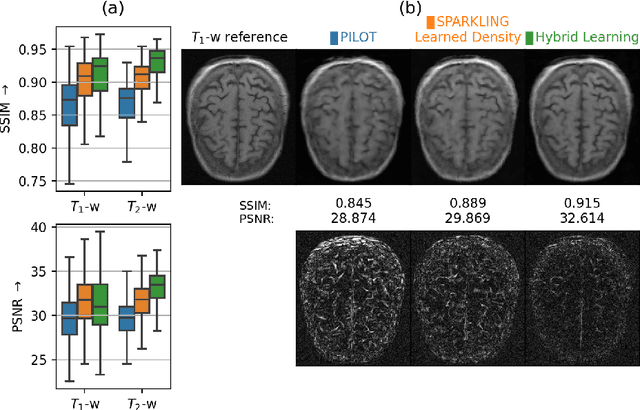
Hybrid learning of Non-Cartesian k-space trajectory and MR image reconstruction networks

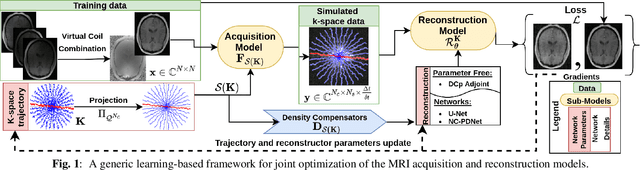
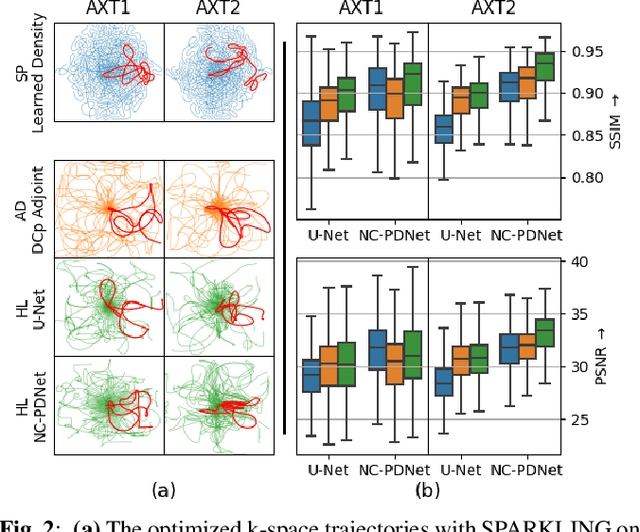
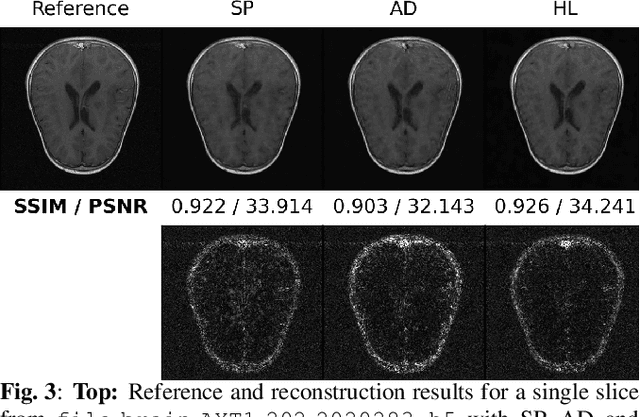
Compressed sensing (CS) in Magnetic resonance Imaging (MRI) essentially involves the optimization of 1) the sampling pattern in k-space under MR hardware constraints and 2) image reconstruction from the undersampled k-space data. Recently, deep learning methods have allowed the community to address both problems simultaneously, especially in the non-Cartesian acquisition setting. This paper aims to contribute to this field by tackling some major concerns in existing approaches.Regarding the learning of the sampling pattern, we perform ablation studies using parameter-free reconstructions like the density compensated (DCp) adjoint operator of the nonuniform fast Fourier transform (NUFFT) to ensure that the learned k-space trajectories actually sample the center of k-space densely. Additionally we optimize these trajectories by embedding a projected gradient descent algorithm over the hardware MR constraints. Later, we introduce a novel hybrid learning approach that operates across multiple resolutions to jointly optimize the reconstruction network and the k-space trajectory and present improved image reconstruction quality at 20-fold acceleration factor on T1 and T2-weighted images on the fastMRI dataset with SSIM scores of nearly 0.92-0.95 in our retrospective studies.

SHINE: SHaring the INverse Estimate from the forward pass for bi-level optimization and implicit models

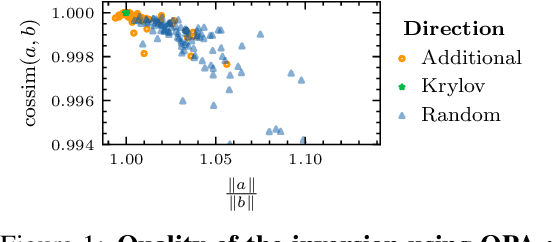
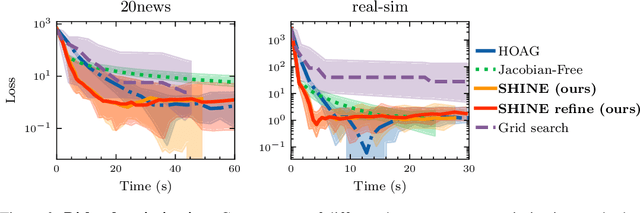
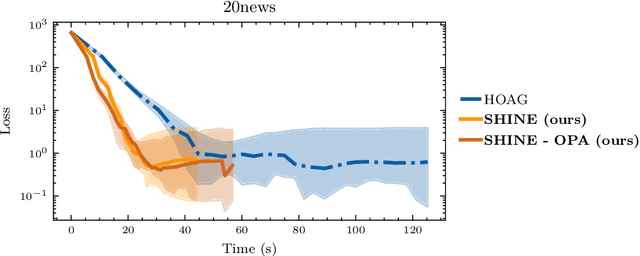
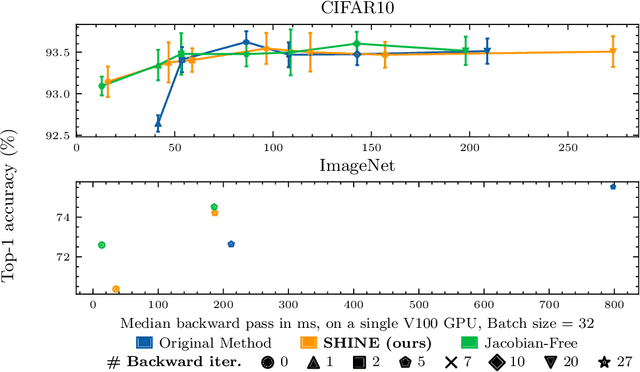
In recent years, implicit deep learning has emerged as a method to increase the depth of deep neural networks. While their training is memory-efficient, they are still significantly slower to train than their explicit counterparts. In Deep Equilibrium Models (DEQs), the training is performed as a bi-level problem, and its computational complexity is partially driven by the iterative inversion of a huge Jacobian matrix. In this paper, we propose a novel strategy to tackle this computational bottleneck from which many bi-level problems suffer. The main idea is to use the quasi-Newton matrices from the forward pass to efficiently approximate the inverse Jacobian matrix in the direction needed for the gradient computation. We provide a theorem that motivates using our method with the original forward algorithms. In addition, by modifying these forward algorithms, we further provide theoretical guarantees that our method asymptotically estimates the true implicit gradient. We empirically study this approach in many settings, ranging from hyperparameter optimization to large Multiscale DEQs applied to CIFAR and ImageNet. We show that it reduces the computational cost of the backward pass by up to two orders of magnitude. All this is achieved while retaining the excellent performance of the original models in hyperparameter optimization and on CIFAR, and giving encouraging and competitive results on ImageNet.

Is good old GRAPPA dead?

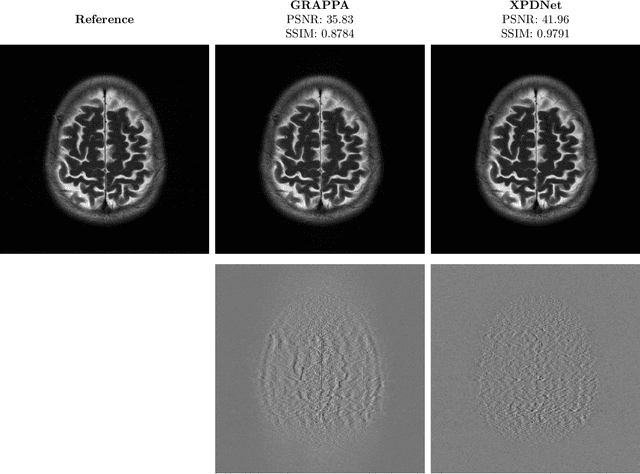
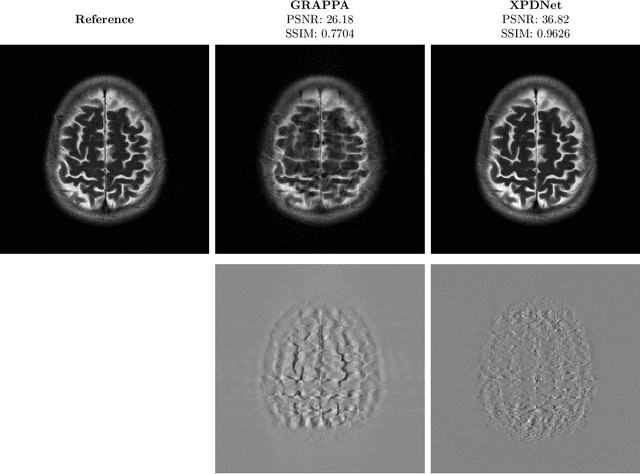
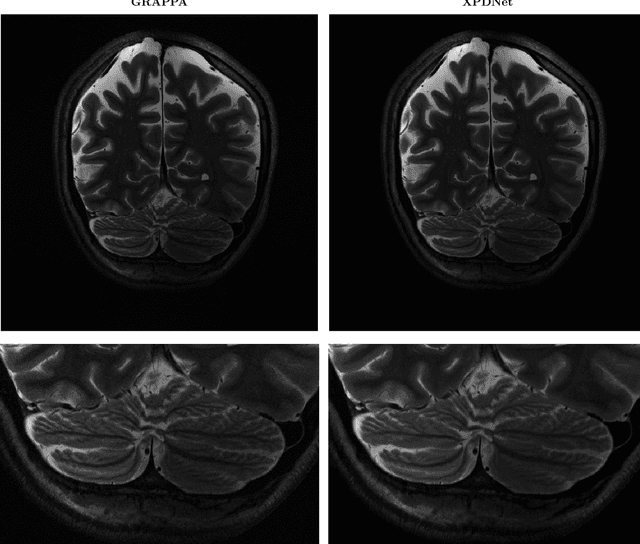
We perform a qualitative analysis of performance of XPDNet, a state-of-the-art deep learning approach for MRI reconstruction, compared to GRAPPA, a classical approach. We do this in multiple settings, in particular testing the robustness of the XPDNet to unseen settings, and show that the XPDNet can to some degree generalize well.

Learning the sampling density in 2D SPARKLING MRI acquisition for optimized image reconstruction

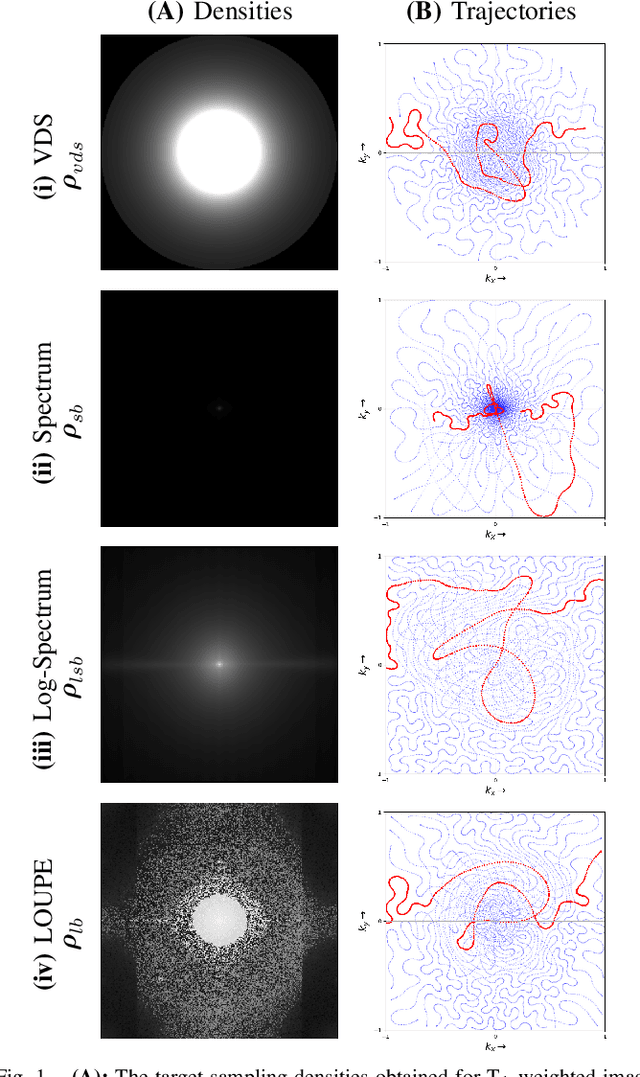
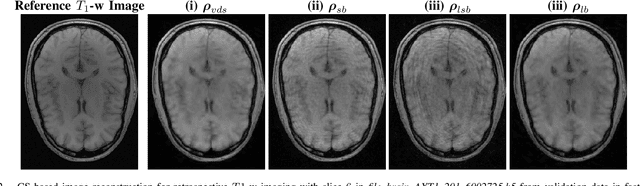
The SPARKLING algorithm was originally developed for accelerated 2D magnetic resonance imaging (MRI) in the compressed sensing (CS) context. It yields non-Cartesian sampling trajectories that jointly fulfill a target sampling density while each individual trajectory complies with MR hardware constraints. However, the two main limitations of SPARKLING are first that the optimal target sampling density is unknown and thus a user-defined parameter and second that this sampling pattern generation remains disconnected from MR image reconstruction thus from the optimization of image quality. Recently, datadriven learning schemes such as LOUPE have been proposed to learn a discrete sampling pattern, by jointly optimizing the whole pipeline from data acquisition to image reconstruction. In this work, we merge these methods with a state-of-the-art deep neural network for image reconstruction, called XPDNET, to learn the optimal target sampling density. Next, this density is used as input parameter to SPARKLING to obtain 20x accelerated non-Cartesian trajectories. These trajectories are tested on retrospective compressed sensing (CS) studies and show superior performance in terms of image quality with both deep learning (DL) and conventional CS reconstruction schemes.

Density Compensated Unrolled Networks for Non-Cartesian MRI Reconstruction

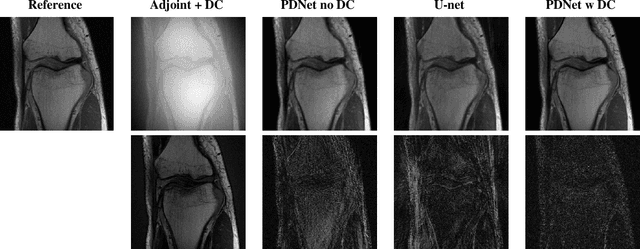
Deep neural networks have recently been thoroughly investigated as a powerful tool for MRI reconstruction. There is a lack of research, however, regarding their use for a specific setting of MRI, namely non-Cartesian acquisitions. In this work, we introduce a novel kind of deep neural networks to tackle this problem, namely density compensated unrolled neural networks, which rely on Density Compensation to correct the uneven weighting of the k-space. We assess their efficiency on the publicly available fastMRI dataset, and perform a small ablation study. Our results show that the density-compensated unrolled neural networks outperform the different baselines, and that all parts of the design are needed. We also open source our code, in particular a Non-Uniform Fast Fourier transform for TensorFlow.

State-of-the-Art Machine Learning MRI Reconstruction in 2020: Results of the Second fastMRI Challenge

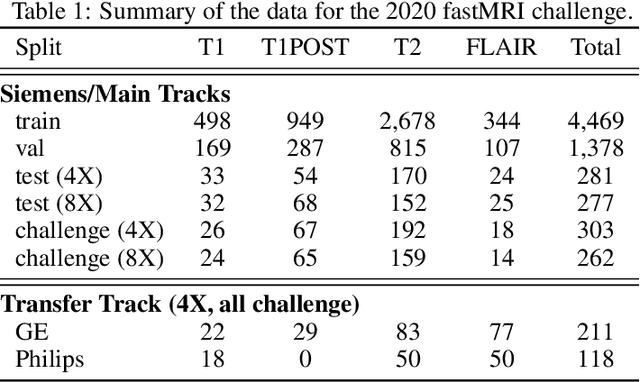
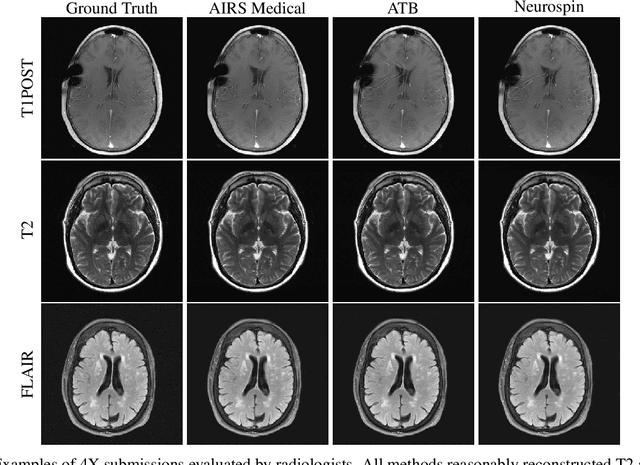
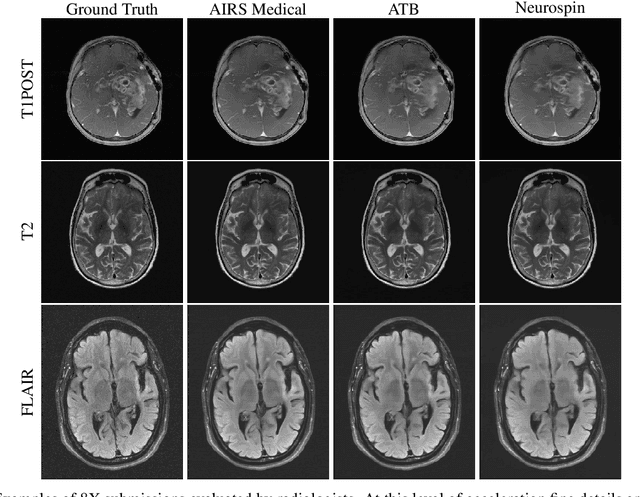
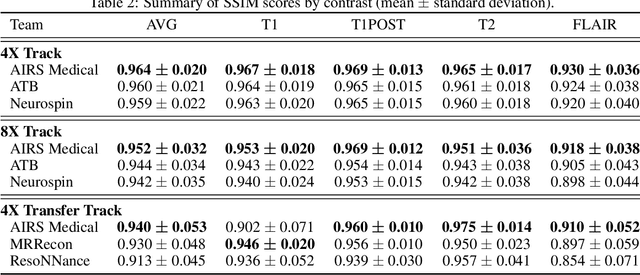
Accelerating MRI scans is one of the principal outstanding problems in the MRI research community. Towards this goal, we hosted the second fastMRI competition targeted towards reconstructing MR images with subsampled k-space data. We provided participants with data from 7,299 clinical brain scans (de-identified via a HIPAA-compliant procedure by NYU Langone Health), holding back the fully-sampled data from 894 of these scans for challenge evaluation purposes. In contrast to the 2019 challenge, we focused our radiologist evaluations on pathological assessment in brain images. We also debuted a new Transfer track that required participants to submit models evaluated on MRI scanners from outside the training set. We received 19 submissions from eight different groups. Results showed one team scoring best in both SSIM scores and qualitative radiologist evaluations. We also performed analysis on alternative metrics to mitigate the effects of background noise and collected feedback from the participants to inform future challenges. Lastly, we identify common failure modes across the submissions, highlighting areas of need for future research in the MRI reconstruction community.