Collaborative Learning with Shared Linear Representations: Statistical Rates and Optimal Algorithms

Collaborative learning enables multiple clients to learn shared feature representations across local data distributions, with the goal of improving model performance and reducing overall sample complexity. While empirical evidence shows the success of collaborative learning, a theoretical understanding of the optimal statistical rate remains lacking, even in linear settings. In this paper, we identify the optimal statistical rate when clients share a common low-dimensional linear representation. Specifically, we design a spectral estimator with local averaging that approximates the optimal solution to the least squares problem. We establish a minimax lower bound to demonstrate that our estimator achieves the optimal error rate. Notably, the optimal rate reveals two distinct phases. In typical cases, our rate matches the standard rate based on the parameter counting of the linear representation. However, a statistical penalty arises in collaborative learning when there are too many clients or when local datasets are relatively small. Furthermore, our results, unlike existing ones, show that, at a system level, collaboration always reduces overall sample complexity compared to independent client learning. In addition, at an individual level, we provide a more precise characterization of when collaboration benefits a client in transfer learning and private fine-tuning.

On the Convergence Rates of Federated Q-Learning across Heterogeneous Environments

Large-scale multi-agent systems are often deployed across wide geographic areas, where agents interact with heterogeneous environments. There is an emerging interest in understanding the role of heterogeneity in the performance of the federated versions of classic reinforcement learning algorithms. In this paper, we study synchronous federated Q-learning, which aims to learn an optimal Q-function by having $K$ agents average their local Q-estimates per $E$ iterations. We observe an interesting phenomenon on the convergence speeds in terms of $K$ and $E$. Similar to the homogeneous environment settings, there is a linear speed-up concerning $K$ in reducing the errors that arise from sampling randomness. Yet, in sharp contrast to the homogeneous settings, $E>1$ leads to significant performance degradation. Specifically, we provide a fine-grained characterization of the error evolution in the presence of environmental heterogeneity, which decay to zero as the number of iterations $T$ increases. The slow convergence of having $E>1$ turns out to be fundamental rather than an artifact of our analysis. We prove that, for a wide range of stepsizes, the $\ell_{\infty}$ norm of the error cannot decay faster than $\Theta (E/T)$. In addition, our experiments demonstrate that the convergence exhibits an interesting two-phase phenomenon. For any given stepsize, there is a sharp phase-transition of the convergence: the error decays rapidly in the beginning yet later bounces up and stabilizes. Provided that the phase-transition time can be estimated, choosing different stepsizes for the two phases leads to faster overall convergence.

Information-Theoretic Thresholds for the Alignments of Partially Correlated Graphs

This paper studies the problem of recovering the hidden vertex correspondence between two correlated random graphs. We propose the partially correlated Erd\H{o}s-R\'enyi graphs model, wherein a pair of induced subgraphs with a certain number are correlated. We investigate the information-theoretic thresholds for recovering the latent correlated subgraphs and the hidden vertex correspondence. We prove that there exists an optimal rate for partial recovery for the number of correlated nodes, above which one can correctly match a fraction of vertices and below which correctly matching any positive fraction is impossible, and we also derive an optimal rate for exact recovery. In the proof of possibility results, we propose correlated functional digraphs, which partition the edges of the intersection graph into two types of components, and bound the error probability by lower-order cumulant generating functions. The proof of impossibility results build upon the generalized Fano's inequality and the recovery thresholds settled in correlated Erd\H{o}s-R\'enyi graphs model.

On the best approximation by finite Gaussian mixtures

We consider the problem of approximating a general Gaussian location mixture by finite mixtures. The minimum order of finite mixtures that achieve a prescribed accuracy (measured by various $f$-divergences) is determined within constant factors for the family of mixing distributions with compactly support or appropriate assumptions on the tail probability including subgaussian and subexponential. While the upper bound is achieved using the technique of local moment matching, the lower bound is established by relating the best approximation error to the low-rank approximation of certain trigonometric moment matrices, followed by a refined spectral analysis of their minimum eigenvalue. In the case of Gaussian mixing distributions, this result corrects a previous lower bound in [Allerton Conference 48 (2010) 620-628].

Two Phases of Scaling Laws for Nearest Neighbor Classifiers

A scaling law refers to the observation that the test performance of a model improves as the number of training data increases. A fast scaling law implies that one can solve machine learning problems by simply boosting the data and the model sizes. Yet, in many cases, the benefit of adding more data can be negligible. In this work, we study the rate of scaling laws of nearest neighbor classifiers. We show that a scaling law can have two phases: in the first phase, the generalization error depends polynomially on the data dimension and decreases fast; whereas in the second phase, the error depends exponentially on the data dimension and decreases slowly. Our analysis highlights the complexity of the data distribution in determining the generalization error. When the data distributes benignly, our result suggests that nearest neighbor classifier can achieve a generalization error that depends polynomially, instead of exponentially, on the data dimension.

Federated Learning in the Presence of Adversarial Client Unavailability

Federated learning is a decentralized machine learning framework wherein not all clients are able to participate in each round. An emerging line of research is devoted to tackling arbitrary client unavailability. Existing theoretical analysis imposes restrictive structural assumptions on the unavailability patterns, and their proposed algorithms were tailored to those assumptions. In this paper, we relax those assumptions and consider adversarial client unavailability. To quantify the degrees of client unavailability, we use the notion of {\em $\epsilon$-adversary dropout fraction}. For both non-convex and strongly-convex global objectives, we show that simple variants of FedAvg or FedProx, albeit completely agnostic to $\epsilon$, converge to an estimation error on the order of $\epsilon (G^2 + \sigma^2)$, where $G$ is a heterogeneity parameter and $\sigma^2$ is the noise level. We prove that this estimation error is minimax-optimal. We also show that the variants of FedAvg or FedProx have convergence speeds $O(1/\sqrt{T})$ for non-convex objectives and $O(1/T)$ for strongly-convex objectives, both of which are the best possible for any first-order method that only has access to noisy gradients. Our proofs build upon a tight analysis of the selection bias that persists in the entire learning process. We validate our theoretical prediction through numerical experiments on synthetic and real-world datasets.

Global Convergence of Federated Learning for Mixed Regression

This paper studies the problem of model training under Federated Learning when clients exhibit cluster structure. We contextualize this problem in mixed regression, where each client has limited local data generated from one of $k$ unknown regression models. We design an algorithm that achieves global convergence from any initialization, and works even when local data volume is highly unbalanced -- there could exist clients that contain $O(1)$ data points only. Our algorithm first runs moment descent on a few anchor clients (each with $\tilde{\Omega}(k)$ data points) to obtain coarse model estimates. Then each client alternately estimates its cluster labels and refines the model estimates based on FedAvg or FedProx. A key innovation in our analysis is a uniform estimate on the clustering errors, which we prove by bounding the VC dimension of general polynomial concept classes based on the theory of algebraic geometry.

Deep Active Learning with Noise Stability

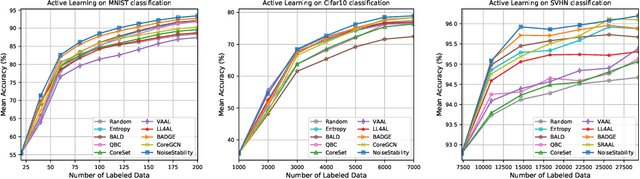
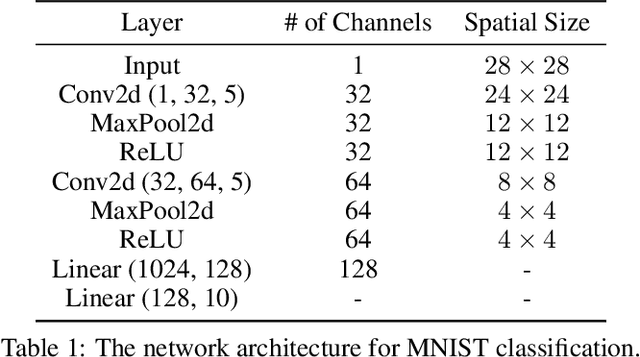
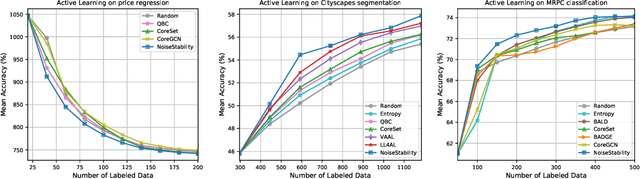
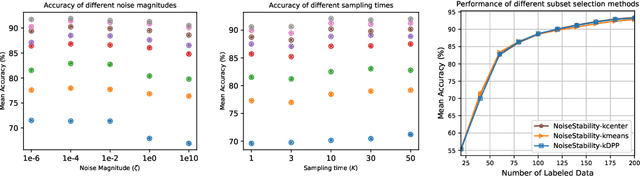
Uncertainty estimation for unlabeled data is crucial to active learning. With a deep neural network employed as the backbone model, the data selection process is highly challenging due to the potential over-confidence of the model inference. Existing methods resort to special learning fashions (e.g. adversarial) or auxiliary models to address this challenge. This tends to result in complex and inefficient pipelines, which would render the methods impractical. In this work, we propose a novel algorithm that leverages noise stability to estimate data uncertainty in a Single-Training Multi-Inference fashion. The key idea is to measure the output derivation from the original observation when the model parameters are randomly perturbed by noise. We provide theoretical analyses by leveraging the small Gaussian noise theory and demonstrate that our method favors a subset with large and diverse gradients. Despite its simplicity, our method outperforms the state-of-the-art active learning baselines in various tasks, including computer vision, natural language processing, and structural data analysis.

Boosting Active Learning via Improving Test Performance

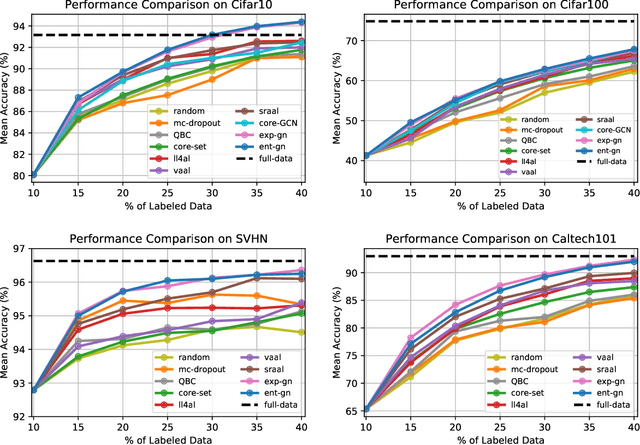
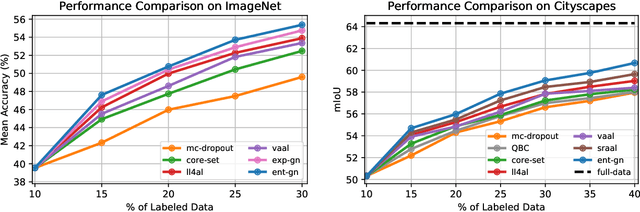
Central to active learning (AL) is what data should be selected for annotation. Existing works attempt to select highly uncertain or informative data for annotation. Nevertheless, it remains unclear how selected data impacts the test performance of the task model used in AL. In this work, we explore such an impact by theoretically proving that selecting unlabeled data of higher gradient norm leads to a lower upper bound of test loss, resulting in a better test performance. However, due to the lack of label information, directly computing gradient norm for unlabeled data is infeasible. To address this challenge, we propose two schemes, namely expected-gradnorm and entropy-gradnorm. The former computes the gradient norm by constructing an expected empirical loss while the latter constructs an unsupervised loss with entropy. Furthermore, we integrate the two schemes in a universal AL framework. We evaluate our method on classical image classification and semantic segmentation tasks. To demonstrate its competency in domain applications and its robustness to noise, we also validate our method on a cellular imaging analysis task, namely cryo-Electron Tomography subtomogram classification. Results demonstrate that our method achieves superior performance against the state-of-the-art. Our source code is available at https://github.com/xulabs/aitom

Achieving Statistical Optimality of Federated Learning: Beyond Stationary Points

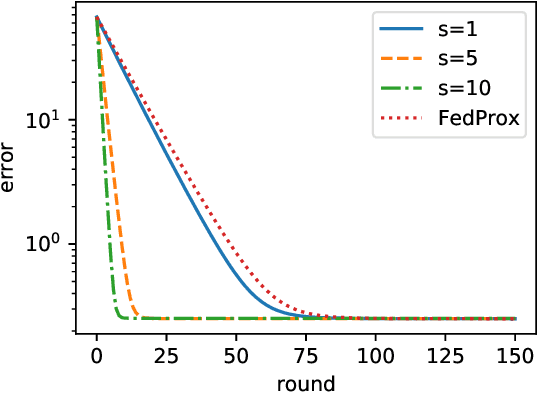
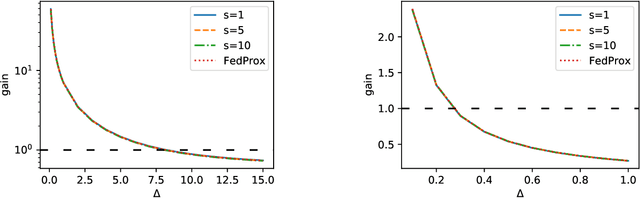
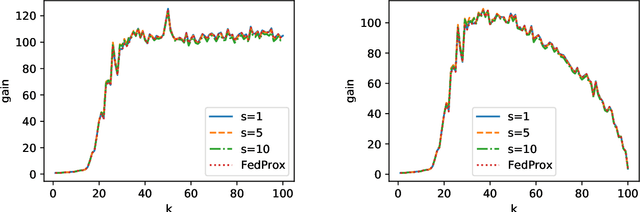
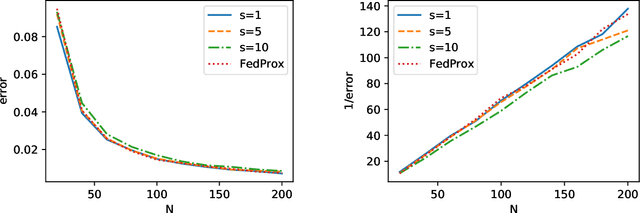
Federated Learning (FL) is a promising framework that has great potentials in privacy preservation and in lowering the computation load at the cloud. FedAvg and FedProx are two widely adopted algorithms. However, recent work raised concerns on these two methods: (1) their fixed points do not correspond to the stationary points of the original optimization problem, and (2) the common model found might not generalize well locally. In this paper, we alleviate these concerns. Towards this, we adopt the statistical learning perspective yet allow the distributions to be heterogeneous and the local data to be unbalanced. We show, in the general kernel regression setting, that both FedAvg and FedProx converge to the minimax-optimal error rates. Moreover, when the kernel function has a finite rank, the convergence is exponentially fast. Our results further analytically quantify the impact of the model heterogeneity and characterize the federation gain - the reduction of the estimation error for a worker to join the federated learning compared to the best local estimator. To the best of our knowledge, we are the first to show the achievability of minimax error rates under FedAvg and FedProx, and the first to characterize the gains in joining FL. Numerical experiments further corroborate our theoretical findings on the statistical optimality of FedAvg and FedProx and the federation gains.