Exponential Moving Average of Weights in Deep Learning: Dynamics and Benefits

Weight averaging of Stochastic Gradient Descent (SGD) iterates is a popular method for training deep learning models. While it is often used as part of complex training pipelines to improve generalization or serve as a `teacher' model, weight averaging lacks proper evaluation on its own. In this work, we present a systematic study of the Exponential Moving Average (EMA) of weights. We first explore the training dynamics of EMA, give guidelines for hyperparameter tuning, and highlight its good early performance, partly explaining its success as a teacher. We also observe that EMA requires less learning rate decay compared to SGD since averaging naturally reduces noise, introducing a form of implicit regularization. Through extensive experiments, we show that EMA solutions differ from last-iterate solutions. EMA models not only generalize better but also exhibit improved i) robustness to noisy labels, ii) prediction consistency, iii) calibration and iv) transfer learning. Therefore, we suggest that an EMA of weights is a simple yet effective plug-in to improve the performance of deep learning models.

Achieving Optimal Breakdown for Byzantine Robust Gossip

Distributed approaches have many computational benefits, but they are vulnerable to attacks from a subset of devices transmitting incorrect information. This paper investigates Byzantine-resilient algorithms in a decentralized setting, where devices communicate directly with one another. We investigate the notion of breakdown point, and show an upper bound on the number of adversaries that decentralized algorithms can tolerate. We introduce $\mathrm{CG}^+$, an algorithm at the intersection of $\mathrm{ClippedGossip}$ and $\mathrm{NNA}$, two popular approaches for robust decentralized learning. $\mathrm{CG}^+$ meets our upper bound, and thus obtains optimal robustness guarantees, whereas neither of the existing two does. We provide experimental evidence for this gap by presenting an attack tailored to sparse graphs which breaks $\mathrm{NNA}$ but against which $\mathrm{CG}^+$ is robust.

Byzantine-Robust Gossip: Insights from a Dual Approach

Distributed approaches have many computational benefits, but they are vulnerable to attacks from a subset of devices transmitting incorrect information. This paper investigates Byzantine-resilient algorithms in a decentralized setting, where devices communicate directly with one another. We leverage the so-called dual approach to design a general robust decentralized optimization method. We provide both global and local clipping rules in the special case of average consensus, with tight convergence guarantees. These clipping rules are practical, and yield results that finely characterize the impact of Byzantine nodes, highlighting for instance a qualitative difference in convergence between global and local clipping thresholds. Lastly, we demonstrate that they can serve as a basis for designing efficient attacks.

The Relative Gaussian Mechanism and its Application to Private Gradient Descent

The Gaussian Mechanism (GM), which consists in adding Gaussian noise to a vector-valued query before releasing it, is a standard privacy protection mechanism. In particular, given that the query respects some L2 sensitivity property (the L2 distance between outputs on any two neighboring inputs is bounded), GM guarantees R\'enyi Differential Privacy (RDP). Unfortunately, precisely bounding the L2 sensitivity can be hard, thus leading to loose privacy bounds. In this work, we consider a Relative L2 sensitivity assumption, in which the bound on the distance between two query outputs may also depend on their norm. Leveraging this assumption, we introduce the Relative Gaussian Mechanism (RGM), in which the variance of the noise depends on the norm of the output. We prove tight bounds on the RDP parameters under relative L2 sensitivity, and characterize the privacy loss incurred by using output-dependent noise. In particular, we show that RGM naturally adapts to a latent variable that would control the norm of the output. Finally, we instantiate our framework to show tight guarantees for Private Gradient Descent, a problem that naturally fits our relative L2 sensitivity assumption.

Revisiting Gradient Clipping: Stochastic bias and tight convergence guarantees

Gradient clipping is a popular modification to standard (stochastic) gradient descent, at every iteration limiting the gradient norm to a certain value $c >0$. It is widely used for example for stabilizing the training of deep learning models (Goodfellow et al., 2016), or for enforcing differential privacy (Abadi et al., 2016). Despite popularity and simplicity of the clipping mechanism, its convergence guarantees often require specific values of $c$ and strong noise assumptions. In this paper, we give convergence guarantees that show precise dependence on arbitrary clipping thresholds $c$ and show that our guarantees are tight with both deterministic and stochastic gradients. In particular, we show that (i) for deterministic gradient descent, the clipping threshold only affects the higher-order terms of convergence, (ii) in the stochastic setting convergence to the true optimum cannot be guaranteed under the standard noise assumption, even under arbitrary small step-sizes. We give matching upper and lower bounds for convergence of the gradient norm when running clipped SGD, and illustrate these results with experiments.

Beyond spectral gap : The role of the topology in decentralized learning

In data-parallel optimization of machine learning models, workers collaborate to improve their estimates of the model: more accurate gradients allow them to use larger learning rates and optimize faster. In the decentralized setting, in which workers communicate over a sparse graph, current theory fails to capture important aspects of real-world behavior. First, the `spectral gap' of the communication graph is not predictive of its empirical performance in (deep) learning. Second, current theory does not explain that collaboration enables larger learning rates than training alone. In fact, it prescribes smaller learning rates, which further decrease as graphs become larger, failing to explain convergence dynamics in infinite graphs. This paper aims to paint an accurate picture of sparsely-connected distributed optimization. We quantify how the graph topology influences convergence in a quadratic toy problem and provide theoretical results for general smooth and (strongly) convex objectives. Our theory matches empirical observations in deep learning, and accurately describes the relative merits of different graph topologies. This paper is an extension of the conference paper by Vogels et. al. (2022). Code: https://github.com/epfml/topology-in-decentralized-learning.

Beyond spectral gap: The role of the topology in decentralized learning

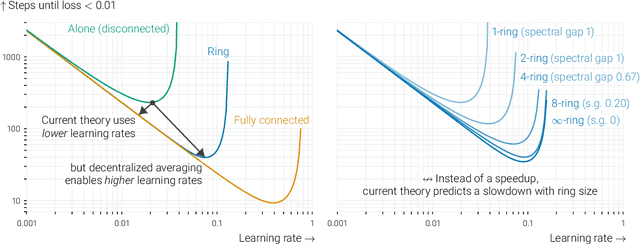
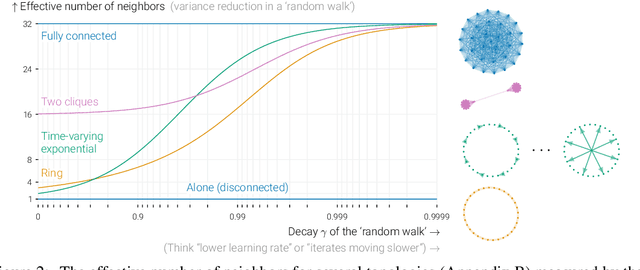
In data-parallel optimization of machine learning models, workers collaborate to improve their estimates of the model: more accurate gradients allow them to use larger learning rates and optimize faster. We consider the setting in which all workers sample from the same dataset, and communicate over a sparse graph (decentralized). In this setting, current theory fails to capture important aspects of real-world behavior. First, the 'spectral gap' of the communication graph is not predictive of its empirical performance in (deep) learning. Second, current theory does not explain that collaboration enables larger learning rates than training alone. In fact, it prescribes smaller learning rates, which further decrease as graphs become larger, failing to explain convergence in infinite graphs. This paper aims to paint an accurate picture of sparsely-connected distributed optimization when workers share the same data distribution. We quantify how the graph topology influences convergence in a quadratic toy problem and provide theoretical results for general smooth and (strongly) convex objectives. Our theory matches empirical observations in deep learning, and accurately describes the relative merits of different graph topologies.

A Continuized View on Nesterov Acceleration for Stochastic Gradient Descent and Randomized Gossip

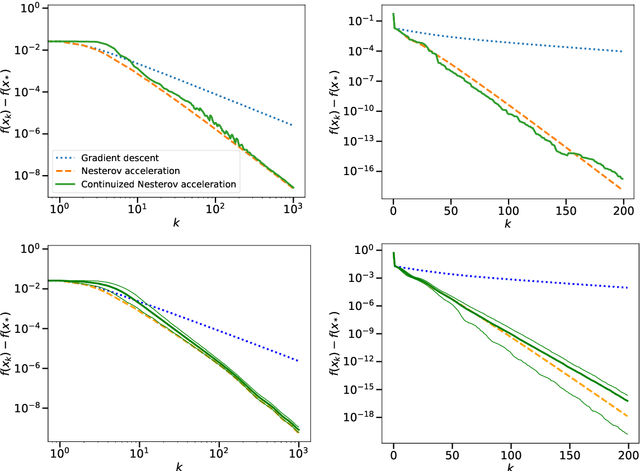
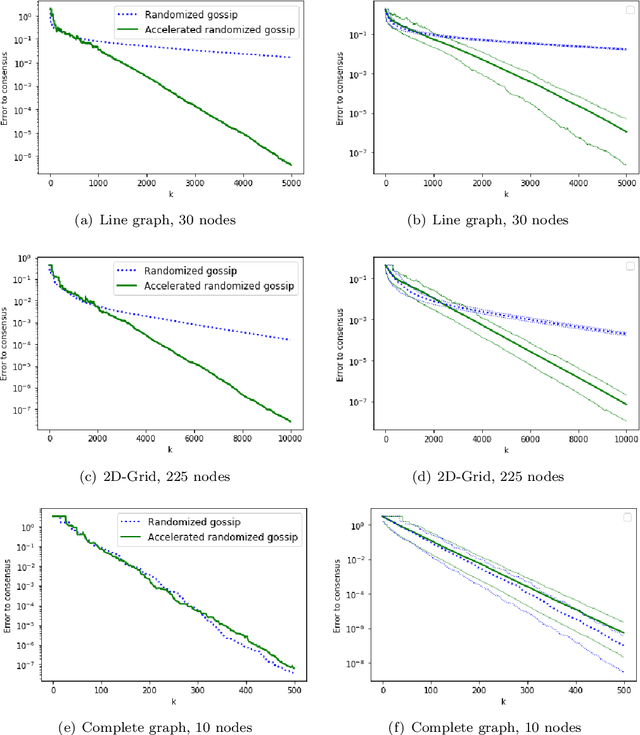
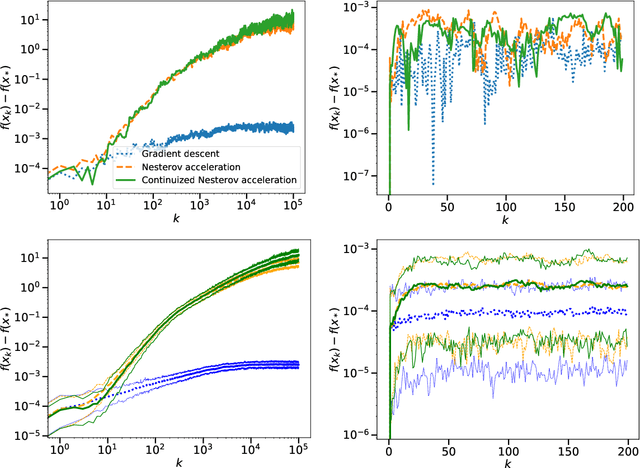
We introduce the continuized Nesterov acceleration, a close variant of Nesterov acceleration whose variables are indexed by a continuous time parameter. The two variables continuously mix following a linear ordinary differential equation and take gradient steps at random times. This continuized variant benefits from the best of the continuous and the discrete frameworks: as a continuous process, one can use differential calculus to analyze convergence and obtain analytical expressions for the parameters; and a discretization of the continuized process can be computed exactly with convergence rates similar to those of Nesterov original acceleration. We show that the discretization has the same structure as Nesterov acceleration, but with random parameters. We provide continuized Nesterov acceleration under deterministic as well as stochastic gradients, with either additive or multiplicative noise. Finally, using our continuized framework and expressing the gossip averaging problem as the stochastic minimization of a certain energy function, we provide the first rigorous acceleration of asynchronous gossip algorithms.

Decentralized Optimization with Heterogeneous Delays: a Continuous-Time Approach

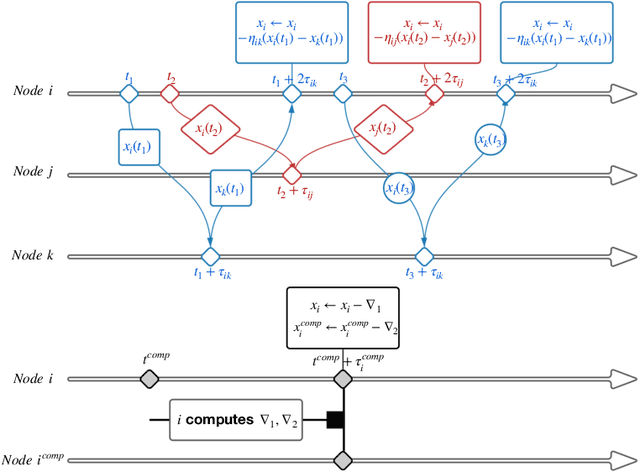
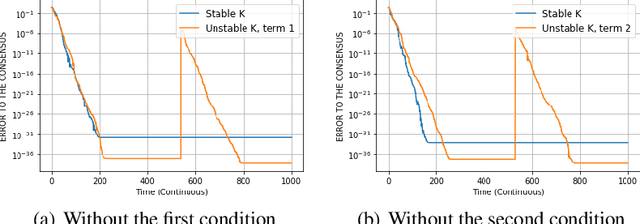
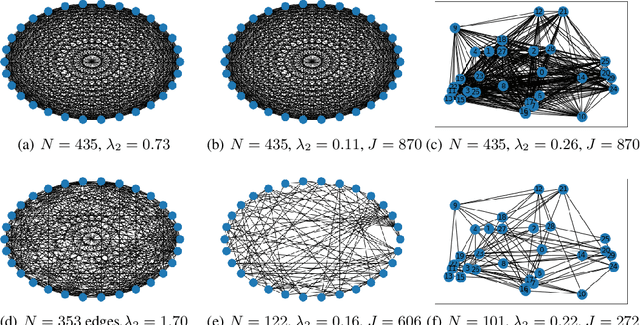
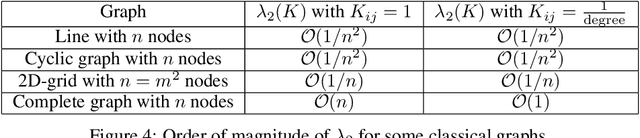
In decentralized optimization, nodes of a communication network privately possess a local objective function, and communicate using gossip-based methods in order to minimize the average of these per-node objectives. While synchronous algorithms can be heavily slowed down by a few nodes and edges in the graph (the straggler problem), their asynchronous counterparts lack from a sharp analysis taking into account heterogeneous delays in the communication network. In this paper, we propose a novel continuous-time framework to analyze asynchronous algorithms, which does not require to define a global ordering of the events, and allows to finely characterize the time complexity in the presence of (heterogeneous) delays. Using this framework, we describe a fully asynchronous decentralized algorithm to minimize the sum of smooth and strongly convex functions. Our algorithm (DCDM, Delayed Coordinate Dual Method), based on delayed randomized gossip communications and local computational updates, achieves an asynchronous speed-up: the rate of convergence is tightly characterized in terms of the eigengap of the graph weighted by local delays only, instead of the global worst-case delays as in previous analyses.

Dynamic Safe Interruptibility for Decentralized Multi-Agent Reinforcement Learning

In reinforcement learning, agents learn by performing actions and observing their outcomes. Sometimes, it is desirable for a human operator to \textit{interrupt} an agent in order to prevent dangerous situations from happening. Yet, as part of their learning process, agents may link these interruptions, that impact their reward, to specific states and deliberately avoid them. The situation is particularly challenging in a multi-agent context because agents might not only learn from their own past interruptions, but also from those of other agents. Orseau and Armstrong defined \emph{safe interruptibility} for one learner, but their work does not naturally extend to multi-agent systems. This paper introduces \textit{dynamic safe interruptibility}, an alternative definition more suited to decentralized learning problems, and studies this notion in two learning frameworks: \textit{joint action learners} and \textit{independent learners}. We give realistic sufficient conditions on the learning algorithm to enable dynamic safe interruptibility in the case of joint action learners, yet show that these conditions are not sufficient for independent learners. We show however that if agents can detect interruptions, it is possible to prune the observations to ensure dynamic safe interruptibility even for independent learners.