Kernel Dynamic Mode Decomposition For Sparse Reconstruction of Closable Koopman Operators

Spatial temporal reconstruction of dynamical system is indeed a crucial problem with diverse applications ranging from climate modeling to numerous chaotic and physical processes. These reconstructions are based on the harmonious relationship between the Koopman operators and the choice of dictionary, determined implicitly by a kernel function. This leads to the approximation of the Koopman operators in a reproducing kernel Hilbert space (RKHS) associated with that kernel function. Data-driven analysis of Koopman operators demands that Koopman operators be closable over the underlying RKHS, which still remains an unsettled, unexplored, and critical operator-theoretic challenge. We aim to address this challenge by investigating the embedding of the Laplacian kernel in the measure-theoretic sense, giving rise to a rich enough RKHS to settle the closability of the Koopman operators. We leverage Kernel Extended Dynamic Mode Decomposition with the Laplacian kernel to reconstruct the dominant spatial temporal modes of various diverse dynamical systems. After empirical demonstration, we concrete such results by providing the theoretical justification leveraging the closability of the Koopman operators on the RKHS generated by the Laplacian kernel on the avenues of Koopman mode decomposition and the Koopman spectral measure. Such results were explored from both grounds of operator theory and data-driven science, thus making the Laplacian kernel a robust choice for spatial-temporal reconstruction.

Liouville Flow Importance Sampler

We present the Liouville Flow Importance Sampler (LFIS), an innovative flow-based model for generating samples from unnormalized density functions. LFIS learns a time-dependent velocity field that deterministically transports samples from a simple initial distribution to a complex target distribution, guided by a prescribed path of annealed distributions. The training of LFIS utilizes a unique method that enforces the structure of a derived partial differential equation to neural networks modeling velocity fields. By considering the neural velocity field as an importance sampler, sample weights can be computed through accumulating errors along the sample trajectories driven by neural velocity fields, ensuring unbiased and consistent estimation of statistical quantities. We demonstrate the effectiveness of LFIS through its application to a range of benchmark problems, on many of which LFIS achieved state-of-the-art performance.

Semi-supervised Learning of Pushforwards For Domain Translation & Adaptation

Given two probability densities on related data spaces, we seek a map pushing one density to the other while satisfying application-dependent constraints. For maps to have utility in a broad application space (including domain translation, domain adaptation, and generative modeling), the map must be available to apply on out-of-sample data points and should correspond to a probabilistic model over the two spaces. Unfortunately, existing approaches, which are primarily based on optimal transport, do not address these needs. In this paper, we introduce a novel pushforward map learning algorithm that utilizes normalizing flows to parameterize the map. We first re-formulate the classical optimal transport problem to be map-focused and propose a learning algorithm to select from all possible maps under the constraint that the map minimizes a probability distance and application-specific regularizers; thus, our method can be seen as solving a modified optimal transport problem. Once the map is learned, it can be used to map samples from a source domain to a target domain. In addition, because the map is parameterized as a composition of normalizing flows, it models the empirical distributions over the two data spaces and allows both sampling and likelihood evaluation for both data sets. We compare our method (parOT) to related optimal transport approaches in the context of domain adaptation and domain translation on benchmark data sets. Finally, to illustrate the impact of our work on applied problems, we apply parOT to a real scientific application: spectral calibration for high-dimensional measurements from two vastly different environments

Generative structured normalizing flow Gaussian processes applied to spectroscopic data

In this work, we propose a novel generative model for mapping inputs to structured, high-dimensional outputs using structured conditional normalizing flows and Gaussian process regression. The model is motivated by the need to characterize uncertainty in the input/output relationship when making inferences on new data. In particular, in the physical sciences, limited training data may not adequately characterize future observed data; it is critical that models adequately indicate uncertainty, particularly when they may be asked to extrapolate. In our proposed model, structured conditional normalizing flows provide parsimonious latent representations that relate to the inputs through a Gaussian process, providing exact likelihood calculations and uncertainty that naturally increases away from the training data inputs. We demonstrate the methodology on laser-induced breakdown spectroscopy data from the ChemCam instrument onboard the Mars rover Curiosity. ChemCam was designed to recover the chemical composition of rock and soil samples by measuring the spectral properties of plasma atomic emissions induced by a laser pulse. We show that our model can generate realistic spectra conditional on a given chemical composition and that we can use the model to perform uncertainty quantification of chemical compositions for new observed spectra. Based on our results, we anticipate that our proposed modeling approach may be useful in other scientific domains with high-dimensional, complex structure where it is important to quantify predictive uncertainty.

BB-ML: Basic Block Performance Prediction using Machine Learning Techniques

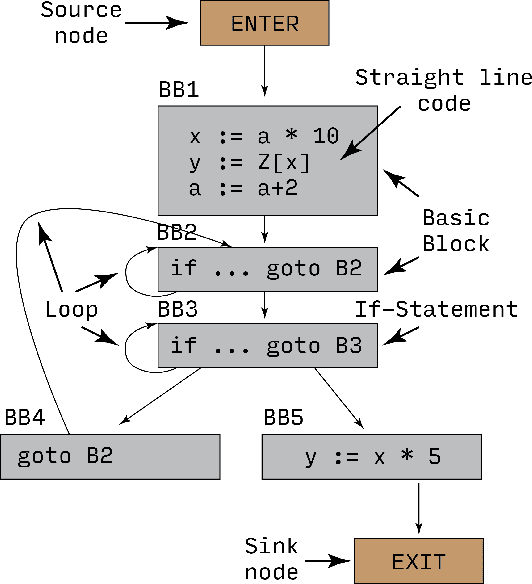
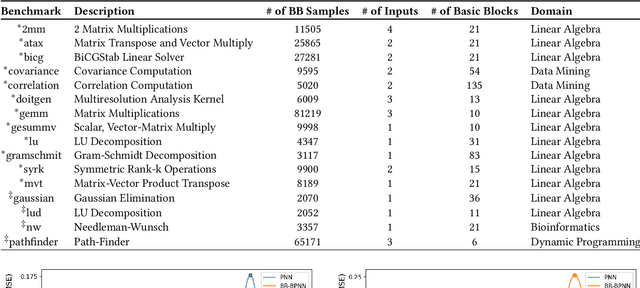
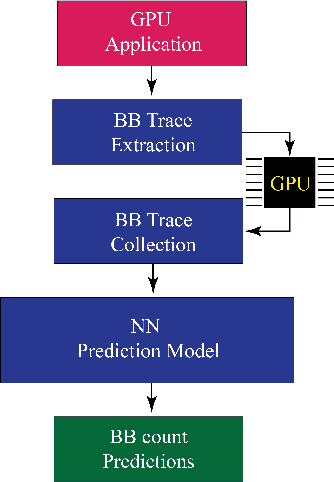
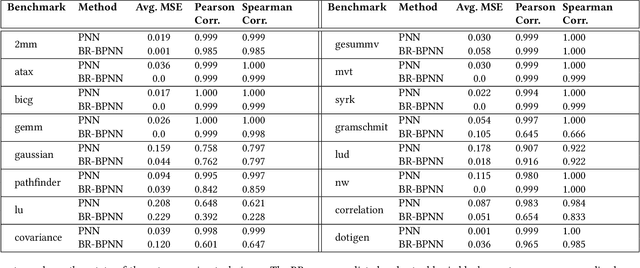
Recent years have seen the adoption of Machine Learning (ML) techniques to predict the performance of large-scale applications, mostly at a coarse level. In contrast, we propose to use ML techniques for performance prediction at much finer granularity, namely at the levels of Basic Block (BB), which are the single entry-single exit code blocks that are used as analysis tools by all compilers to break down a large code into manageable pieces. Utilizing ML and BB analysis together can enable scalable hardware-software co-design beyond the current state of the art. In this work, we extrapolate the basic block execution counts of GPU applications for large inputs sizes from the counts of smaller input sizes of the same application. We employ two ML models, a Poisson Neural Network (PNN) and a Bayesian Regularization Backpropagation Neural Network (BR-BPNN). We train both models using the lowest input values of the application and random input values to predict basic block counts. Results show that our models accurately predict the basic block execution counts of 16 benchmark applications. For PNN and BR-BPNN models, we achieve an average accuracy of 93.5% and 95.6%, respectively, while extrapolating the basic block counts for large input sets when the model is trained using smaller input sets. Additionally, the models show an average accuracy of 97.7% and 98.1%, respectively, while predicting basic block counts on random instances.

Neural density estimation and uncertainty quantification for laser induced breakdown spectroscopy spectra

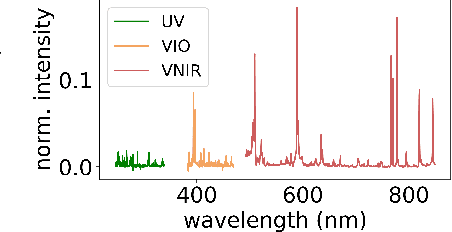
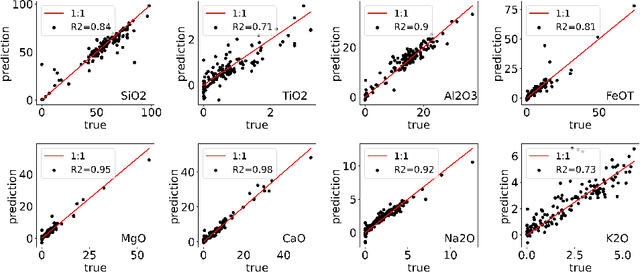
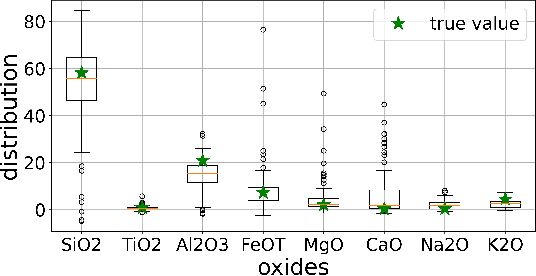
Constructing probability densities for inference in high-dimensional spectral data is often intractable. In this work, we use normalizing flows on structured spectral latent spaces to estimate such densities, enabling downstream inference tasks. In addition, we evaluate a method for uncertainty quantification when predicting unobserved state vectors associated with each spectrum. We demonstrate the capability of this approach on laser-induced breakdown spectroscopy data collected by the ChemCam instrument on the Mars rover Curiosity. Using our approach, we are able to generate realistic spectral samples and to accurately predict state vectors with associated well-calibrated uncertainties. We anticipate that this methodology will enable efficient probabilistic modeling of spectral data, leading to potential advances in several areas, including out-of-distribution detection and sensitivity analysis.

StressNet: Deep Learning to Predict Stress With Fracture Propagation in Brittle Materials

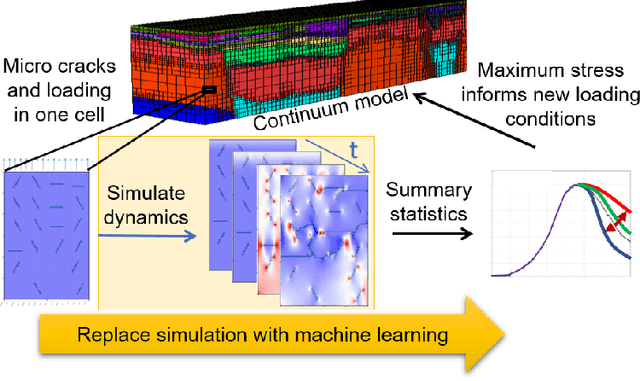
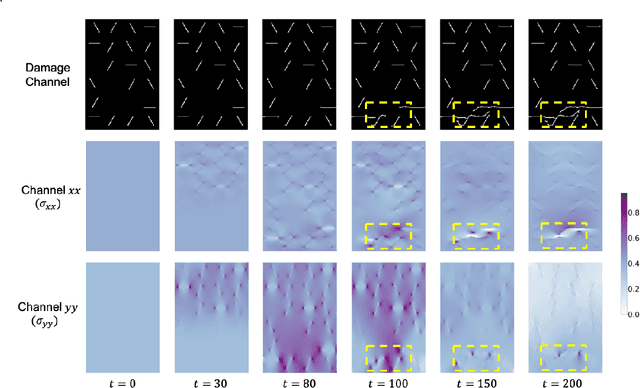
Catastrophic failure in brittle materials is often due to the rapid growth and coalescence of cracks aided by high internal stresses. Hence, accurate prediction of maximum internal stress is critical to predicting time to failure and improving the fracture resistance and reliability of materials. Existing high-fidelity methods, such as the Finite-Discrete Element Model (FDEM), are limited by their high computational cost. Therefore, to reduce computational cost while preserving accuracy, a novel deep learning model, "StressNet," is proposed to predict the entire sequence of maximum internal stress based on fracture propagation and the initial stress data. More specifically, the Temporal Independent Convolutional Neural Network (TI-CNN) is designed to capture the spatial features of fractures like fracture path and spall regions, and the Bidirectional Long Short-term Memory (Bi-LSTM) Network is adapted to capture the temporal features. By fusing these features, the evolution in time of the maximum internal stress can be accurately predicted. Moreover, an adaptive loss function is designed by dynamically integrating the Mean Squared Error (MSE) and the Mean Absolute Percentage Error (MAPE), to reflect the fluctuations in maximum internal stress. After training, the proposed model is able to compute accurate multi-step predictions of maximum internal stress in approximately 20 seconds, as compared to the FDEM run time of 4 hours, with an average MAPE of 2% relative to test data.