Regularization via f-Divergence: An Application to Multi-Oxide Spectroscopic Analysis

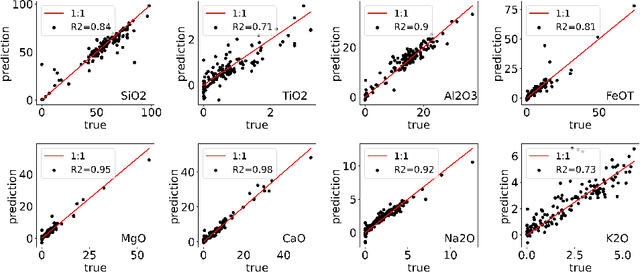
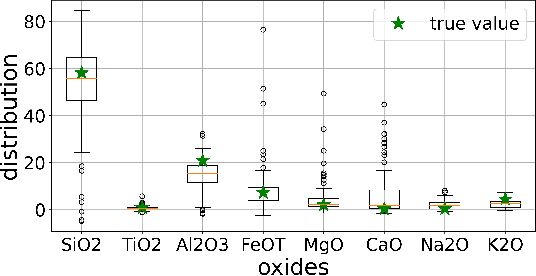
In this paper, we address the task of characterizing the chemical composition of planetary surfaces using convolutional neural networks (CNNs). Specifically, we seek to predict the multi-oxide weights of rock samples based on spectroscopic data collected under Martian conditions. We frame this problem as a multi-target regression task and propose a novel regularization method based on f-divergence. The f-divergence regularization is designed to constrain the distributional discrepancy between predictions and noisy targets. This regularizer serves a dual purpose: on the one hand, it mitigates overfitting by enforcing a constraint on the distributional difference between predictions and noisy targets. On the other hand, it acts as an auxiliary loss function, penalizing the neural network when the divergence between the predicted and target distributions becomes too large. To enable backpropagation during neural network training, we develop a differentiable f-divergence and incorporate it into the f-divergence regularization, making the network training feasible. We conduct experiments using spectra collected in a Mars-like environment by the remote-sensing instruments aboard the Curiosity and Perseverance rovers. Experimental results on multi-oxide weight prediction demonstrate that the proposed $f$-divergence regularization performs better than or comparable to standard regularization methods including $L_1$, $L_2$, and dropout. Notably, combining the $f$-divergence regularization with these standard regularization further enhances performance, outperforming each regularization method used independently.

Semi-supervised Learning of Pushforwards For Domain Translation & Adaptation

Given two probability densities on related data spaces, we seek a map pushing one density to the other while satisfying application-dependent constraints. For maps to have utility in a broad application space (including domain translation, domain adaptation, and generative modeling), the map must be available to apply on out-of-sample data points and should correspond to a probabilistic model over the two spaces. Unfortunately, existing approaches, which are primarily based on optimal transport, do not address these needs. In this paper, we introduce a novel pushforward map learning algorithm that utilizes normalizing flows to parameterize the map. We first re-formulate the classical optimal transport problem to be map-focused and propose a learning algorithm to select from all possible maps under the constraint that the map minimizes a probability distance and application-specific regularizers; thus, our method can be seen as solving a modified optimal transport problem. Once the map is learned, it can be used to map samples from a source domain to a target domain. In addition, because the map is parameterized as a composition of normalizing flows, it models the empirical distributions over the two data spaces and allows both sampling and likelihood evaluation for both data sets. We compare our method (parOT) to related optimal transport approaches in the context of domain adaptation and domain translation on benchmark data sets. Finally, to illustrate the impact of our work on applied problems, we apply parOT to a real scientific application: spectral calibration for high-dimensional measurements from two vastly different environments

Generative structured normalizing flow Gaussian processes applied to spectroscopic data

In this work, we propose a novel generative model for mapping inputs to structured, high-dimensional outputs using structured conditional normalizing flows and Gaussian process regression. The model is motivated by the need to characterize uncertainty in the input/output relationship when making inferences on new data. In particular, in the physical sciences, limited training data may not adequately characterize future observed data; it is critical that models adequately indicate uncertainty, particularly when they may be asked to extrapolate. In our proposed model, structured conditional normalizing flows provide parsimonious latent representations that relate to the inputs through a Gaussian process, providing exact likelihood calculations and uncertainty that naturally increases away from the training data inputs. We demonstrate the methodology on laser-induced breakdown spectroscopy data from the ChemCam instrument onboard the Mars rover Curiosity. ChemCam was designed to recover the chemical composition of rock and soil samples by measuring the spectral properties of plasma atomic emissions induced by a laser pulse. We show that our model can generate realistic spectra conditional on a given chemical composition and that we can use the model to perform uncertainty quantification of chemical compositions for new observed spectra. Based on our results, we anticipate that our proposed modeling approach may be useful in other scientific domains with high-dimensional, complex structure where it is important to quantify predictive uncertainty.

Denoising neural networks for magnetic resonance spectroscopy

In many scientific applications, measured time series are corrupted by noise or distortions. Traditional denoising techniques often fail to recover the signal of interest, particularly when the signal-to-noise ratio is low or when certain assumptions on the signal and noise are violated. In this work, we demonstrate that deep learning-based denoising methods can outperform traditional techniques while exhibiting greater robustness to variation in noise and signal characteristics. Our motivating example is magnetic resonance spectroscopy, in which a primary goal is to detect the presence of short-duration, low-amplitude radio frequency signals that are often obscured by strong interference that can be difficult to separate from the signal using traditional methods. We explore various deep learning architecture choices to capture the inherently complex-valued nature of magnetic resonance signals. On both synthetic and experimental data, we show that our deep learning-based approaches can exceed performance of traditional techniques, providing a powerful new class of methods for analysis of scientific time series data.

Neural density estimation and uncertainty quantification for laser induced breakdown spectroscopy spectra

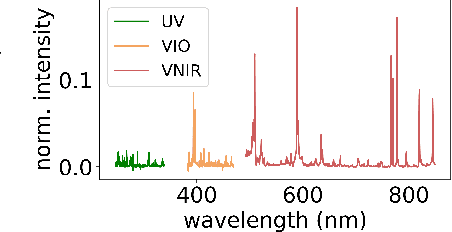
Constructing probability densities for inference in high-dimensional spectral data is often intractable. In this work, we use normalizing flows on structured spectral latent spaces to estimate such densities, enabling downstream inference tasks. In addition, we evaluate a method for uncertainty quantification when predicting unobserved state vectors associated with each spectrum. We demonstrate the capability of this approach on laser-induced breakdown spectroscopy data collected by the ChemCam instrument on the Mars rover Curiosity. Using our approach, we are able to generate realistic spectral samples and to accurately predict state vectors with associated well-calibrated uncertainties. We anticipate that this methodology will enable efficient probabilistic modeling of spectral data, leading to potential advances in several areas, including out-of-distribution detection and sensitivity analysis.

Torus Graphs for Multivariate Phase Coupling Analysis

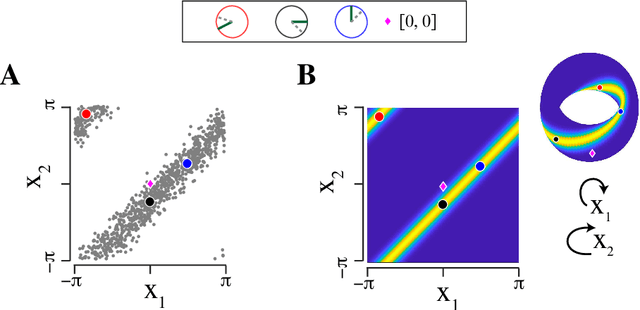
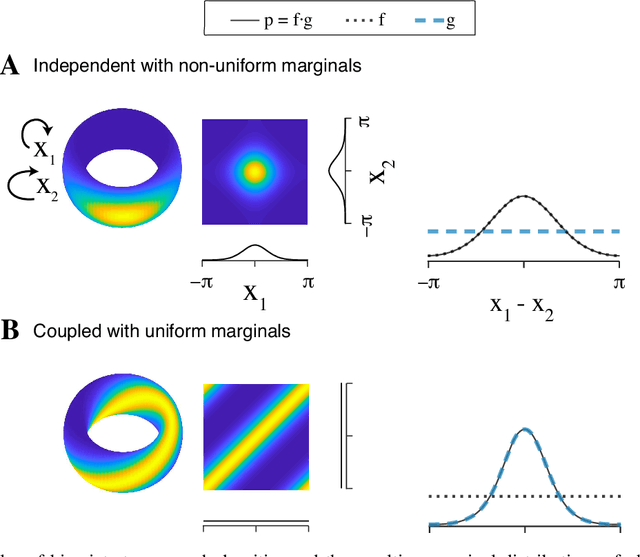
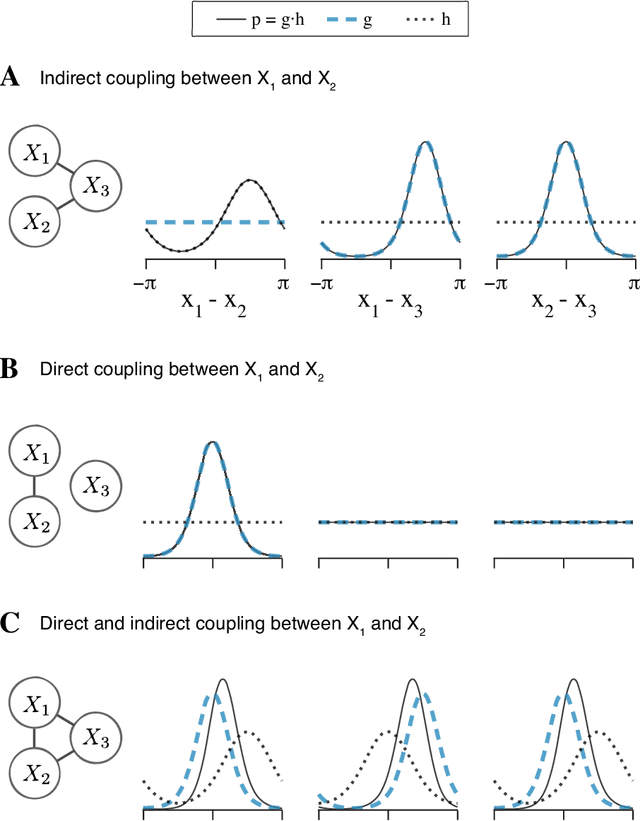
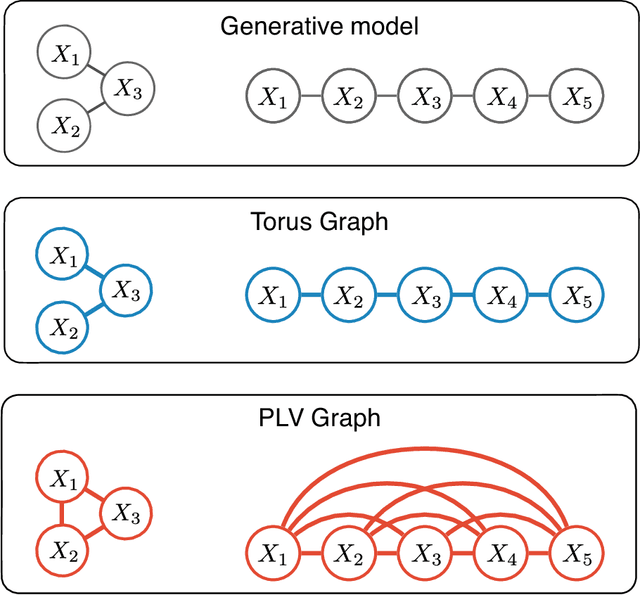
Angular measurements are often modeled as circular random variables, where there are natural circular analogues of moments, including correlation. Because a product of circles is a torus, a d-dimensional vector of circular random variables lies on a d-dimensional torus. For such vectors we present here a class of graphical models, which we call torus graphs, based on the full exponential family with pairwise interactions. The topological distinction between a torus and Euclidean space has several important consequences. Our development was motivated by the problem of identifying phase coupling among oscillatory signals recorded from multiple electrodes in the brain: oscillatory phases across electrodes might tend to advance or recede together, indicating coordination across brain areas. The data analyzed here consisted of 24 phase angles measured repeatedly across 840 experimental trials (replications) during a memory task, where the electrodes were in 4 distinct brain regions, all known to be active while memories are being stored or retrieved. In realistic numerical simulations, we found that a standard pairwise assessment, known as phase locking value, is unable to describe multivariate phase interactions, but that torus graphs can accurately identify conditional associations. Torus graphs generalize several more restrictive approaches that have appeared in various scientific literatures, and produced intuitive results in the data we analyzed. Torus graphs thus unify multivariate analysis of circular data and present fertile territory for future research.