Differentiable IFS Fractals

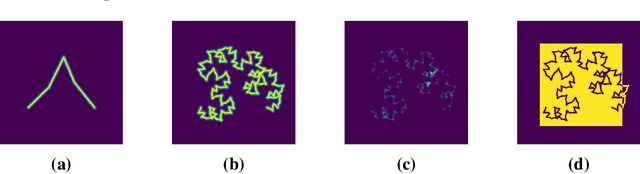
I present my explorations in rendering Iterated Function System (IFS) fractals using a differentiable rendering pipeline. Differentiable rendering is a recent innovation at the intersection of graphics and machine learning. This opens up many possibilities for generating fractals that meet particular criteria. In this paper I show how my method can be used to generate an IFS fractal that resembles a target image.

Diff2Dist: Learning Spectrally Distinct Edge Functions, with Applications to Cell Morphology Analysis

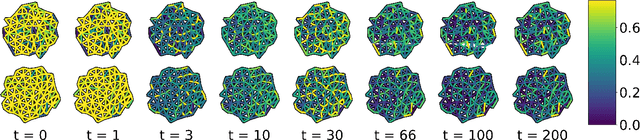
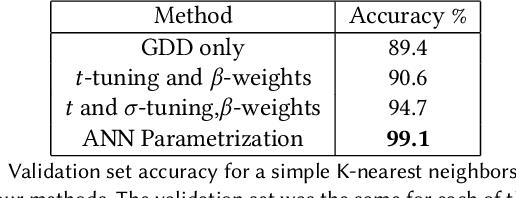
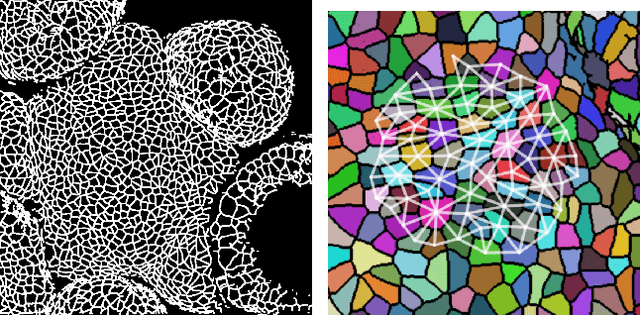
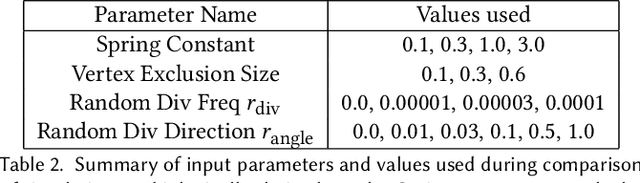
We present a method for learning "spectrally descriptive" edge weights for graphs. We generalize a previously known distance measure on graphs (Graph Diffusion Distance), thereby allowing it to be tuned to minimize an arbitrary loss function. Because all steps involved in calculating this modified GDD are differentiable, we demonstrate that it is possible for a small neural network model to learn edge weights which minimize loss. GDD alone does not effectively discriminate between graphs constructed from shoot apical meristem images of wild-type vs. mutant \emph{Arabidopsis thaliana} specimens. However, training edge weights and kernel parameters with contrastive loss produces a learned distance metric with large margins between these graph categories. We demonstrate this by showing improved performance of a simple k-nearest-neighbors classifier on the learned distance matrix. We also demonstrate a further application of this method to biological image analysis: once trained, we use our model to compute the distance between the biological graphs and a set of graphs output by a cell division simulator. This allows us to identify simulation parameter regimes which are similar to each class of graph in our original dataset.

StressNet: Deep Learning to Predict Stress With Fracture Propagation in Brittle Materials

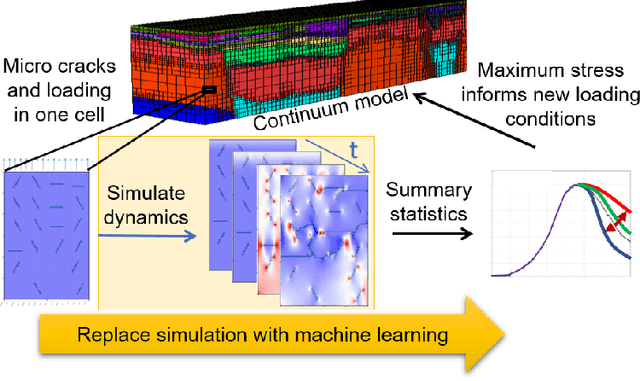
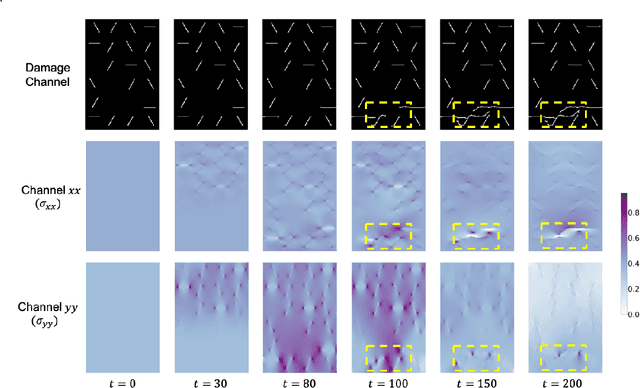
Catastrophic failure in brittle materials is often due to the rapid growth and coalescence of cracks aided by high internal stresses. Hence, accurate prediction of maximum internal stress is critical to predicting time to failure and improving the fracture resistance and reliability of materials. Existing high-fidelity methods, such as the Finite-Discrete Element Model (FDEM), are limited by their high computational cost. Therefore, to reduce computational cost while preserving accuracy, a novel deep learning model, "StressNet," is proposed to predict the entire sequence of maximum internal stress based on fracture propagation and the initial stress data. More specifically, the Temporal Independent Convolutional Neural Network (TI-CNN) is designed to capture the spatial features of fractures like fracture path and spall regions, and the Bidirectional Long Short-term Memory (Bi-LSTM) Network is adapted to capture the temporal features. By fusing these features, the evolution in time of the maximum internal stress can be accurately predicted. Moreover, an adaptive loss function is designed by dynamically integrating the Mean Squared Error (MSE) and the Mean Absolute Percentage Error (MAPE), to reflect the fluctuations in maximum internal stress. After training, the proposed model is able to compute accurate multi-step predictions of maximum internal stress in approximately 20 seconds, as compared to the FDEM run time of 4 hours, with an average MAPE of 2% relative to test data.