High Dimensional Data Decomposition for Anomaly Detection of Textured Images

In the realm of diverse high-dimensional data, images play a significant role across various processes of manufacturing systems where efficient image anomaly detection has emerged as a core technology of utmost importance. However, when applied to textured defect images, conventional anomaly detection methods have limitations including non-negligible misidentification, low robustness, and excessive reliance on large-scale and structured datasets. This paper proposes a texture basis integrated smooth decomposition (TBSD) approach, which is targeted at efficient anomaly detection in textured images with smooth backgrounds and sparse anomalies. Mathematical formulation of quasi-periodicity and its theoretical properties are investigated for image texture estimation. TBSD method consists of two principal processes: the first process learns the texture basis functions to effectively extract quasi-periodic texture patterns; the subsequent anomaly detection process utilizes that texture basis as prior knowledge to prevent texture misidentification and capture potential anomalies with high accuracy.The proposed method surpasses benchmarks with less misidentification, smaller training dataset requirement, and superior anomaly detection performance on both simulation and real-world datasets.

R^2-HGP: A Double-Regularized Gaussian Process for Heterogeneous Transfer Learning

Multi-output Gaussian process (MGP) models have attracted significant attention for their flexibility and uncertainty-quantification capabilities, and have been widely adopted in multi-source transfer learning scenarios due to their ability to capture inter-task correlations. However, they still face several challenges in transfer learning. First, the input spaces of the source and target domains are often heterogeneous, which makes direct knowledge transfer difficult. Second, potential prior knowledge and physical information are typically ignored during heterogeneous transfer, hampering the utilization of domain-specific insights and leading to unstable mappings. Third, inappropriate information sharing among target and sources can easily lead to negative transfer. Traditional models fail to address these issues in a unified way. To overcome these limitations, this paper proposes a Double-Regularized Heterogeneous Gaussian Process framework (R^2-HGP). Specifically, a trainable prior probability mapping model is first proposed to align the heterogeneous input domains. The resulting aligned inputs are treated as latent variables, upon which a multi-source transfer GP model is constructed and the entire structure is integrated into a novel conditional variational autoencoder (CVAE) based framework. Physical insights is further incorporated as a regularization term to ensure that the alignment results adhere to known physical knowledge. Next, within the multi-source transfer GP model, a sparsity penalty is imposed on the transfer coefficients, enabling the model to adaptively select the most informative source outputs and suppress negative transfer. Extensive simulations and real-world engineering case studies validate the effectiveness of our R^2-HGP, demonstrating consistent superiority over state-of-the-art benchmarks across diverse evaluation metrics.

Spatiotemporal Predictions of Toxic Urban Plumes Using Deep Learning

Industrial accidents, chemical spills, and structural fires can release large amounts of harmful materials that disperse into urban atmospheres and impact populated areas. Computer models are typically used to predict the transport of toxic plumes by solving fluid dynamical equations. However, these models can be computationally expensive due to the need for many grid cells to simulate turbulent flow and resolve individual buildings and streets. In emergency response situations, alternative methods are needed that can run quickly and adequately capture important spatiotemporal features. Here, we present a novel deep learning model called ST-GasNet that was inspired by the mathematical equations that govern the behavior of plumes as they disperse through the atmosphere. ST-GasNet learns the spatiotemporal dependencies from a limited set of temporal sequences of ground-level toxic urban plumes generated by a high-resolution large eddy simulation model. On independent sequences, ST-GasNet accurately predicts the late-time spatiotemporal evolution, given the early-time behavior as an input, even for cases when a building splits a large plume into smaller plumes. By incorporating large-scale wind boundary condition information, ST-GasNet achieves a prediction accuracy of at least 90% on test data for the entire prediction period.

Advancing Additive Manufacturing through Deep Learning: A Comprehensive Review of Current Progress and Future Challenges

Additive manufacturing (AM) has already proved itself to be the potential alternative to widely-used subtractive manufacturing due to its extraordinary capacity of manufacturing highly customized products with minimum material wastage. Nevertheless, it is still not being considered as the primary choice for the industry due to some of its major inherent challenges, including complex and dynamic process interactions, which are sometimes difficult to fully understand even with traditional machine learning because of the involvement of high-dimensional data such as images, point clouds, and voxels. However, the recent emergence of deep learning (DL) is showing great promise in overcoming many of these challenges as DL can automatically capture complex relationships from high-dimensional data without hand-crafted feature extraction. Therefore, the volume of research in the intersection of AM and DL is exponentially growing each year which makes it difficult for the researchers to keep track of the trend and future potential directions. Furthermore, to the best of our knowledge, there is no comprehensive review paper in this research track summarizing the recent studies. Therefore, this paper reviews the recent studies that apply DL for making the AM process better with a high-level summary of their contributions and limitations. Finally, it summarizes the current challenges and recommends some of the promising opportunities in this domain for further investigation with a special focus on generalizing DL models for wide-range of geometry types, managing uncertainties both in AM data and DL models, overcoming limited and noisy AM data issues by incorporating generative models, and unveiling the potential of interpretable DL for AM.

Coverage Path Planning for Robotic Quality Inspection with Control on Measurement Uncertainty

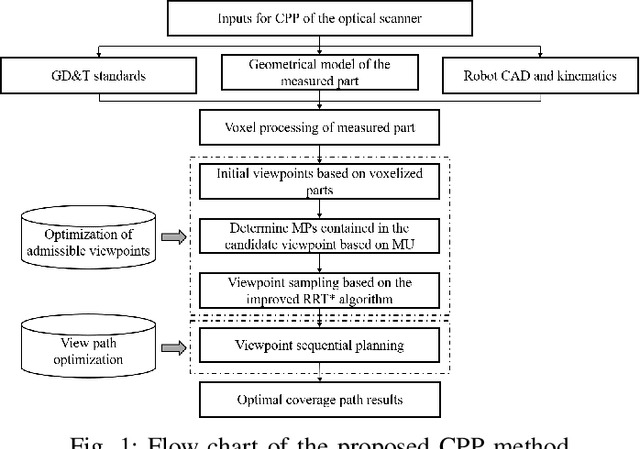
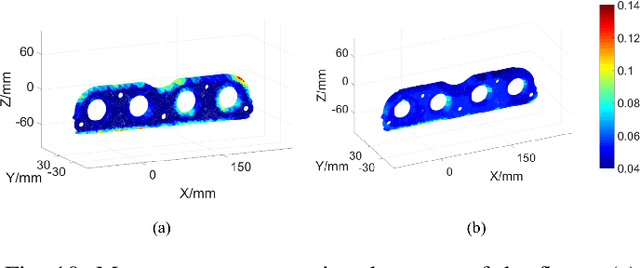
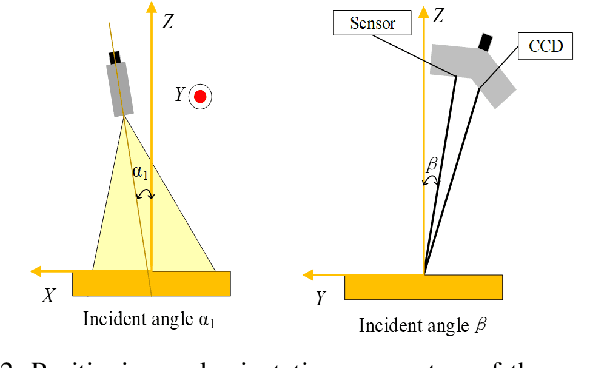
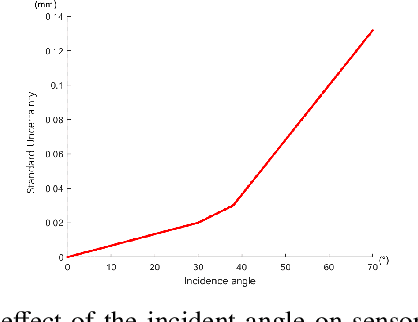
The optical scanning gauges mounted on the robots are commonly used in quality inspection, such as verifying the dimensional specification of sheet structures. Coverage path planning (CPP) significantly influences the accuracy and efficiency of robotic quality inspection. Traditional CPP strategies focus on minimizing the number of viewpoints or traveling distance of robots under the condition of full coverage inspection. The measurement uncertainty when collecting the scanning data is less considered in the free-form surface inspection. To address this problem, a novel CPP method with the optimal viewpoint sampling strategy is proposed to incorporate the measurement uncertainty of key measurement points (MPs) into free-form surface inspection. At first, the feasible ranges of measurement uncertainty are calculated based on the tolerance specifications of the MPs. The initial feasible viewpoint set is generated considering the measurement uncertainty and the visibility of MPs. Then, the inspection cost function is built to evaluate the number of selected viewpoints and the average measurement uncertainty in the field of views (FOVs) of all the selected viewpoints. Afterward, an enhanced rapidly-exploring random tree (RRT*) algorithm is proposed for viewpoint sampling using the inspection cost function and CPP optimization. Case studies, including simulation tests and inspection experiments, have been conducted to evaluate the effectiveness of the proposed method. Results show that the scanning precision of key MPs is significantly improved compared with the benchmark method.

WOOD: Wasserstein-based Out-of-Distribution Detection

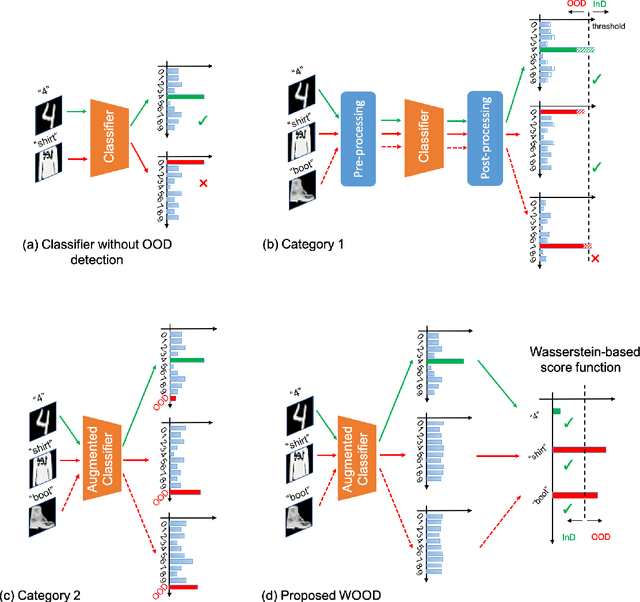
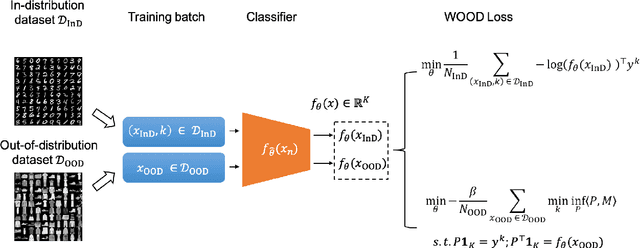
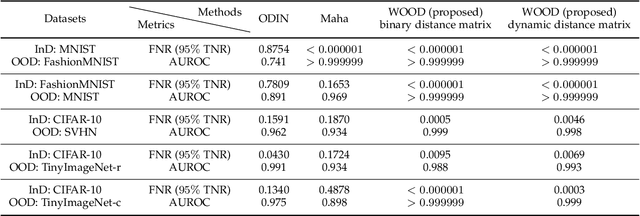
The training and test data for deep-neural-network-based classifiers are usually assumed to be sampled from the same distribution. When part of the test samples are drawn from a distribution that is sufficiently far away from that of the training samples (a.k.a. out-of-distribution (OOD) samples), the trained neural network has a tendency to make high confidence predictions for these OOD samples. Detection of the OOD samples is critical when training a neural network used for image classification, object detection, etc. It can enhance the classifier's robustness to irrelevant inputs, and improve the system resilience and security under different forms of attacks. Detection of OOD samples has three main challenges: (i) the proposed OOD detection method should be compatible with various architectures of classifiers (e.g., DenseNet, ResNet), without significantly increasing the model complexity and requirements on computational resources; (ii) the OOD samples may come from multiple distributions, whose class labels are commonly unavailable; (iii) a score function needs to be defined to effectively separate OOD samples from in-distribution (InD) samples. To overcome these challenges, we propose a Wasserstein-based out-of-distribution detection (WOOD) method. The basic idea is to define a Wasserstein-distance-based score that evaluates the dissimilarity between a test sample and the distribution of InD samples. An optimization problem is then formulated and solved based on the proposed score function. The statistical learning bound of the proposed method is investigated to guarantee that the loss value achieved by the empirical optimizer approximates the global optimum. The comparison study results demonstrate that the proposed WOOD consistently outperforms other existing OOD detection methods.

Failure-averse Active Learning for Physics-constrained Systems

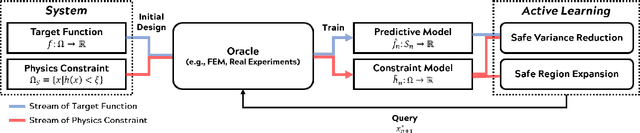
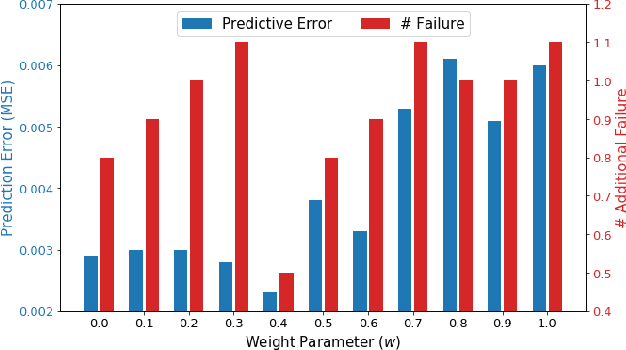
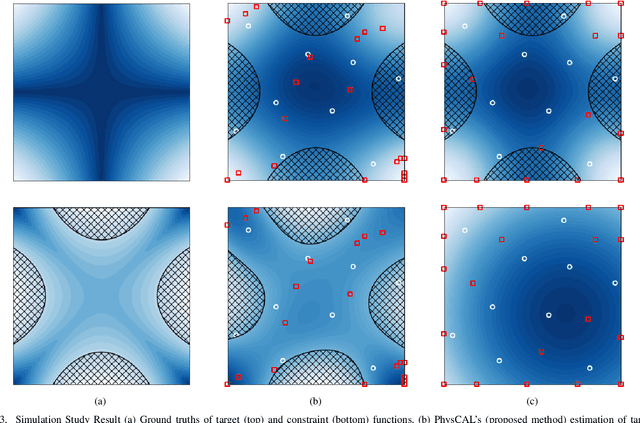
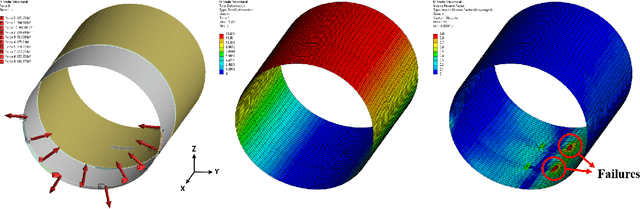
Active learning is a subfield of machine learning that is devised for design and modeling of systems with highly expensive sampling costs. Industrial and engineering systems are generally subject to physics constraints that may induce fatal failures when they are violated, while such constraints are frequently underestimated in active learning. In this paper, we develop a novel active learning method that avoids failures considering implicit physics constraints that govern the system. The proposed approach is driven by two tasks: the safe variance reduction explores the safe region to reduce the variance of the target model, and the safe region expansion aims to extend the explorable region exploiting the probabilistic model of constraints. The global acquisition function is devised to judiciously optimize acquisition functions of two tasks, and its theoretical properties are provided. The proposed method is applied to the composite fuselage assembly process with consideration of material failure using the Tsai-wu criterion, and it is able to achieve zero-failure without the knowledge of explicit failure regions.

A Robust Asymmetric Kernel Function for Bayesian Optimization, with Application to Image Defect Detection in Manufacturing Systems

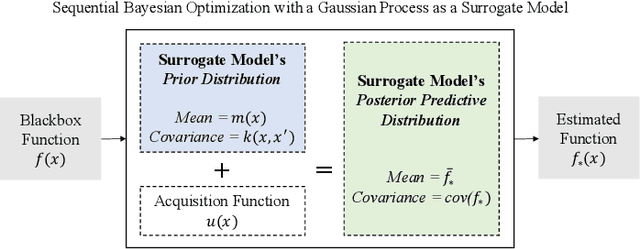
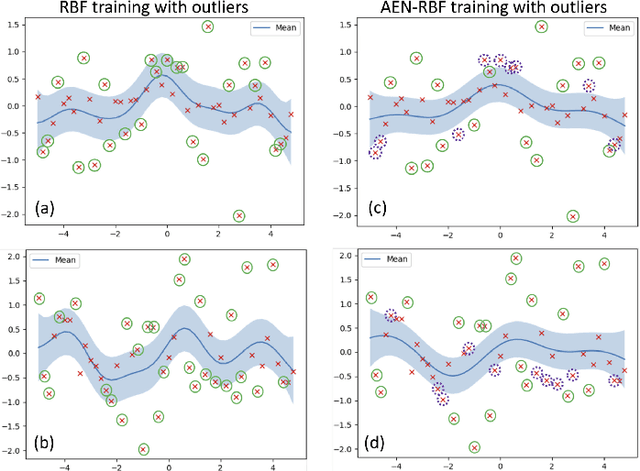
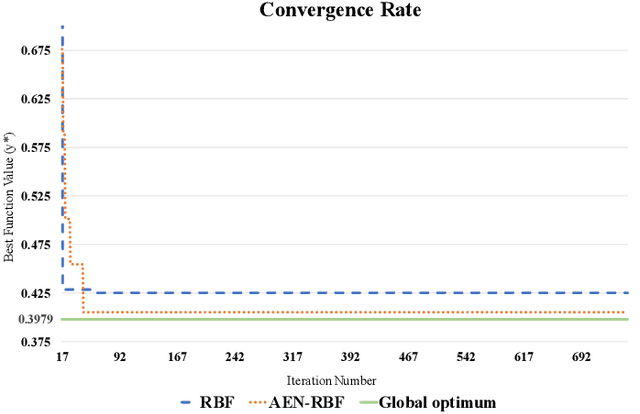
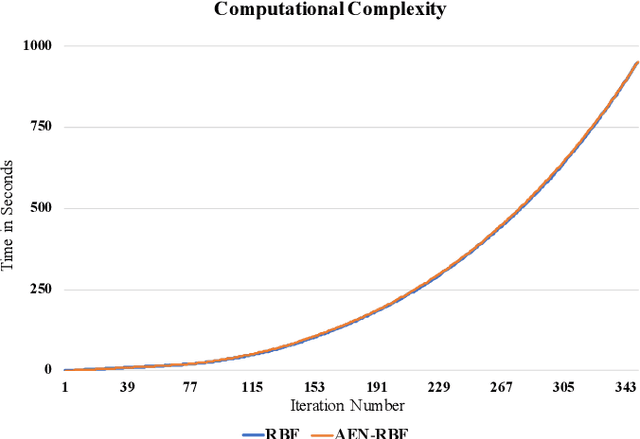
Some response surface functions in complex engineering systems are usually highly nonlinear, unformed, and expensive-to-evaluate. To tackle this challenge, Bayesian optimization, which conducts sequential design via a posterior distribution over the objective function, is a critical method used to find the global optimum of black-box functions. Kernel functions play an important role in shaping the posterior distribution of the estimated function. The widely used kernel function, e.g., radial basis function (RBF), is very vulnerable and susceptible to outliers; the existence of outliers is causing its Gaussian process surrogate model to be sporadic. In this paper, we propose a robust kernel function, Asymmetric Elastic Net Radial Basis Function (AEN-RBF). Its validity as a kernel function and computational complexity are evaluated. When compared to the baseline RBF kernel, we prove theoretically that AEN-RBF can realize smaller mean squared prediction error under mild conditions. The proposed AEN-RBF kernel function can also realize faster convergence to the global optimum. We also show that the AEN-RBF kernel function is less sensitive to outliers, and hence improves the robustness of the corresponding Bayesian optimization with Gaussian processes. Through extensive evaluations carried out on synthetic and real-world optimization problems, we show that AEN-RBF outperforms existing benchmark kernel functions.

Task Allocation and Coordinated Motion Planning for Autonomous Multi-Robot Optical Inspection Systems

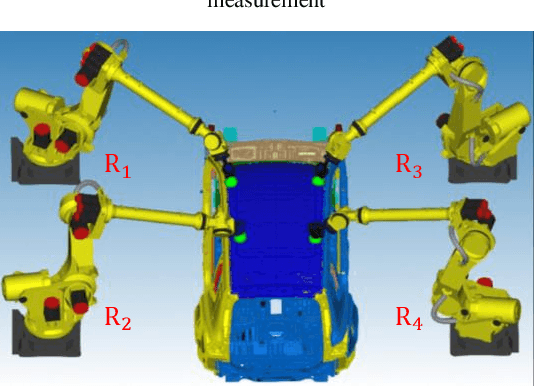
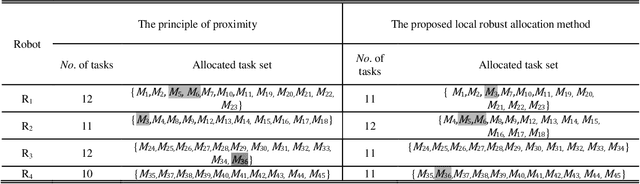
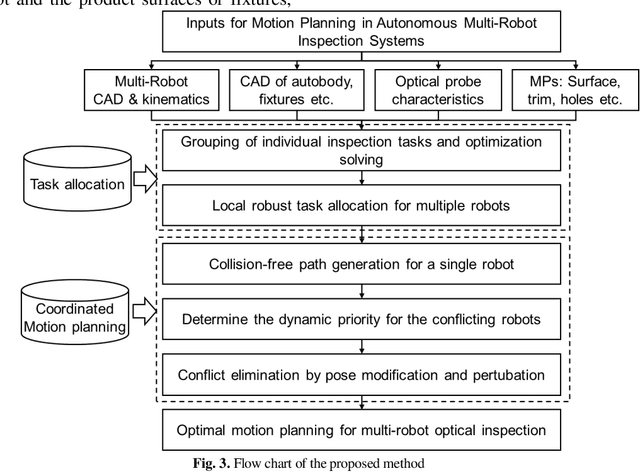
Autonomous multi-robot optical inspection systems are increasingly applied for obtaining inline measurements in process monitoring and quality control. Numerous methods for path planning and robotic coordination have been developed for static and dynamic environments and applied to different fields. However, these approaches may not work for the autonomous multi-robot optical inspection system due to fast computation requirements of inline optimization, unique characteristics on robotic end-effector orientations, and complex large-scale free-form product surfaces. This paper proposes a novel task allocation methodology for coordinated motion planning of multi-robot inspection. Specifically, (1) a local robust inspection task allocation is proposed to achieve efficient and well-balanced measurement assignment among robots; (2) collision-free path planning and coordinated motion planning are developed via dynamic searching in robotic coordinate space and perturbation of probe poses or local paths in the conflicting robots. A case study shows that the proposed approach can mitigate the risk of collisions between robots and environments, resolve conflicts among robots, and reduce the inspection cycle time significantly and consistently.

Partitioned Active Learning for Heterogeneous Systems

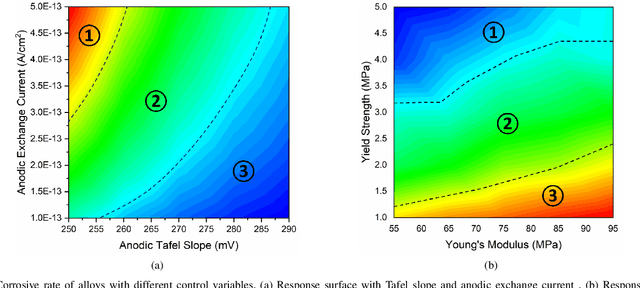
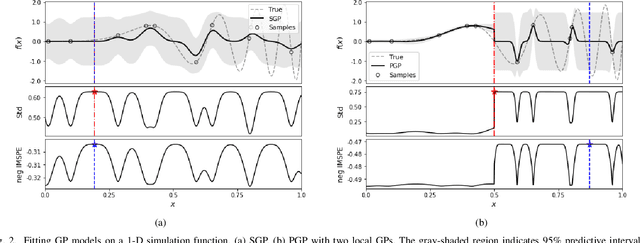
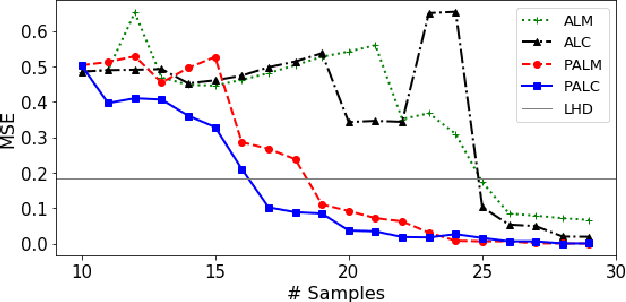
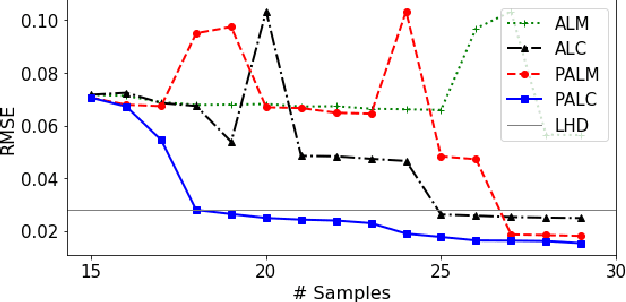
Cost-effective and high-precision surrogate modeling is a cornerstone of automated industrial and engineering systems. Active learning coupled with Gaussian process (GP) surrogate modeling is an indispensable tool for demanding and complex systems, while the existence of heterogeneity in underlying systems may adversely affect the modeling process. In order to improve the learning efficiency under the regime, we propose the partitioned active learning strategy established upon partitioned GP (PGP) modeling. Our strategy seeks the most informative design point for PGP modeling systematically in twosteps. The global searching scheme accelerates the exploration aspect of active learning by investigating the most uncertain design space, and the local searching exploits the active learning criterion induced by the local GP model. We also provide numerical remedies to alleviate the computational cost of active learning, thereby allowing the proposed method to incorporate a large amount of candidates. The proposed method is applied to numerical simulation and real world cases endowed with heterogeneities in which surrogate models are constructed to embed in (i) the cost-efficient automatic fuselage shape control system; and (ii) the optimal design system of tribocorrosion-resistant alloys. The results show that our approach outperforms benchmark methods.