A Cycle GAN Approach for Heterogeneous Domain Adaptation in Land Use Classification

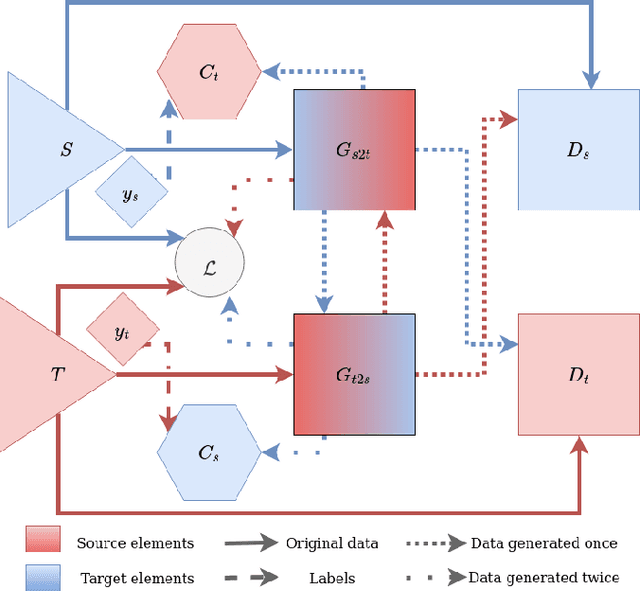
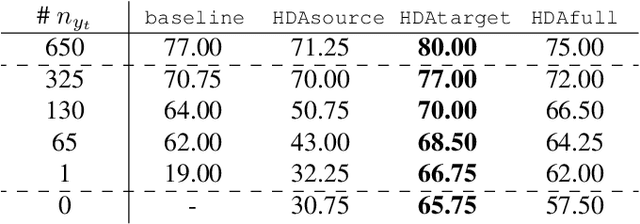
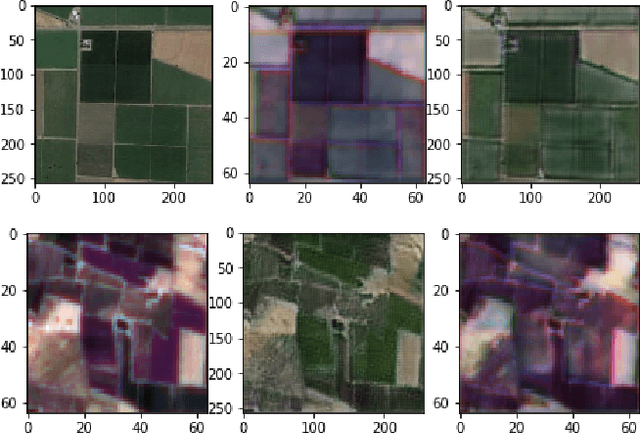
In the field of remote sensing and more specifically in Earth Observation, new data are available every day, coming from different sensors. Leveraging on those data in classification tasks comes at the price of intense labelling tasks that are not realistic in operational settings. While domain adaptation could be useful to counterbalance this problem, most of the usual methods assume that the data to adapt are comparable (they belong to the same metric space), which is not the case when multiple sensors are at stake. Heterogeneous domain adaptation methods are a particular solution to this problem. We present a novel method to deal with such cases, based on a modified cycleGAN version that incorporates classification losses and a metric space alignment term. We demonstrate its power on a land use classification tasks, with images from both Google Earth and Sentinel-2.

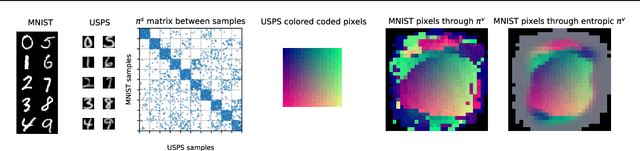
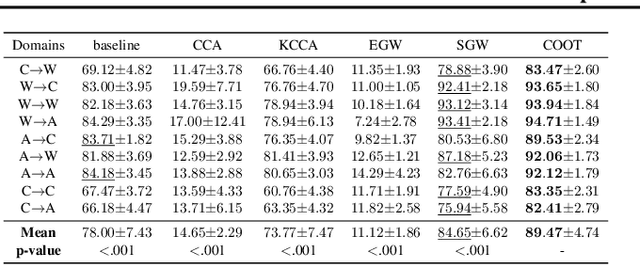
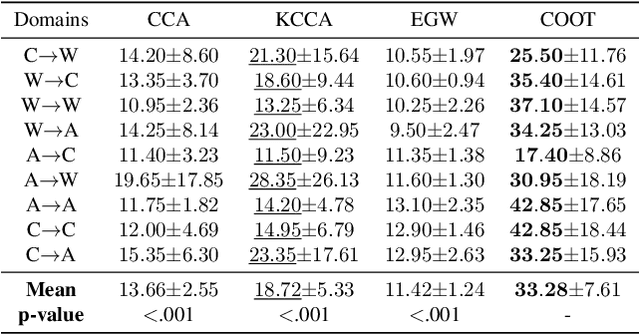
CO-Optimal Transport

Optimal transport (OT) is a powerful geometric and probabilistic tool for finding correspondences and measuring similarity between two distributions. Yet, its original formulation relies on the existence of a cost function between the samples of the two distributions, which makes it impractical for comparing data distributions supported on different topological spaces. To circumvent this limitation, we propose a novel OT problem, named COOT for CO-Optimal Transport, that aims to simultaneously optimize two transport maps between both samples and features. This is different from other approaches that either discard the individual features by focussing on pairwise distances (e.g. Gromov-Wasserstein) or need to model explicitly the relations between the features. COOT leads to interpretable correspondences between both samples and feature representations and holds metric properties. We provide a thorough theoretical analysis of our framework and establish rich connections with the Gromov-Wasserstein distance. We demonstrate its versatility with two machine learning applications in heterogeneous domain adaptation and co-clustering/data summarization, where COOT leads to performance improvements over the competing state-of-the-art methods.

Time Series Alignment with Global Invariances

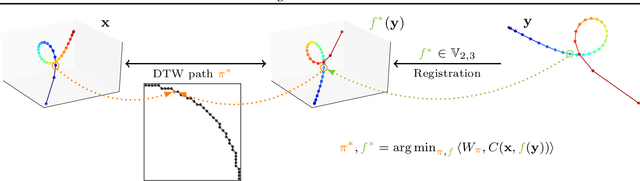
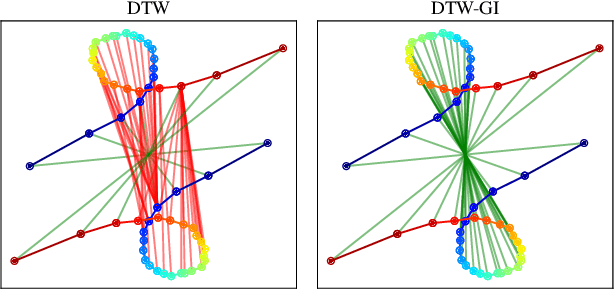
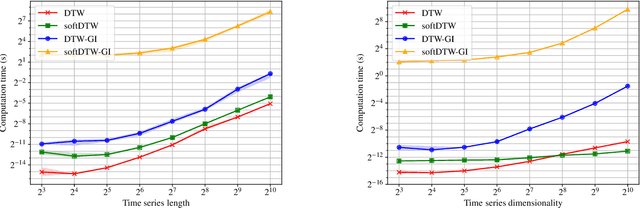
In this work we address the problem of comparing time series while taking into account both feature space transformation and temporal variability. The proposed framework combines a latent global transformation of the feature space with the widely used Dynamic Time Warping (DTW). The latent global transformation captures the feature invariance while the DTW (or its smooth counterpart soft-DTW) deals with the temporal shifts. We cast the problem as a joint optimization over the global transformation and the temporal alignments. The versatility of our framework allows for several variants depending on the invariance class at stake. Among our contributions we define a differentiable loss for time series and present two algorithms for the computation of time series barycenters under our new geometry. We illustrate the interest of our approach on both simulated and real world data.

Generating Natural Adversarial Hyperspectral examples with a modified Wasserstein GAN

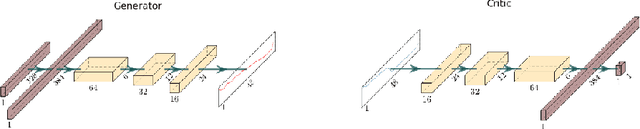
Adversarial examples are a hot topic due to their abilities to fool a classifier's prediction. There are two strategies to create such examples, one uses the attacked classifier's gradients, while the other only requires access to the clas-sifier's prediction. This is particularly appealing when the classifier is not full known (black box model). In this paper, we present a new method which is able to generate natural adversarial examples from the true data following the second paradigm. Based on Generative Adversarial Networks (GANs) [5], it reweights the true data empirical distribution to encourage the classifier to generate ad-versarial examples. We provide a proof of concept of our method by generating adversarial hyperspectral signatures on a remote sensing dataset.

Learning with minibatch Wasserstein : asymptotic and gradient properties

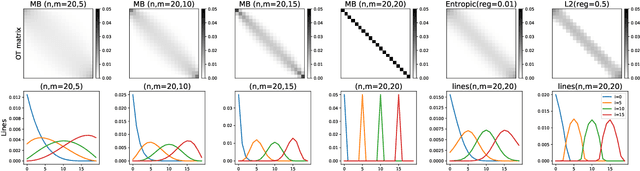
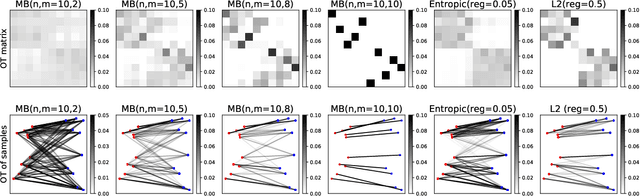
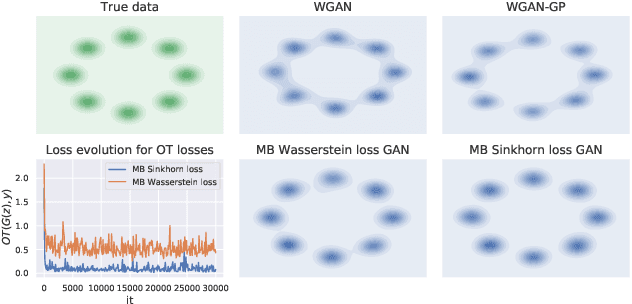
Optimal transport distances are powerful tools to compare probability distributions and have found many applications in machine learning. Yet their algorithmic complexity prevents their direct use on large scale datasets. To overcome this challenge, practitioners compute these distances on minibatches {\em i.e.} they average the outcome of several smaller optimal transport problems. We propose in this paper an analysis of this practice, which effects are not well understood so far. We notably argue that it is equivalent to an implicit regularization of the original problem, with appealing properties such as unbiased estimators, gradients and a concentration bound around the expectation, but also with defects such as loss of distance property. Along with this theoretical analysis, we also conduct empirical experiments on gradient flows, GANs or color transfer that highlight the practical interest of this strategy.

Sliced Gromov-Wasserstein

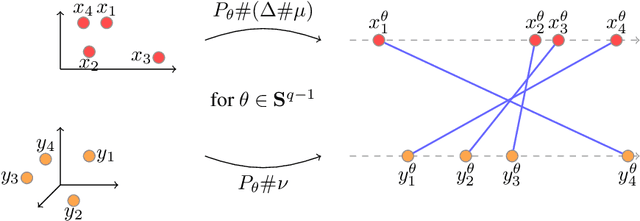
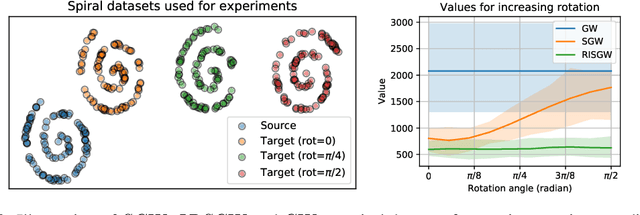
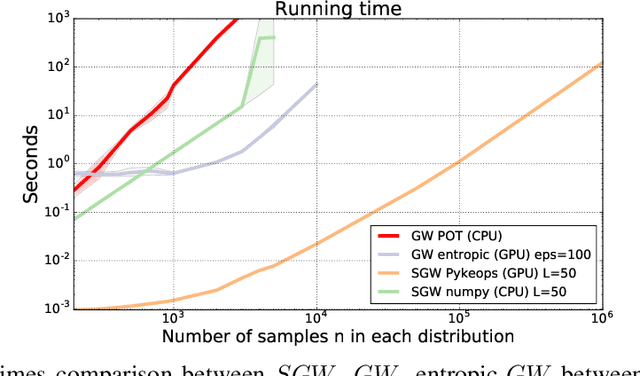
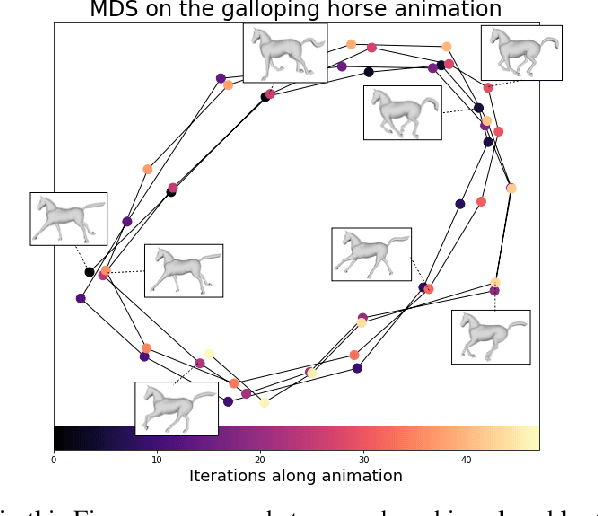
Recently used in various machine learning contexts, the Gromov-Wasserstein distance (GW) allows for comparing distributions that do not necessarily lie in the same metric space. However, this Optimal Transport (OT) distance requires solving a complex non convex quadratic program which is most of the time very costly both in time and memory. Contrary to GW, the Wasserstein distance (W) enjoys several properties (e.g. duality) that permit large scale optimization. Among those, the Sliced Wasserstein (SW) distance exploits the direct solution of W on the line, that only requires sorting discrete samples in 1D. This paper propose a new divergence based on GW akin to SW. We first derive a closed form for GW when dealing with 1D distributions, based on a new result for the related quadratic assignment problem. We then define a novel OT discrepancy that can deal with large scale distributions via a slicing approach and we show how it relates to the GW distance while being $O(n^2)$ to compute. We illustrate the behavior of this so called Sliced Gromov-Wasserstein (SGW) discrepancy in experiments where we demonstrate its ability to tackle similar problems as GW while being several order of magnitudes faster to compute

Pushing the right boundaries matters! Wasserstein Adversarial Training for Label Noise

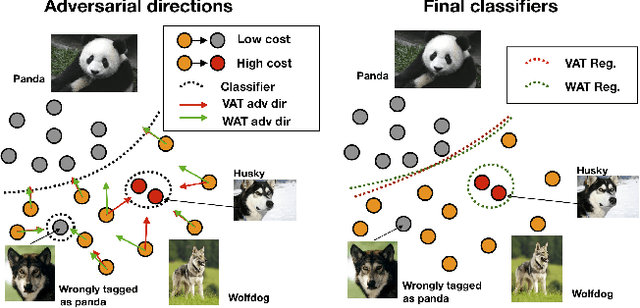
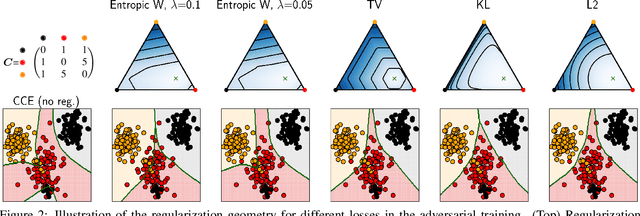
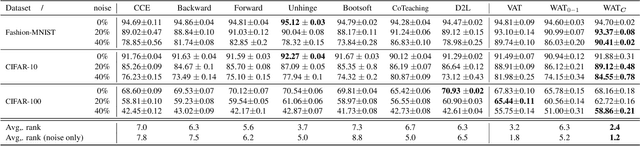
Noisy labels often occur in vision datasets, especially when they are issued from crowdsourcing or Web scraping. In this paper, we propose a new regularization method which enables one to learn robust classifiers in presence of noisy data. To achieve this goal, we augment the virtual adversarial loss with a Wasserstein distance. This distance allows us to take into account specific relations between classes by leveraging on the geometric properties of this optimal transport distance. Notably, we encode the class similarities in the ground cost that is used to compute the Wasserstein distance. As a consequence, we can promote smoothness between classes that are very dissimilar, while keeping the classification decision function sufficiently complex for similar classes. While designing this ground cost can be left as a problem-specific modeling task, we show in this paper that using the semantic relations between classes names already leads to good results.Our proposed Wasserstein Adversarial Training (WAT) outperforms state of the art on four datasets corrupted with noisy labels: three classical benchmarks and one real case in remote sensing image semantic segmentation.

End-to-end Learning for Early Classification of Time Series

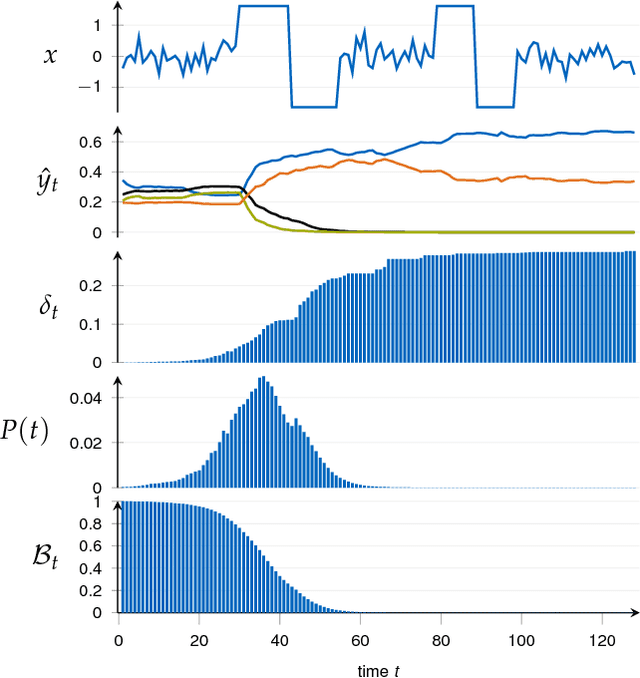
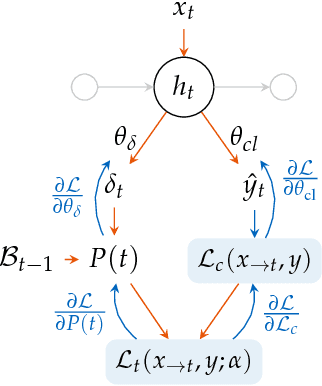
Classification of time series is a topical issue in machine learning. While accuracy stands for the most important evaluation criterion, some applications require decisions to be made as early as possible. Optimization should then target a compromise between earliness, i.e., a capacity of providing a decision early in the sequence, and accuracy. In this work, we propose a generic, end-to-end trainable framework for early classification of time series. This framework embeds a learnable decision mechanism that can be plugged into a wide range of already existing models. We present results obtained with deep neural networks on a diverse set of time series classification problems. Our approach compares well to state-of-the-art competitors while being easily adaptable by any existing neural network topology that evaluates a hidden state at each time step.

Fused Gromov-Wasserstein distance for structured objects: theoretical foundations and mathematical properties

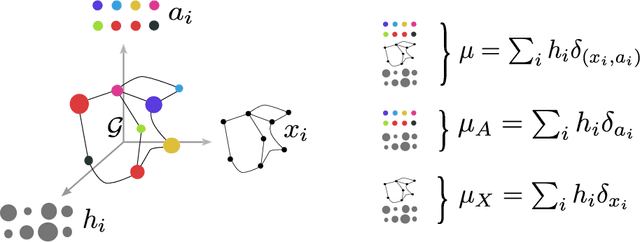
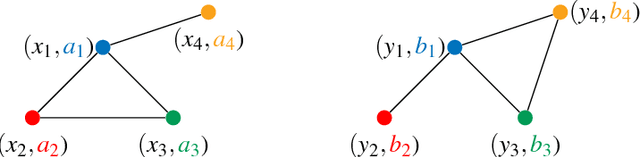
Optimal transport theory has recently found many applications in machine learning thanks to its capacity for comparing various machine learning objects considered as distributions. The Kantorovitch formulation, leading to the Wasserstein distance, focuses on the features of the elements of the objects but treat them independently, whereas the Gromov-Wasserstein distance focuses only on the relations between the elements, depicting the structure of the object, yet discarding its features. In this paper we propose to extend these distances in order to encode simultaneously both the feature and structure informations, resulting in the Fused Gromov-Wasserstein distance. We develop the mathematical framework for this novel distance, prove its metric and interpolation properties and provide a concentration result for the convergence of finite samples. We also illustrate and interpret its use in various contexts where structured objects are involved.

An Entropic Optimal Transport Loss for Learning Deep Neural Networks under Label Noise in Remote Sensing Images

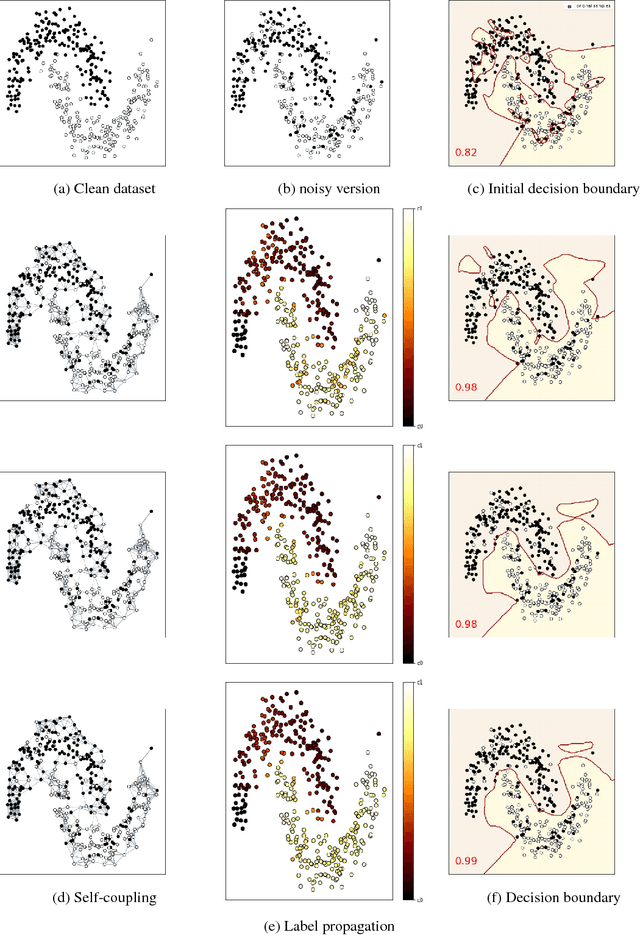
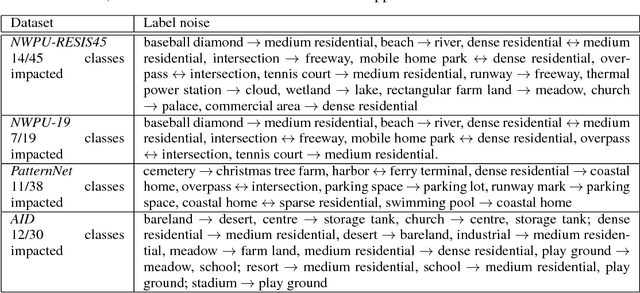
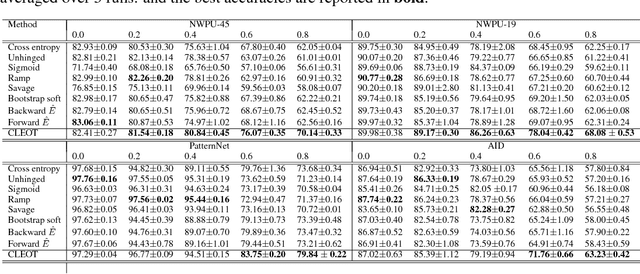
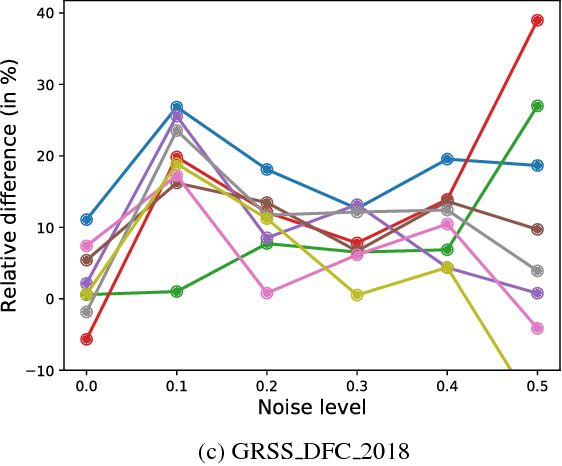
Deep neural networks have established as a powerful tool for large scale supervised classification tasks. The state-of-the-art performances of deep neural networks are conditioned to the availability of large number of accurately labeled samples. In practice, collecting large scale accurately labeled datasets is a challenging and tedious task in most scenarios of remote sensing image analysis, thus cheap surrogate procedures are employed to label the dataset. Training deep neural networks on such datasets with inaccurate labels easily overfits to the noisy training labels and degrades the performance of the classification tasks drastically. To mitigate this effect, we propose an original solution with entropic optimal transportation. It allows to learn in an end-to-end fashion deep neural networks that are, to some extent, robust to inaccurately labeled samples. We empirically demonstrate on several remote sensing datasets, where both scene and pixel-based hyperspectral images are considered for classification. Our method proves to be highly tolerant to significant amounts of label noise and achieves favorable results against state-of-the-art methods.