When Actions Teach You to Think: Reasoning-Action Synergy via Reinforcement Learning in Conversational Agents

Supervised fine-tuning (SFT) has emerged as one of the most effective ways to improve the performance of large language models (LLMs) in downstream tasks. However, SFT can have difficulty generalizing when the underlying data distribution changes, even when the new data does not fall completely outside the training domain. Recent reasoning-focused models such as o1 and R1 have demonstrated consistent gains over their non-reasoning counterparts, highlighting the importance of reasoning for improved generalization and reliability. However, collecting high-quality reasoning traces for SFT remains challenging -- annotations are costly, subjective, and difficult to scale. To address this limitation, we leverage Reinforcement Learning (RL) to enable models to learn reasoning strategies directly from task outcomes. We propose a pipeline in which LLMs generate reasoning steps that guide both the invocation of tools (e.g., function calls) and the final answer generation for conversational agents. Our method employs Group Relative Policy Optimization (GRPO) with rewards designed around tool accuracy and answer correctness, allowing the model to iteratively refine its reasoning and actions. Experimental results demonstrate that our approach improves both the quality of reasoning and the precision of tool invocations, achieving a 1.5% relative improvement over the SFT model (trained without explicit thinking) and a 40% gain compared to the base of the vanilla Qwen3-1.7B model. These findings demonstrate the promise of unifying reasoning and action learning through RL to build more capable and generalizable conversational agents.

DySK-Attn: A Framework for Efficient, Real-Time Knowledge Updating in Large Language Models via Dynamic Sparse Knowledge Attention

Large Language Models (LLMs) suffer from a critical limitation: their knowledge is static and quickly becomes outdated. Retraining these massive models is computationally prohibitive, while existing knowledge editing techniques can be slow and may introduce unforeseen side effects. To address this, we propose DySK-Attn, a novel framework that enables LLMs to efficiently integrate real-time knowledge from a dynamic external source. Our approach synergizes an LLM with a dynamic Knowledge Graph (KG) that can be updated instantaneously. The core of our framework is a sparse knowledge attention mechanism, which allows the LLM to perform a coarse-to-fine grained search, efficiently identifying and focusing on a small, highly relevant subset of facts from the vast KG. This mechanism avoids the high computational cost of dense attention over the entire knowledge base and mitigates noise from irrelevant information. We demonstrate through extensive experiments on time-sensitive question-answering tasks that DySK-Attn significantly outperforms strong baselines, including standard Retrieval-Augmented Generation (RAG) and model editing techniques, in both factual accuracy for updated knowledge and computational efficiency. Our framework offers a scalable and effective solution for building LLMs that can stay current with the ever-changing world.

Voxtral

We present Voxtral Mini and Voxtral Small, two multimodal audio chat models. Voxtral is trained to comprehend both spoken audio and text documents, achieving state-of-the-art performance across a diverse range of audio benchmarks, while preserving strong text capabilities. Voxtral Small outperforms a number of closed-source models, while being small enough to run locally. A 32K context window enables the model to handle audio files up to 40 minutes in duration and long multi-turn conversations. We also contribute three benchmarks for evaluating speech understanding models on knowledge and trivia. Both Voxtral models are released under Apache 2.0 license.

Magistral

We introduce Magistral, Mistral's first reasoning model and our own scalable reinforcement learning (RL) pipeline. Instead of relying on existing implementations and RL traces distilled from prior models, we follow a ground up approach, relying solely on our own models and infrastructure. Notably, we demonstrate a stack that enabled us to explore the limits of pure RL training of LLMs, present a simple method to force the reasoning language of the model, and show that RL on text data alone maintains most of the initial checkpoint's capabilities. We find that RL on text maintains or improves multimodal understanding, instruction following and function calling. We present Magistral Medium, trained for reasoning on top of Mistral Medium 3 with RL alone, and we open-source Magistral Small (Apache 2.0) which further includes cold-start data from Magistral Medium.

Pre-Act: Multi-Step Planning and Reasoning Improves Acting in LLM Agents

The ReAct (Reasoning + Action) capability in large language models (LLMs) has become the foundation of modern agentic systems. Recent LLMs, such as DeepSeek-R1 and OpenAI o1/o3, exemplify this by emphasizing reasoning through the generation of ample intermediate tokens, which help build a strong premise before producing the final output tokens. In this paper, we introduce Pre-Act, a novel approach that enhances the agent's performance by creating a multi-step execution plan along with the detailed reasoning for the given user input. This plan incrementally incorporates previous steps and tool outputs, refining itself after each step execution until the final response is obtained. Our approach is applicable to both conversational and non-conversational agents. To measure the performance of task-oriented agents comprehensively, we propose a two-level evaluation framework: (1) turn level and (2) end-to-end. Our turn-level evaluation, averaged across five models, shows that our approach, Pre-Act, outperforms ReAct by 70% in Action Recall on the Almita dataset. While this approach is effective for larger models, smaller models crucial for practical applications, where latency and cost are key constraints, often struggle with complex reasoning tasks required for agentic systems. To address this limitation, we fine-tune relatively small models such as Llama 3.1 (8B & 70B) using the proposed Pre-Act approach. Our experiments show that the fine-tuned 70B model outperforms GPT-4, achieving a 69.5% improvement in action accuracy (turn-level) and a 28% improvement in goal completion rate (end-to-end) on the Almita (out-of-domain) dataset.

Faster Cascades via Speculative Decoding

Cascades and speculative decoding are two common approaches to improving language models' inference efficiency. Both approaches involve interleaving models of different sizes, but via fundamentally distinct mechanisms: cascades employ a deferral rule that invokes the larger model only for "hard" inputs, while speculative decoding uses speculative execution to primarily invoke the larger model in parallel verification mode. These mechanisms offer different benefits: empirically, cascades are often capable of yielding better quality than even the larger model, while theoretically, speculative decoding offers a guarantee of quality-neutrality. In this paper, we leverage the best of both these approaches by designing new speculative cascading techniques that implement their deferral rule through speculative execution. We characterize the optimal deferral rule for our speculative cascades, and employ a plug-in approximation to the optimal rule. Through experiments with T5 models on benchmark language tasks, we show that the proposed approach yields better cost-quality trade-offs than cascading and speculative decoding baselines.

Language Model Cascades: Token-level uncertainty and beyond

Recent advances in language models (LMs) have led to significant improvements in quality on complex NLP tasks, but at the expense of increased inference costs. Cascading offers a simple strategy to achieve more favorable cost-quality tradeoffs: here, a small model is invoked for most "easy" instances, while a few "hard" instances are deferred to the large model. While the principles underpinning cascading are well-studied for classification tasks - with deferral based on predicted class uncertainty favored theoretically and practically - a similar understanding is lacking for generative LM tasks. In this work, we initiate a systematic study of deferral rules for LM cascades. We begin by examining the natural extension of predicted class uncertainty to generative LM tasks, namely, the predicted sequence uncertainty. We show that this measure suffers from the length bias problem, either over- or under-emphasizing outputs based on their lengths. This is because LMs produce a sequence of uncertainty values, one for each output token; and moreover, the number of output tokens is variable across examples. To mitigate this issue, we propose to exploit the richer token-level uncertainty information implicit in generative LMs. We argue that naive predicted sequence uncertainty corresponds to a simple aggregation of these uncertainties. By contrast, we show that incorporating token-level uncertainty through learned post-hoc deferral rules can significantly outperform such simple aggregation strategies, via experiments on a range of natural language benchmarks with FLAN-T5 models. We further show that incorporating embeddings from the smaller model and intermediate layers of the larger model can give an additional boost in the overall cost-quality tradeoff.

When Does Confidence-Based Cascade Deferral Suffice?

Cascades are a classical strategy to enable inference cost to vary adaptively across samples, wherein a sequence of classifiers are invoked in turn. A deferral rule determines whether to invoke the next classifier in the sequence, or to terminate prediction. One simple deferral rule employs the confidence of the current classifier, e.g., based on the maximum predicted softmax probability. Despite being oblivious to the structure of the cascade -- e.g., not modelling the errors of downstream models -- such confidence-based deferral often works remarkably well in practice. In this paper, we seek to better understand the conditions under which confidence-based deferral may fail, and when alternate deferral strategies can perform better. We first present a theoretical characterisation of the optimal deferral rule, which precisely characterises settings under which confidence-based deferral may suffer. We then study post-hoc deferral mechanisms, and demonstrate they can significantly improve upon confidence-based deferral in settings where (i) downstream models are specialists that only work well on a subset of inputs, (ii) samples are subject to label noise, and (iii) there is distribution shift between the train and test set.

Ensembling over Classifiers: a Bias-Variance Perspective

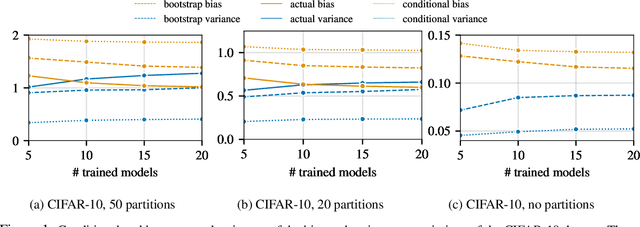
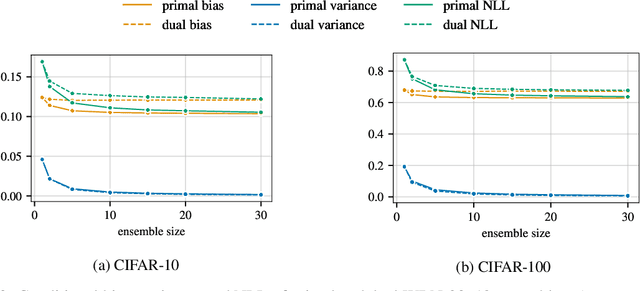
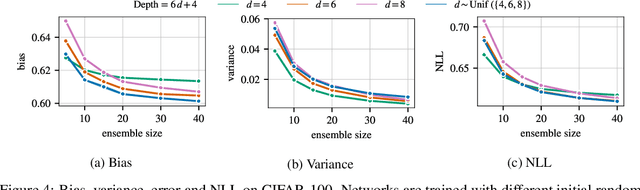
Ensembles are a straightforward, remarkably effective method for improving the accuracy,calibration, and robustness of models on classification tasks; yet, the reasons that underlie their success remain an active area of research. We build upon the extension to the bias-variance decomposition by Pfau (2013) in order to gain crucial insights into the behavior of ensembles of classifiers. Introducing a dual reparameterization of the bias-variance tradeoff, we first derive generalized laws of total expectation and variance for nonsymmetric losses typical of classification tasks. Comparing conditional and bootstrap bias/variance estimates, we then show that conditional estimates necessarily incur an irreducible error. Next, we show that ensembling in dual space reduces the variance and leaves the bias unchanged, whereas standard ensembling can arbitrarily affect the bias. Empirically, standard ensembling reducesthe bias, leading us to hypothesize that ensembles of classifiers may perform well in part because of this unexpected reduction.We conclude by an empirical analysis of recent deep learning methods that ensemble over hyperparameters, revealing that these techniques indeed favor bias reduction. This suggests that, contrary to classical wisdom, targeting bias reduction may be a promising direction for classifier ensembles.

Understanding the bias-variance tradeoff of Bregman divergences

This paper builds upon the work of Pfau (2013), which generalized the bias variance tradeoff to any Bregman divergence loss function. Pfau (2013) showed that for Bregman divergences, the bias and variances are defined with respect to a central label, defined as the mean of the label variable, and a central prediction, of a more complex form. We show that, similarly to the label, the central prediction can be interpreted as the mean of a random variable, where the mean operates in a dual space defined by the loss function itself. Viewing the bias-variance tradeoff through operations taken in dual space, we subsequently derive several results of interest. In particular, (a) the variance terms satisfy a generalized law of total variance; (b) if a source of randomness cannot be controlled, its contribution to the bias and variance has a closed form; (c) there exist natural ensembling operations in the label and prediction spaces which reduce the variance and do not affect the bias.