Predicting quantum channels over general product distributions

We investigate the problem of predicting the output behavior of unknown quantum channels. Given query access to an $n$-qubit channel $E$ and an observable $O$, we aim to learn the mapping \begin{equation*} \rho \mapsto \mathrm{Tr}(O E[\rho]) \end{equation*} to within a small error for most $\rho$ sampled from a distribution $D$. Previously, Huang, Chen, and Preskill proved a surprising result that even if $E$ is arbitrary, this task can be solved in time roughly $n^{O(\log(1/\epsilon))}$, where $\epsilon$ is the target prediction error. However, their guarantee applied only to input distributions $D$ invariant under all single-qubit Clifford gates, and their algorithm fails for important cases such as general product distributions over product states $\rho$. In this work, we propose a new approach that achieves accurate prediction over essentially any product distribution $D$, provided it is not "classical" in which case there is a trivial exponential lower bound. Our method employs a "biased Pauli analysis," analogous to classical biased Fourier analysis. Implementing this approach requires overcoming several challenges unique to the quantum setting, including the lack of a basis with appropriate orthogonality properties. The techniques we develop to address these issues may have broader applications in quantum information.

Harnessing the Power of Choices in Decision Tree Learning

We propose a simple generalization of standard and empirically successful decision tree learning algorithms such as ID3, C4.5, and CART. These algorithms, which have been central to machine learning for decades, are greedy in nature: they grow a decision tree by iteratively splitting on the best attribute. Our algorithm, Top-$k$, considers the $k$ best attributes as possible splits instead of just the single best attribute. We demonstrate, theoretically and empirically, the power of this simple generalization. We first prove a {\sl greediness hierarchy theorem} showing that for every $k \in \mathbb{N}$, Top-$(k+1)$ can be dramatically more powerful than Top-$k$: there are data distributions for which the former achieves accuracy $1-\varepsilon$, whereas the latter only achieves accuracy $\frac1{2}+\varepsilon$. We then show, through extensive experiments, that Top-$k$ outperforms the two main approaches to decision tree learning: classic greedy algorithms and more recent "optimal decision tree" algorithms. On one hand, Top-$k$ consistently enjoys significant accuracy gains over greedy algorithms across a wide range of benchmarks. On the other hand, Top-$k$ is markedly more scalable than optimal decision tree algorithms and is able to handle dataset and feature set sizes that remain far beyond the reach of these algorithms.

Agnostic proper learning of monotone functions: beyond the black-box correction barrier

We give the first agnostic, efficient, proper learning algorithm for monotone Boolean functions. Given $2^{\tilde{O}(\sqrt{n}/\varepsilon)}$ uniformly random examples of an unknown function $f:\{\pm 1\}^n \rightarrow \{\pm 1\}$, our algorithm outputs a hypothesis $g:\{\pm 1\}^n \rightarrow \{\pm 1\}$ that is monotone and $(\mathrm{opt} + \varepsilon)$-close to $f$, where $\mathrm{opt}$ is the distance from $f$ to the closest monotone function. The running time of the algorithm (and consequently the size and evaluation time of the hypothesis) is also $2^{\tilde{O}(\sqrt{n}/\varepsilon)}$, nearly matching the lower bound of Blais et al (RANDOM '15). We also give an algorithm for estimating up to additive error $\varepsilon$ the distance of an unknown function $f$ to monotone using a run-time of $2^{\tilde{O}(\sqrt{n}/\varepsilon)}$. Previously, for both of these problems, sample-efficient algorithms were known, but these algorithms were not run-time efficient. Our work thus closes this gap in our knowledge between the run-time and sample complexity. This work builds upon the improper learning algorithm of Bshouty and Tamon (JACM '96) and the proper semiagnostic learning algorithm of Lange, Rubinfeld, and Vasilyan (FOCS '22), which obtains a non-monotone Boolean-valued hypothesis, then ``corrects'' it to monotone using query-efficient local computation algorithms on graphs. This black-box correction approach can achieve no error better than $2\mathrm{opt} + \varepsilon$ information-theoretically; we bypass this barrier by a) augmenting the improper learner with a convex optimization step, and b) learning and correcting a real-valued function before rounding its values to Boolean. Our real-valued correction algorithm solves the ``poset sorting'' problem of [LRV22] for functions over general posets with non-Boolean labels.

Lifting uniform learners via distributional decomposition

We show how any PAC learning algorithm that works under the uniform distribution can be transformed, in a blackbox fashion, into one that works under an arbitrary and unknown distribution $\mathcal{D}$. The efficiency of our transformation scales with the inherent complexity of $\mathcal{D}$, running in $\mathrm{poly}(n, (md)^d)$ time for distributions over $\{\pm 1\}^n$ whose pmfs are computed by depth-$d$ decision trees, where $m$ is the sample complexity of the original algorithm. For monotone distributions our transformation uses only samples from $\mathcal{D}$, and for general ones it uses subcube conditioning samples. A key technical ingredient is an algorithm which, given the aforementioned access to $\mathcal{D}$, produces an optimal decision tree decomposition of $\mathcal{D}$: an approximation of $\mathcal{D}$ as a mixture of uniform distributions over disjoint subcubes. With this decomposition in hand, we run the uniform-distribution learner on each subcube and combine the hypotheses using the decision tree. This algorithmic decomposition lemma also yields new algorithms for learning decision tree distributions with runtimes that exponentially improve on the prior state of the art -- results of independent interest in distribution learning.

A Query-Optimal Algorithm for Finding Counterfactuals

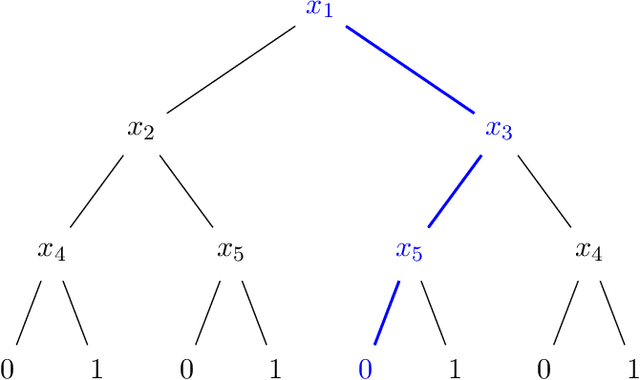
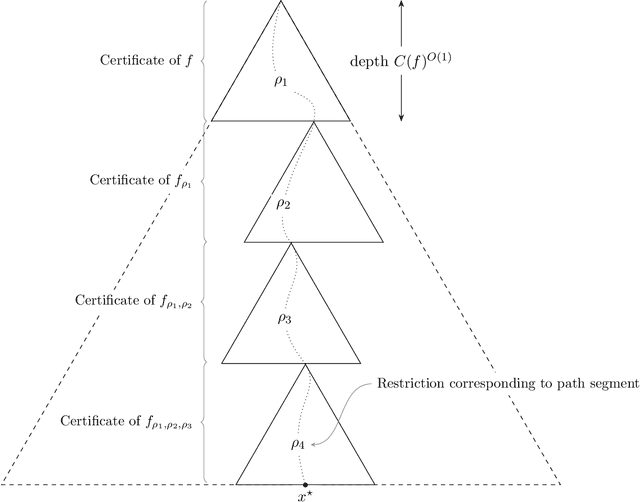
We design an algorithm for finding counterfactuals with strong theoretical guarantees on its performance. For any monotone model $f : X^d \to \{0,1\}$ and instance $x^\star$, our algorithm makes \[ {S(f)^{O(\Delta_f(x^\star))}\cdot \log d}\] queries to $f$ and returns {an {\sl optimal}} counterfactual for $x^\star$: a nearest instance $x'$ to $x^\star$ for which $f(x')\ne f(x^\star)$. Here $S(f)$ is the sensitivity of $f$, a discrete analogue of the Lipschitz constant, and $\Delta_f(x^\star)$ is the distance from $x^\star$ to its nearest counterfactuals. The previous best known query complexity was $d^{\,O(\Delta_f(x^\star))}$, achievable by brute-force local search. We further prove a lower bound of $S(f)^{\Omega(\Delta_f(x^\star))} + \Omega(\log d)$ on the query complexity of any algorithm, thereby showing that the guarantees of our algorithm are essentially optimal.

Open Problem: Properly learning decision trees in polynomial time?

The authors recently gave an $n^{O(\log\log n)}$ time membership query algorithm for properly learning decision trees under the uniform distribution (Blanc et al., 2021). The previous fastest algorithm for this problem ran in $n^{O(\log n)}$ time, a consequence of Ehrenfeucht and Haussler (1989)'s classic algorithm for the distribution-free setting. In this article we highlight the natural open problem of obtaining a polynomial-time algorithm, discuss possible avenues towards obtaining it, and state intermediate milestones that we believe are of independent interest.

Popular decision tree algorithms are provably noise tolerant

Using the framework of boosting, we prove that all impurity-based decision tree learning algorithms, including the classic ID3, C4.5, and CART, are highly noise tolerant. Our guarantees hold under the strongest noise model of nasty noise, and we provide near-matching upper and lower bounds on the allowable noise rate. We further show that these algorithms, which are simple and have long been central to everyday machine learning, enjoy provable guarantees in the noisy setting that are unmatched by existing algorithms in the theoretical literature on decision tree learning. Taken together, our results add to an ongoing line of research that seeks to place the empirical success of these practical decision tree algorithms on firm theoretical footing.

On the power of adaptivity in statistical adversaries

We study a fundamental question concerning adversarial noise models in statistical problems where the algorithm receives i.i.d. draws from a distribution $\mathcal{D}$. The definitions of these adversaries specify the type of allowable corruptions (noise model) as well as when these corruptions can be made (adaptivity); the latter differentiates between oblivious adversaries that can only corrupt the distribution $\mathcal{D}$ and adaptive adversaries that can have their corruptions depend on the specific sample $S$ that is drawn from $\mathcal{D}$. In this work, we investigate whether oblivious adversaries are effectively equivalent to adaptive adversaries, across all noise models studied in the literature. Specifically, can the behavior of an algorithm $\mathcal{A}$ in the presence of oblivious adversaries always be well-approximated by that of an algorithm $\mathcal{A}'$ in the presence of adaptive adversaries? Our first result shows that this is indeed the case for the broad class of statistical query algorithms, under all reasonable noise models. We then show that in the specific case of additive noise, this equivalence holds for all algorithms. Finally, we map out an approach towards proving this statement in its fullest generality, for all algorithms and under all reasonable noise models.

Provably efficient, succinct, and precise explanations

We consider the problem of explaining the predictions of an arbitrary blackbox model $f$: given query access to $f$ and an instance $x$, output a small set of $x$'s features that in conjunction essentially determines $f(x)$. We design an efficient algorithm with provable guarantees on the succinctness and precision of the explanations that it returns. Prior algorithms were either efficient but lacked such guarantees, or achieved such guarantees but were inefficient. We obtain our algorithm via a connection to the problem of {\sl implicitly} learning decision trees. The implicit nature of this learning task allows for efficient algorithms even when the complexity of $f$ necessitates an intractably large surrogate decision tree. We solve the implicit learning problem by bringing together techniques from learning theory, local computation algorithms, and complexity theory. Our approach of "explaining by implicit learning" shares elements of two previously disparate methods for post-hoc explanations, global and local explanations, and we make the case that it enjoys advantages of both.

Properly learning decision trees in almost polynomial time

We give an $n^{O(\log\log n)}$-time membership query algorithm for properly and agnostically learning decision trees under the uniform distribution over $\{\pm 1\}^n$. Even in the realizable setting, the previous fastest runtime was $n^{O(\log n)}$, a consequence of a classic algorithm of Ehrenfeucht and Haussler. Our algorithm shares similarities with practical heuristics for learning decision trees, which we augment with additional ideas to circumvent known lower bounds against these heuristics. To analyze our algorithm, we prove a new structural result for decision trees that strengthens a theorem of O'Donnell, Saks, Schramm, and Servedio. While the OSSS theorem says that every decision tree has an influential variable, we show how every decision tree can be "pruned" so that every variable in the resulting tree is influential.