Computational-Statistical Tradeoffs from NP-hardness

A central question in computer science and statistics is whether efficient algorithms can achieve the information-theoretic limits of statistical problems. Many computational-statistical tradeoffs have been shown under average-case assumptions, but since statistical problems are average-case in nature, it has been a challenge to base them on standard worst-case assumptions. In PAC learning where such tradeoffs were first studied, the question is whether computational efficiency can come at the cost of using more samples than information-theoretically necessary. We base such tradeoffs on $\mathsf{NP}$-hardness and obtain: $\circ$ Sharp computational-statistical tradeoffs assuming $\mathsf{NP}$ requires exponential time: For every polynomial $p(n)$, there is an $n$-variate class $C$ with VC dimension $1$ such that the sample complexity of time-efficiently learning $C$ is $\Theta(p(n))$. $\circ$ A characterization of $\mathsf{RP}$ vs. $\mathsf{NP}$ in terms of learning: $\mathsf{RP} = \mathsf{NP}$ iff every $\mathsf{NP}$-enumerable class is learnable with $O(\mathrm{VCdim}(C))$ samples in polynomial time. The forward implication has been known since (Pitt and Valiant, 1988); we prove the reverse implication. Notably, all our lower bounds hold against improper learners. These are the first $\mathsf{NP}$-hardness results for improperly learning a subclass of polynomial-size circuits, circumventing formal barriers of Applebaum, Barak, and Xiao (2008).

The Sample Complexity of Smooth Boosting and the Tightness of the Hardcore Theorem

Smooth boosters generate distributions that do not place too much weight on any given example. Originally introduced for their noise-tolerant properties, such boosters have also found applications in differential privacy, reproducibility, and quantum learning theory. We study and settle the sample complexity of smooth boosting: we exhibit a class that can be weak learned to $\gamma$-advantage over smooth distributions with $m$ samples, for which strong learning over the uniform distribution requires $\tilde{\Omega}(1/\gamma^2)\cdot m$ samples. This matches the overhead of existing smooth boosters and provides the first separation from the setting of distribution-independent boosting, for which the corresponding overhead is $O(1/\gamma)$. Our work also sheds new light on Impagliazzo's hardcore theorem from complexity theory, all known proofs of which can be cast in the framework of smooth boosting. For a function $f$ that is mildly hard against size-$s$ circuits, the hardcore theorem provides a set of inputs on which $f$ is extremely hard against size-$s'$ circuits. A downside of this important result is the loss in circuit size, i.e. that $s' \ll s$. Answering a question of Trevisan, we show that this size loss is necessary and in fact, the parameters achieved by known proofs are the best possible.

Superconstant Inapproximability of Decision Tree Learning

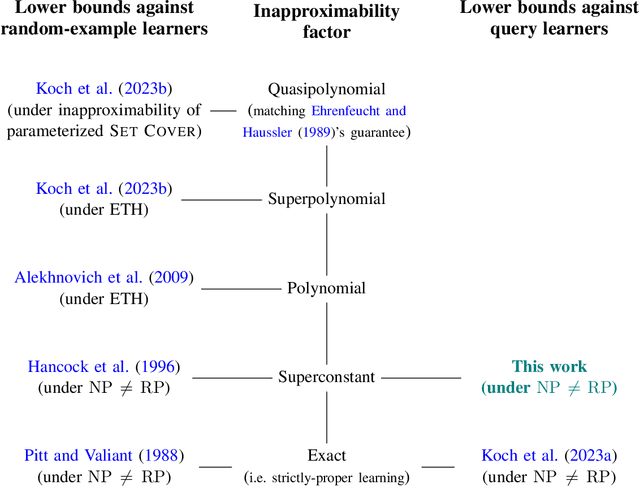
We consider the task of properly PAC learning decision trees with queries. Recent work of Koch, Strassle, and Tan showed that the strictest version of this task, where the hypothesis tree $T$ is required to be optimally small, is NP-hard. Their work leaves open the question of whether the task remains intractable if $T$ is only required to be close to optimal, say within a factor of 2, rather than exactly optimal. We answer this affirmatively and show that the task indeed remains NP-hard even if $T$ is allowed to be within any constant factor of optimal. More generally, our result allows for a smooth tradeoff between the hardness assumption and the inapproximability factor. As Koch et al.'s techniques do not appear to be amenable to such a strengthening, we first recover their result with a new and simpler proof, which we couple with a new XOR lemma for decision trees. While there is a large body of work on XOR lemmas for decision trees, our setting necessitates parameters that are extremely sharp, and are not known to be attainable by existing XOR lemmas. Our work also carries new implications for the related problem of Decision Tree Minimization.

Harnessing the Power of Choices in Decision Tree Learning

We propose a simple generalization of standard and empirically successful decision tree learning algorithms such as ID3, C4.5, and CART. These algorithms, which have been central to machine learning for decades, are greedy in nature: they grow a decision tree by iteratively splitting on the best attribute. Our algorithm, Top-$k$, considers the $k$ best attributes as possible splits instead of just the single best attribute. We demonstrate, theoretically and empirically, the power of this simple generalization. We first prove a {\sl greediness hierarchy theorem} showing that for every $k \in \mathbb{N}$, Top-$(k+1)$ can be dramatically more powerful than Top-$k$: there are data distributions for which the former achieves accuracy $1-\varepsilon$, whereas the latter only achieves accuracy $\frac1{2}+\varepsilon$. We then show, through extensive experiments, that Top-$k$ outperforms the two main approaches to decision tree learning: classic greedy algorithms and more recent "optimal decision tree" algorithms. On one hand, Top-$k$ consistently enjoys significant accuracy gains over greedy algorithms across a wide range of benchmarks. On the other hand, Top-$k$ is markedly more scalable than optimal decision tree algorithms and is able to handle dataset and feature set sizes that remain far beyond the reach of these algorithms.

Properly Learning Decision Trees with Queries Is NP-Hard

We prove that it is NP-hard to properly PAC learn decision trees with queries, resolving a longstanding open problem in learning theory (Bshouty 1993; Guijarro-Lavin-Raghavan 1999; Mehta-Raghavan 2002; Feldman 2016). While there has been a long line of work, dating back to (Pitt-Valiant 1988), establishing the hardness of properly learning decision trees from random examples, the more challenging setting of query learners necessitates different techniques and there were no previous lower bounds. En route to our main result, we simplify and strengthen the best known lower bounds for a different problem of Decision Tree Minimization (Zantema-Bodlaender 2000; Sieling 2003). On a technical level, we introduce the notion of hardness distillation, which we study for decision tree complexity but can be considered for any complexity measure: for a function that requires large decision trees, we give a general method for identifying a small set of inputs that is responsible for its complexity. Our technique even rules out query learners that are allowed constant error. This contrasts with existing lower bounds for the setting of random examples which only hold for inverse-polynomial error. Our result, taken together with a recent almost-polynomial time query algorithm for properly learning decision trees under the uniform distribution (Blanc-Lange-Qiao-Tan 2022), demonstrates the dramatic impact of distributional assumptions on the problem.

Lifting uniform learners via distributional decomposition

We show how any PAC learning algorithm that works under the uniform distribution can be transformed, in a blackbox fashion, into one that works under an arbitrary and unknown distribution $\mathcal{D}$. The efficiency of our transformation scales with the inherent complexity of $\mathcal{D}$, running in $\mathrm{poly}(n, (md)^d)$ time for distributions over $\{\pm 1\}^n$ whose pmfs are computed by depth-$d$ decision trees, where $m$ is the sample complexity of the original algorithm. For monotone distributions our transformation uses only samples from $\mathcal{D}$, and for general ones it uses subcube conditioning samples. A key technical ingredient is an algorithm which, given the aforementioned access to $\mathcal{D}$, produces an optimal decision tree decomposition of $\mathcal{D}$: an approximation of $\mathcal{D}$ as a mixture of uniform distributions over disjoint subcubes. With this decomposition in hand, we run the uniform-distribution learner on each subcube and combine the hypotheses using the decision tree. This algorithmic decomposition lemma also yields new algorithms for learning decision tree distributions with runtimes that exponentially improve on the prior state of the art -- results of independent interest in distribution learning.

Superpolynomial Lower Bounds for Decision Tree Learning and Testing

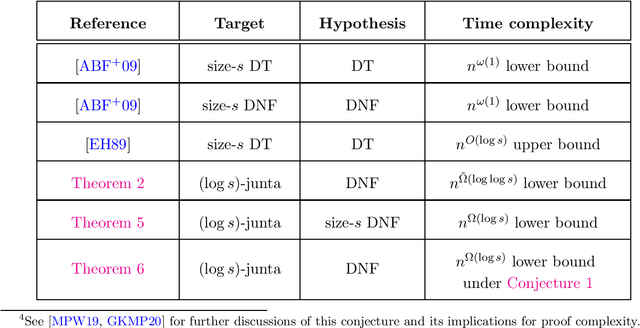
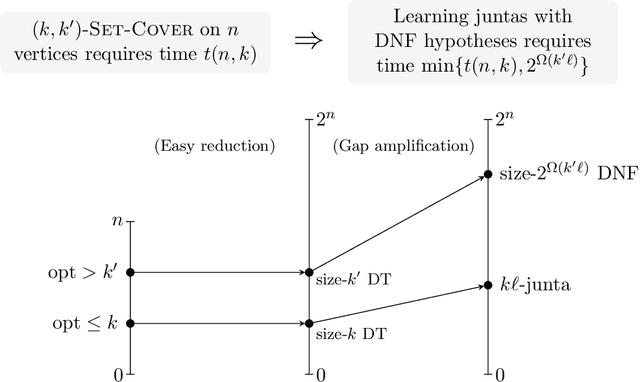
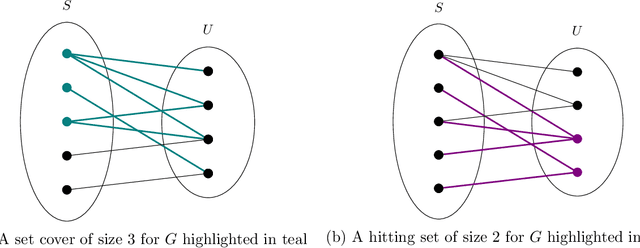
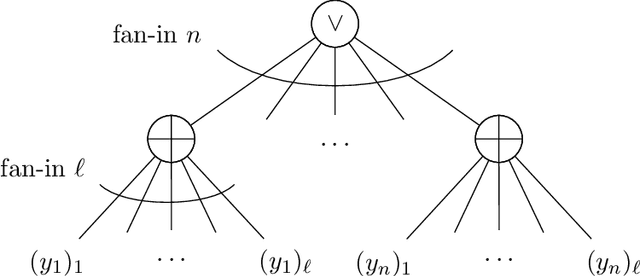
We establish new hardness results for decision tree optimization problems, adding to a line of work that dates back to Hyafil and Rivest in 1976. We prove, under randomized ETH, superpolynomial lower bounds for two basic problems: given an explicit representation of a function $f$ and a generator for a distribution $\mathcal{D}$, construct a small decision tree approximator for $f$ under $\mathcal{D}$, and decide if there is a small decision tree approximator for $f$ under $\mathcal{D}$. Our results imply new lower bounds for distribution-free PAC learning and testing of decision trees, settings in which the algorithm only has restricted access to $f$ and $\mathcal{D}$. Specifically, we show: $n$-variable size-$s$ decision trees cannot be properly PAC learned in time $n^{\tilde{O}(\log\log s)}$, and depth-$d$ decision trees cannot be tested in time $\exp(d^{\,O(1)})$. For learning, the previous best lower bound only ruled out $\text{poly}(n)$-time algorithms (Alekhnovich, Braverman, Feldman, Klivans, and Pitassi, 2009). For testing, recent work gives similar though incomparable bounds in the setting where $f$ is random and $\mathcal{D}$ is nonexplicit (Blais, Ferreira Pinto Jr., and Harms, 2021). Assuming a plausible conjecture on the hardness of Set-Cover, we show our lower bound for learning decision trees can be improved to $n^{\Omega(\log s)}$, matching the best known upper bound of $n^{O(\log s)}$ due to Ehrenfeucht and Haussler (1989). We obtain our results within a unified framework that leverages recent progress in two lines of work: the inapproximability of Set-Cover and XOR lemmas for query complexity. Our framework is versatile and yields results for related concept classes such as juntas and DNF formulas.

Multitask Learning via Shared Features: Algorithms and Hardness

We investigate the computational efficiency of multitask learning of Boolean functions over the $d$-dimensional hypercube, that are related by means of a feature representation of size $k \ll d$ shared across all tasks. We present a polynomial time multitask learning algorithm for the concept class of halfspaces with margin $\gamma$, which is based on a simultaneous boosting technique and requires only $\textrm{poly}(k/\gamma)$ samples-per-task and $\textrm{poly}(k\log(d)/\gamma)$ samples in total. In addition, we prove a computational separation, showing that assuming there exists a concept class that cannot be learned in the attribute-efficient model, we can construct another concept class such that can be learned in the attribute-efficient model, but cannot be multitask learned efficiently -- multitask learning this concept class either requires super-polynomial time complexity or a much larger total number of samples.

A Query-Optimal Algorithm for Finding Counterfactuals

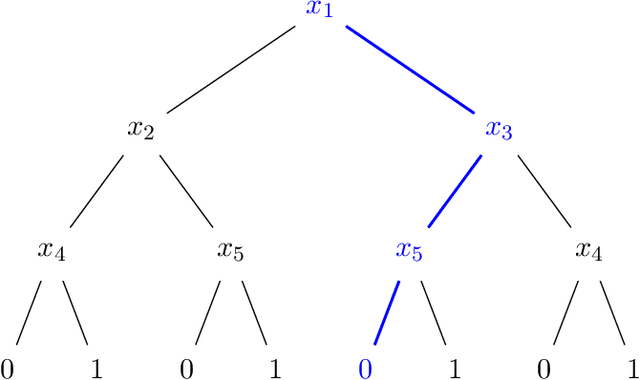
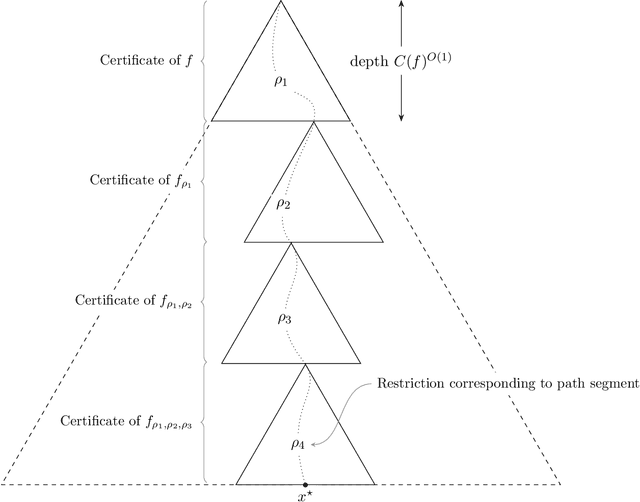
We design an algorithm for finding counterfactuals with strong theoretical guarantees on its performance. For any monotone model $f : X^d \to \{0,1\}$ and instance $x^\star$, our algorithm makes \[ {S(f)^{O(\Delta_f(x^\star))}\cdot \log d}\] queries to $f$ and returns {an {\sl optimal}} counterfactual for $x^\star$: a nearest instance $x'$ to $x^\star$ for which $f(x')\ne f(x^\star)$. Here $S(f)$ is the sensitivity of $f$, a discrete analogue of the Lipschitz constant, and $\Delta_f(x^\star)$ is the distance from $x^\star$ to its nearest counterfactuals. The previous best known query complexity was $d^{\,O(\Delta_f(x^\star))}$, achievable by brute-force local search. We further prove a lower bound of $S(f)^{\Omega(\Delta_f(x^\star))} + \Omega(\log d)$ on the query complexity of any algorithm, thereby showing that the guarantees of our algorithm are essentially optimal.

Open Problem: Properly learning decision trees in polynomial time?

The authors recently gave an $n^{O(\log\log n)}$ time membership query algorithm for properly learning decision trees under the uniform distribution (Blanc et al., 2021). The previous fastest algorithm for this problem ran in $n^{O(\log n)}$ time, a consequence of Ehrenfeucht and Haussler (1989)'s classic algorithm for the distribution-free setting. In this article we highlight the natural open problem of obtaining a polynomial-time algorithm, discuss possible avenues towards obtaining it, and state intermediate milestones that we believe are of independent interest.