CAOTE: KV Caching through Attention Output Error based Token Eviction

While long context support of large language models has extended their abilities, it also incurs challenges in memory and compute which becomes crucial bottlenecks in resource-restricted devices. Token eviction, a widely adopted post-training methodology designed to alleviate the bottlenecks by evicting less important tokens from the cache, typically uses attention scores as proxy metrics for token importance. However, one major limitation of attention score as a token-wise importance metrics is that it lacks the information about contribution of tokens to the attention output. In this paper, we propose a simple eviction criterion based on the contribution of cached tokens to attention outputs. Our method, CAOTE, optimizes for eviction error due to token eviction, by seamlessly integrating attention scores and value vectors. This is the first method which uses value vector information on top of attention-based eviction scores. Additionally, CAOTE can act as a meta-heuristic method with flexible usage with any token eviction method. We show that CAOTE, when combined with the state-of-the-art attention score-based methods, always improves accuracies on the downstream task, indicating the importance of leveraging information from values during token eviction process.

On Speculative Decoding for Multimodal Large Language Models

Inference with Multimodal Large Language Models (MLLMs) is slow due to their large-language-model backbone which suffers from memory bandwidth bottleneck and generates tokens auto-regressively. In this paper, we explore the application of speculative decoding to enhance the inference efficiency of MLLMs, specifically the LLaVA 7B model. We show that a language-only model can serve as a good draft model for speculative decoding with LLaVA 7B, bypassing the need for image tokens and their associated processing components from the draft model. Our experiments across three different tasks show that speculative decoding can achieve a memory-bound speedup of up to 2.37$\times$ using a 115M parameter language model that we trained from scratch. Additionally, we introduce a compact LLaVA draft model incorporating an image adapter, which shows marginal performance gains in image captioning while maintaining comparable results in other tasks.

Direct Alignment of Draft Model for Speculative Decoding with Chat-Fine-Tuned LLMs

Text generation with Large Language Models (LLMs) is known to be memory bound due to the combination of their auto-regressive nature, huge parameter counts, and limited memory bandwidths, often resulting in low token rates. Speculative decoding has been proposed as a solution for LLM inference acceleration. However, since draft models are often unavailable in the modern open-source LLM families, e.g., for Llama 2 7B, training a high-quality draft model is required to enable inference acceleration via speculative decoding. In this paper, we propose a simple draft model training framework for direct alignment to chat-capable target models. With the proposed framework, we train Llama 2 Chat Drafter 115M, a draft model for Llama 2 Chat 7B or larger, with only 1.64\% of the original size. Our training framework only consists of pretraining, distillation dataset generation, and finetuning with knowledge distillation, with no additional alignment procedure. For the finetuning step, we use instruction-response pairs generated by target model for distillation in plausible data distribution, and propose a new Total Variation Distance++ (TVD++) loss that incorporates variance reduction techniques inspired from the policy gradient method in reinforcement learning. Our empirical results show that Llama 2 Chat Drafter 115M with speculative decoding achieves up to 2.3 block efficiency and 2.4$\times$ speed-up relative to autoregressive decoding on various tasks with no further task-specific fine-tuning.

Recursive Speculative Decoding: Accelerating LLM Inference via Sampling Without Replacement

Speculative decoding is an inference-acceleration method for large language models (LLMs) where a small language model generates a draft-token sequence which is further verified by the target LLM in parallel. Recent works have advanced this method by establishing a draft-token tree, achieving superior performance over a single-sequence speculative decoding. However, those works independently generate tokens at each level of the tree, not leveraging the tree's entire diversifiability. Besides, their empirical superiority has been shown for fixed length of sequences, implicitly granting more computational resource to LLM for the tree-based methods. None of the existing works has conducted empirical studies with fixed target computational budgets despite its importance to resource-bounded devices. We present Recursive Speculative Decoding (RSD), a novel tree-based method that samples draft tokens without replacement and maximizes the diversity of the tree. During RSD's drafting, the tree is built by either Gumbel-Top-$k$ trick that draws tokens without replacement in parallel or Stochastic Beam Search that samples sequences without replacement while early-truncating unlikely draft sequences and reducing the computational cost of LLM. We empirically evaluate RSD with Llama 2 and OPT models, showing that RSD outperforms the baseline methods, consistently for fixed draft sequence length and in most cases for fixed computational budgets at LLM.

Neural Topological Ordering for Computation Graphs

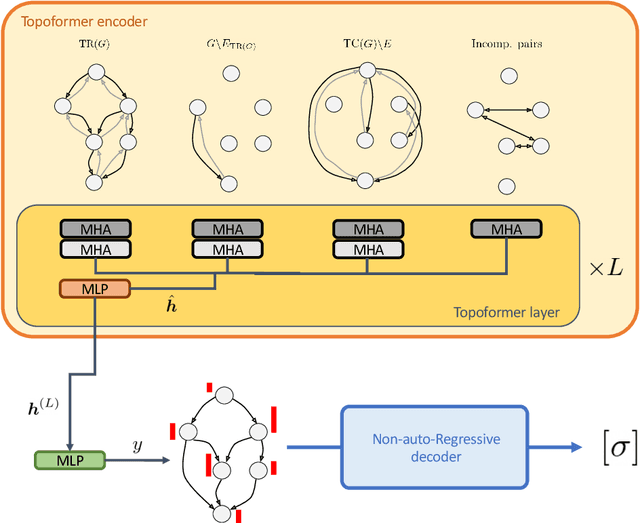
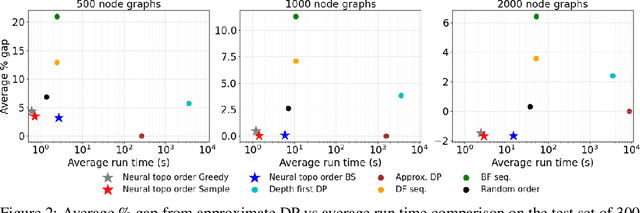
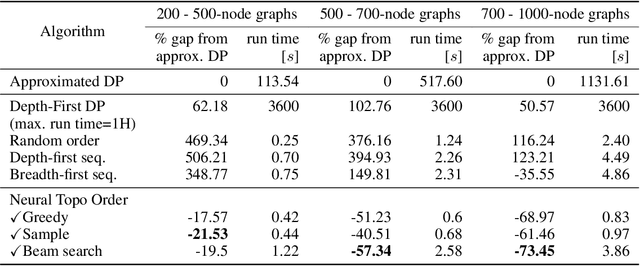
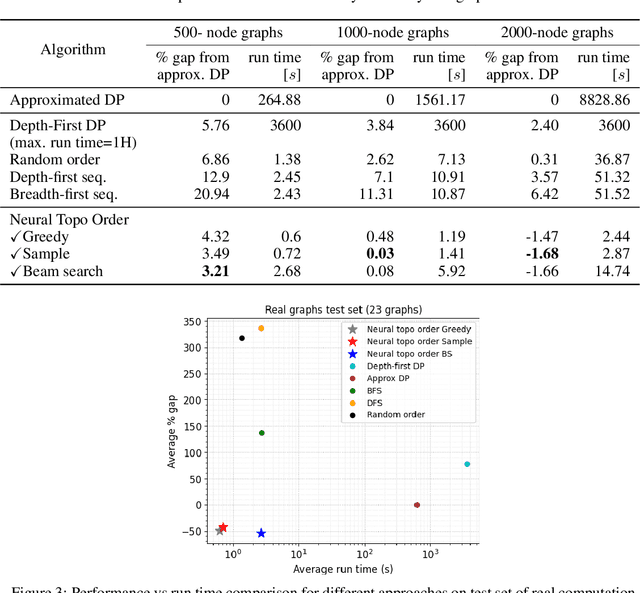
Recent works on machine learning for combinatorial optimization have shown that learning based approaches can outperform heuristic methods in terms of speed and performance. In this paper, we consider the problem of finding an optimal topological order on a directed acyclic graph with focus on the memory minimization problem which arises in compilers. We propose an end-to-end machine learning based approach for topological ordering using an encoder-decoder framework. Our encoder is a novel attention based graph neural network architecture called \emph{Topoformer} which uses different topological transforms of a DAG for message passing. The node embeddings produced by the encoder are converted into node priorities which are used by the decoder to generate a probability distribution over topological orders. We train our model on a dataset of synthetically generated graphs called layered graphs. We show that our model outperforms, or is on-par, with several topological ordering baselines while being significantly faster on synthetic graphs with up to 2k nodes. We also train and test our model on a set of real-world computation graphs, showing performance improvements.

A relaxed technical assumption for posterior sampling-based reinforcement learning for control of unknown linear systems

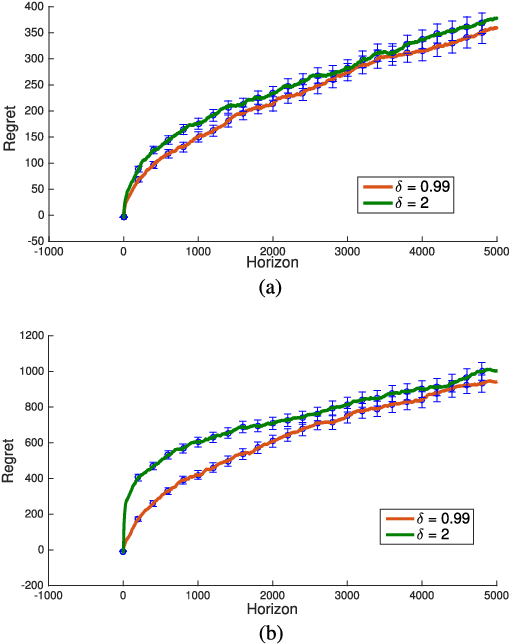
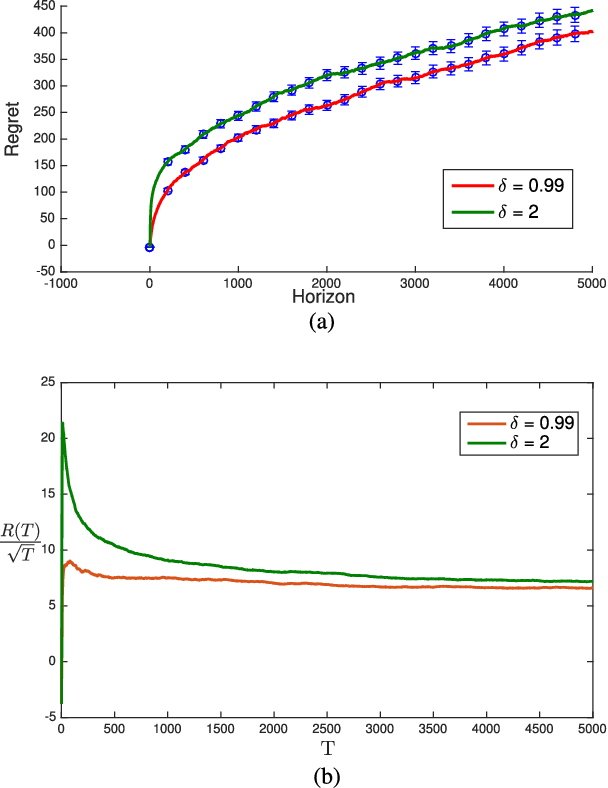
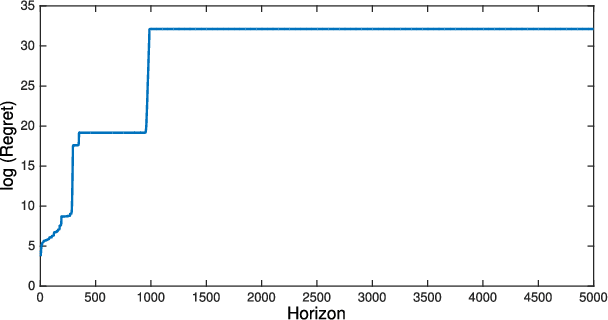
We revisit the Thompson sampling algorithm to control an unknown linear quadratic (LQ) system recently proposed by Ouyang et al (arXiv:1709.04047). The regret bound of the algorithm was derived under a technical assumption on the induced norm of the closed loop system. In this technical note, we show that by making a minor modification in the algorithm (in particular, ensuring that an episode does not end too soon), this technical assumption on the induced norm can be replaced by a milder assumption in terms of the spectral radius of the closed loop system. The modified algorithm has the same Bayesian regret of $\tilde{\mathcal{O}}(\sqrt{T})$, where $T$ is the time-horizon and the $\tilde{\mathcal{O}}(\cdot)$ notation hides logarithmic terms in~$T$.

Thompson sampling for linear quadratic mean-field teams

We consider optimal control of an unknown multi-agent linear quadratic (LQ) system where the dynamics and the cost are coupled across the agents through the mean-field (i.e., empirical mean) of the states and controls. Directly using single-agent LQ learning algorithms in such models results in regret which increases polynomially with the number of agents. We propose a new Thompson sampling based learning algorithm which exploits the structure of the system model and show that the expected Bayesian regret of our proposed algorithm for a system with agents of $|M|$ different types at time horizon $T$ is $\tilde{\mathcal{O}} \big( |M|^{1.5} \sqrt{T} \big)$ irrespective of the total number of agents, where the $\tilde{\mathcal{O}}$ notation hides logarithmic factors in $T$. We present detailed numerical experiments to illustrate the salient features of the proposed algorithm.

Learning Unknown Markov Decision Processes: A Thompson Sampling Approach

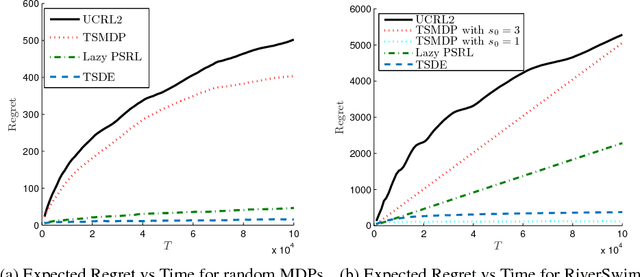
We consider the problem of learning an unknown Markov Decision Process (MDP) that is weakly communicating in the infinite horizon setting. We propose a Thompson Sampling-based reinforcement learning algorithm with dynamic episodes (TSDE). At the beginning of each episode, the algorithm generates a sample from the posterior distribution over the unknown model parameters. It then follows the optimal stationary policy for the sampled model for the rest of the episode. The duration of each episode is dynamically determined by two stopping criteria. The first stopping criterion controls the growth rate of episode length. The second stopping criterion happens when the number of visits to any state-action pair is doubled. We establish $\tilde O(HS\sqrt{AT})$ bounds on expected regret under a Bayesian setting, where $S$ and $A$ are the sizes of the state and action spaces, $T$ is time, and $H$ is the bound of the span. This regret bound matches the best available bound for weakly communicating MDPs. Numerical results show it to perform better than existing algorithms for infinite horizon MDPs.