Neural Topological Ordering for Computation Graphs

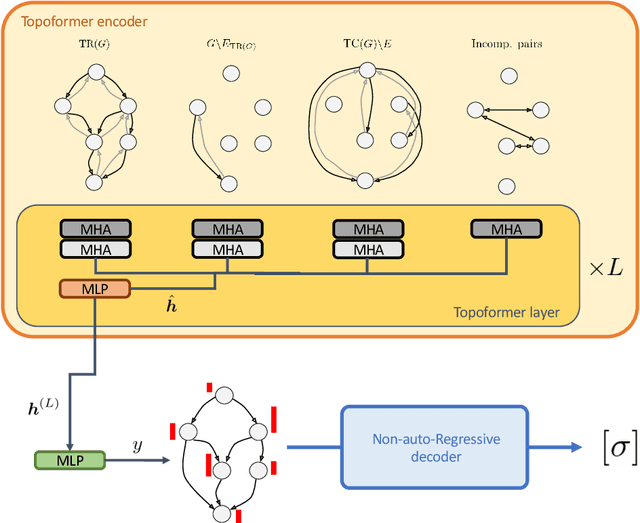
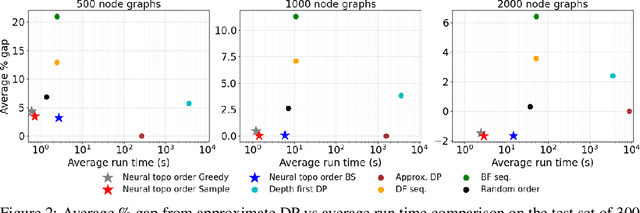
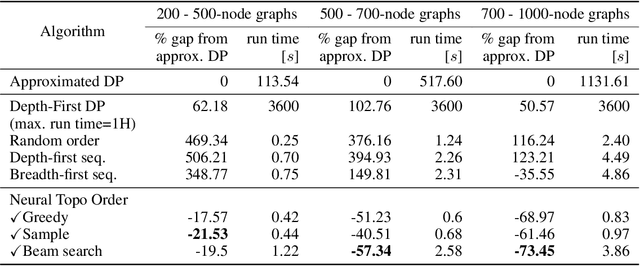
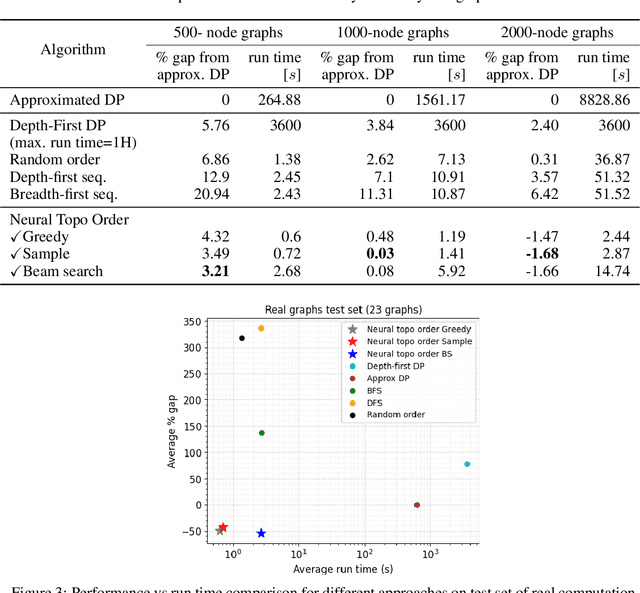
Recent works on machine learning for combinatorial optimization have shown that learning based approaches can outperform heuristic methods in terms of speed and performance. In this paper, we consider the problem of finding an optimal topological order on a directed acyclic graph with focus on the memory minimization problem which arises in compilers. We propose an end-to-end machine learning based approach for topological ordering using an encoder-decoder framework. Our encoder is a novel attention based graph neural network architecture called \emph{Topoformer} which uses different topological transforms of a DAG for message passing. The node embeddings produced by the encoder are converted into node priorities which are used by the decoder to generate a probability distribution over topological orders. We train our model on a dataset of synthetically generated graphs called layered graphs. We show that our model outperforms, or is on-par, with several topological ordering baselines while being significantly faster on synthetic graphs with up to 2k nodes. We also train and test our model on a set of real-world computation graphs, showing performance improvements.

Unifying Variational Inference and PAC-Bayes for Supervised Learning that Scales

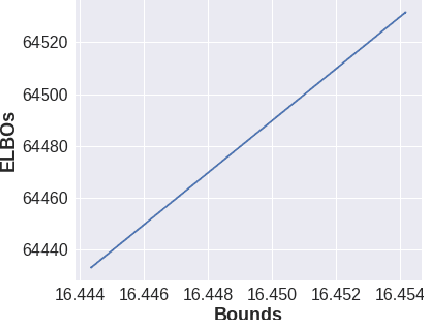
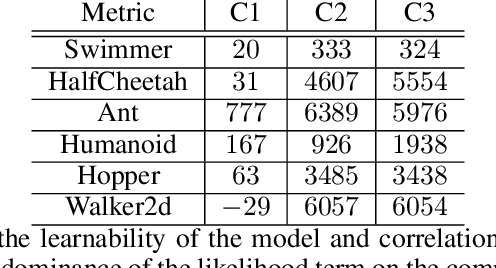
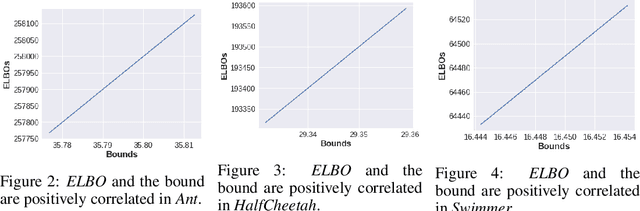
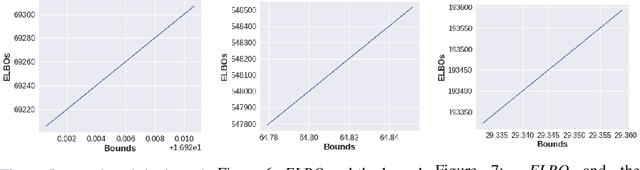
Neural Network based controllers hold enormous potential to learn complex, high-dimensional functions. However, they are prone to overfitting and unwarranted extrapolations. PAC Bayes is a generalized framework which is more resistant to overfitting and that yields performance bounds that hold with arbitrarily high probability even on the unjustified extrapolations. However, optimizing to learn such a function and a bound is intractable for complex tasks. In this work, we propose a method to simultaneously learn such a function and estimate performance bounds that scale organically to high-dimensions, non-linear environments without making any explicit assumptions about the environment. We build our approach on a parallel that we draw between the formulations called ELBO and PAC Bayes when the risk metric is negative log likelihood. Through our experiments on multiple high dimensional MuJoCo locomotion tasks, we validate the correctness of our theory, show its ability to generalize better, and investigate the factors that are important for its learning. The code for all the experiments is available at https://bit.ly/2qv0JjA.