How Efficient is LLM-Generated Code? A Rigorous & High-Standard Benchmark

The emergence of large language models (LLMs) has significantly pushed the frontiers of program synthesis. Advancement of LLM-based program synthesis calls for a thorough evaluation of LLM-generated code. Most evaluation frameworks focus on the (functional) correctness of generated code; efficiency, as an important measure of code quality, has been overlooked in existing evaluations. In this work, we develop ENAMEL (EfficeNcy AutoMatic EvaLuator), a rigorous and high-standard benchmark for evaluating the capability of LLMs in generating efficient code. Firstly, we propose a new efficiency metric called eff@k, which generalizes the pass@k metric from correctness to efficiency and appropriately handles right-censored execution time. Furthermore, we derive an unbiased and variance-reduced estimator of eff@k via Rao--Blackwellization; we also provide a numerically stable implementation for the new estimator. Secondly, to set a high-standard for efficiency evaluation, we employ a human expert to design best algorithms and implementations as our reference solutions of efficiency, many of which are much more efficient than existing canonical solutions in HumanEval and HumanEval+. Moreover, to ensure a rigorous evaluation, we employ a human expert to curate strong test case generators to filter out wrong code and differentiate suboptimal algorithms. An extensive study across 30 popular LLMs using our benchmark ENAMEL shows that LLMs still fall short of generating expert-level efficient code. Using two subsets of our problem set, we demonstrate that such deficiency is because current LLMs struggle in designing advanced algorithms and are barely aware of implementation optimization. Our benchmark is publicly available at https://github.com/q-rz/enamel .

On Speculative Decoding for Multimodal Large Language Models

Inference with Multimodal Large Language Models (MLLMs) is slow due to their large-language-model backbone which suffers from memory bandwidth bottleneck and generates tokens auto-regressively. In this paper, we explore the application of speculative decoding to enhance the inference efficiency of MLLMs, specifically the LLaVA 7B model. We show that a language-only model can serve as a good draft model for speculative decoding with LLaVA 7B, bypassing the need for image tokens and their associated processing components from the draft model. Our experiments across three different tasks show that speculative decoding can achieve a memory-bound speedup of up to 2.37$\times$ using a 115M parameter language model that we trained from scratch. Additionally, we introduce a compact LLaVA draft model incorporating an image adapter, which shows marginal performance gains in image captioning while maintaining comparable results in other tasks.

Direct Alignment of Draft Model for Speculative Decoding with Chat-Fine-Tuned LLMs

Text generation with Large Language Models (LLMs) is known to be memory bound due to the combination of their auto-regressive nature, huge parameter counts, and limited memory bandwidths, often resulting in low token rates. Speculative decoding has been proposed as a solution for LLM inference acceleration. However, since draft models are often unavailable in the modern open-source LLM families, e.g., for Llama 2 7B, training a high-quality draft model is required to enable inference acceleration via speculative decoding. In this paper, we propose a simple draft model training framework for direct alignment to chat-capable target models. With the proposed framework, we train Llama 2 Chat Drafter 115M, a draft model for Llama 2 Chat 7B or larger, with only 1.64\% of the original size. Our training framework only consists of pretraining, distillation dataset generation, and finetuning with knowledge distillation, with no additional alignment procedure. For the finetuning step, we use instruction-response pairs generated by target model for distillation in plausible data distribution, and propose a new Total Variation Distance++ (TVD++) loss that incorporates variance reduction techniques inspired from the policy gradient method in reinforcement learning. Our empirical results show that Llama 2 Chat Drafter 115M with speculative decoding achieves up to 2.3 block efficiency and 2.4$\times$ speed-up relative to autoregressive decoding on various tasks with no further task-specific fine-tuning.

Recursive Speculative Decoding: Accelerating LLM Inference via Sampling Without Replacement

Speculative decoding is an inference-acceleration method for large language models (LLMs) where a small language model generates a draft-token sequence which is further verified by the target LLM in parallel. Recent works have advanced this method by establishing a draft-token tree, achieving superior performance over a single-sequence speculative decoding. However, those works independently generate tokens at each level of the tree, not leveraging the tree's entire diversifiability. Besides, their empirical superiority has been shown for fixed length of sequences, implicitly granting more computational resource to LLM for the tree-based methods. None of the existing works has conducted empirical studies with fixed target computational budgets despite its importance to resource-bounded devices. We present Recursive Speculative Decoding (RSD), a novel tree-based method that samples draft tokens without replacement and maximizes the diversity of the tree. During RSD's drafting, the tree is built by either Gumbel-Top-$k$ trick that draws tokens without replacement in parallel or Stochastic Beam Search that samples sequences without replacement while early-truncating unlikely draft sequences and reducing the computational cost of LLM. We empirically evaluate RSD with Llama 2 and OPT models, showing that RSD outperforms the baseline methods, consistently for fixed draft sequence length and in most cases for fixed computational budgets at LLM.

Moccasin: Efficient Tensor Rematerialization for Neural Networks

The deployment and training of neural networks on edge computing devices pose many challenges. The low memory nature of edge devices is often one of the biggest limiting factors encountered in the deployment of large neural network models. Tensor rematerialization or recompute is a way to address high memory requirements for neural network training and inference. In this paper we consider the problem of execution time minimization of compute graphs subject to a memory budget. In particular, we develop a new constraint programming formulation called \textsc{Moccasin} with only $O(n)$ integer variables, where $n$ is the number of nodes in the compute graph. This is a significant improvement over the works in the recent literature that propose formulations with $O(n^2)$ Boolean variables. We present numerical studies that show that our approach is up to an order of magnitude faster than recent work especially for large-scale graphs.

Neural Topological Ordering for Computation Graphs

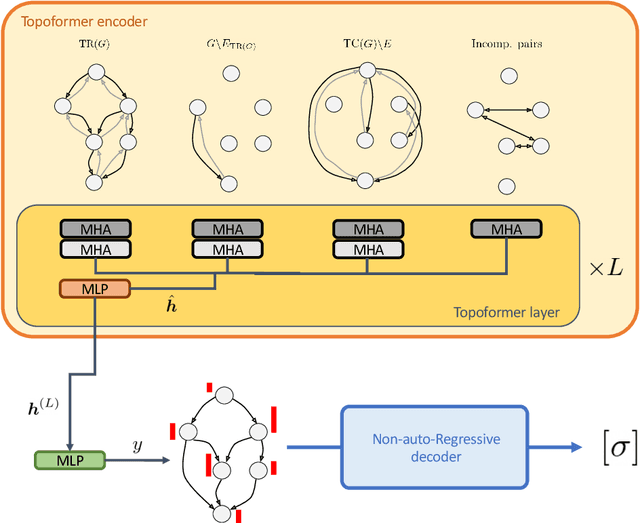
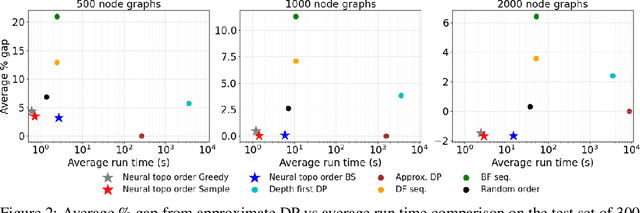
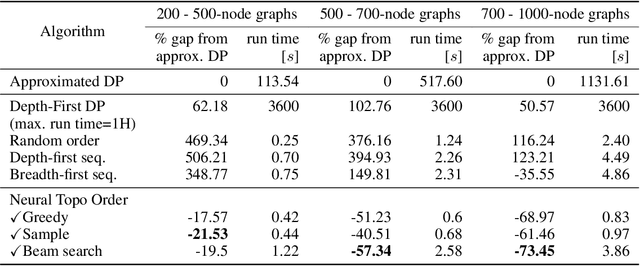
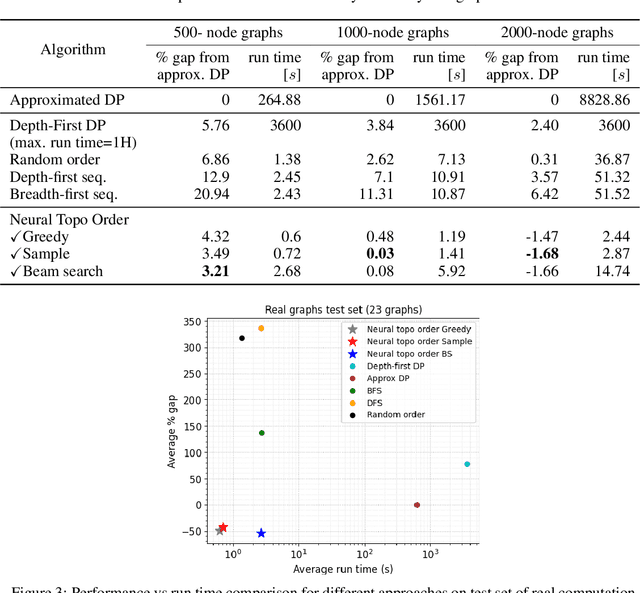
Recent works on machine learning for combinatorial optimization have shown that learning based approaches can outperform heuristic methods in terms of speed and performance. In this paper, we consider the problem of finding an optimal topological order on a directed acyclic graph with focus on the memory minimization problem which arises in compilers. We propose an end-to-end machine learning based approach for topological ordering using an encoder-decoder framework. Our encoder is a novel attention based graph neural network architecture called \emph{Topoformer} which uses different topological transforms of a DAG for message passing. The node embeddings produced by the encoder are converted into node priorities which are used by the decoder to generate a probability distribution over topological orders. We train our model on a dataset of synthetically generated graphs called layered graphs. We show that our model outperforms, or is on-par, with several topological ordering baselines while being significantly faster on synthetic graphs with up to 2k nodes. We also train and test our model on a set of real-world computation graphs, showing performance improvements.