CodeIt: Self-Improving Language Models with Prioritized Hindsight Replay

Large language models are increasingly solving tasks that are commonly believed to require human-level reasoning ability. However, these models still perform very poorly on benchmarks of general intelligence such as the Abstraction and Reasoning Corpus (ARC). In this paper, we approach ARC as a programming-by-examples problem, and introduce a novel and scalable method for language model self-improvement called Code Iteration (CodeIt). Our method iterates between 1) program sampling and hindsight relabeling, and 2) learning from prioritized experience replay. By relabeling the goal of an episode (i.e., the target program output given input) to the realized output produced by the sampled program, our method effectively deals with the extreme sparsity of rewards in program synthesis. Applying CodeIt to the ARC dataset, we demonstrate that prioritized hindsight replay, along with pre-training and data-augmentation, leads to successful inter-task generalization. CodeIt is the first neuro-symbolic approach that scales to the full ARC evaluation dataset. Our method solves 15% of ARC evaluation tasks, achieving state-of-the-art performance and outperforming existing neural and symbolic baselines.

Neural Topological Ordering for Computation Graphs

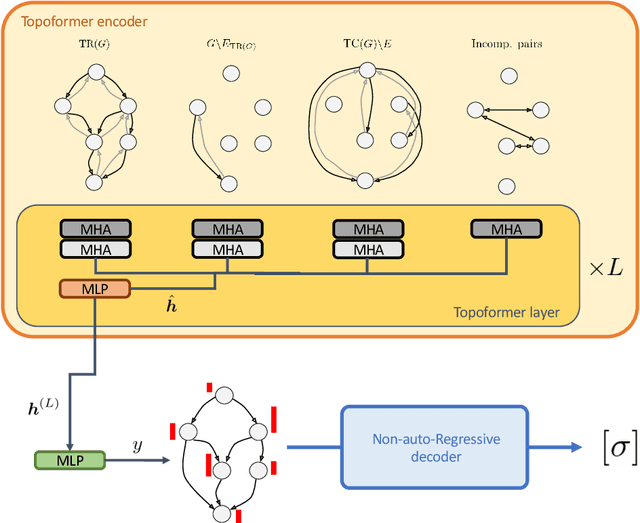
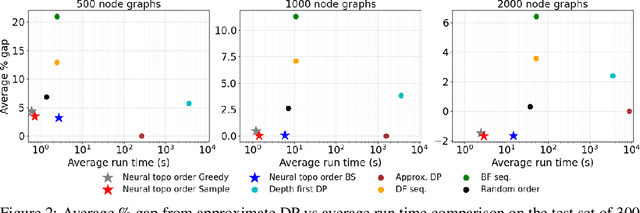
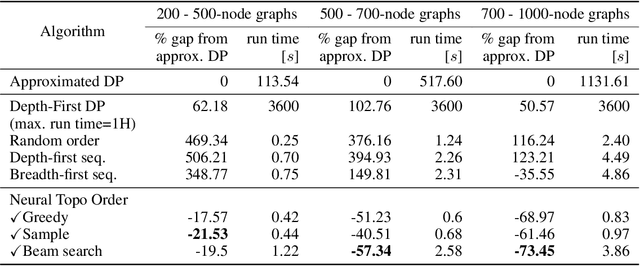
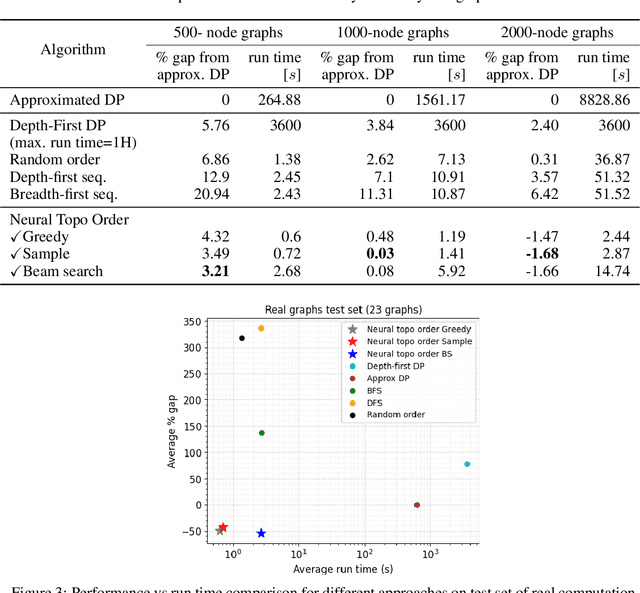
Recent works on machine learning for combinatorial optimization have shown that learning based approaches can outperform heuristic methods in terms of speed and performance. In this paper, we consider the problem of finding an optimal topological order on a directed acyclic graph with focus on the memory minimization problem which arises in compilers. We propose an end-to-end machine learning based approach for topological ordering using an encoder-decoder framework. Our encoder is a novel attention based graph neural network architecture called \emph{Topoformer} which uses different topological transforms of a DAG for message passing. The node embeddings produced by the encoder are converted into node priorities which are used by the decoder to generate a probability distribution over topological orders. We train our model on a dataset of synthetically generated graphs called layered graphs. We show that our model outperforms, or is on-par, with several topological ordering baselines while being significantly faster on synthetic graphs with up to 2k nodes. We also train and test our model on a set of real-world computation graphs, showing performance improvements.

Learning Lattice Quantum Field Theories with Equivariant Continuous Flows

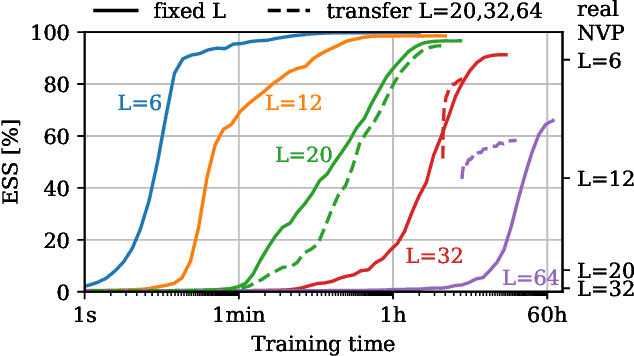
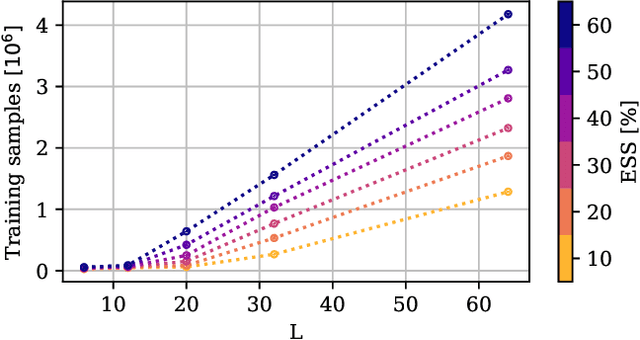
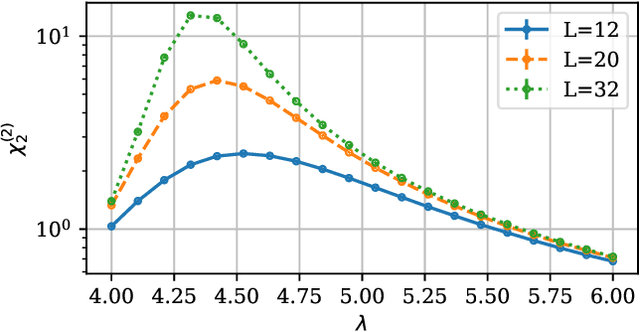
We propose a novel machine learning method for sampling from the high-dimensional probability distributions of Lattice Quantum Field Theories. Instead of the deep architectures used so far for this task, our proposal is based on a single neural ODE layer and incorporates the full symmetries of the problem. We test our model on the $\phi^4$ theory, showing that it systematically outperforms previously proposed flow-based methods in sampling efficiency, and the improvement is especially pronounced for larger lattices. Compared to the previous baseline model, we improve a key metric, the effective sample size, from 1% to 91% on a lattice of size $32\times 32$. We also demonstrate that our model can successfully learn a continuous family of theories at once, and the results of learning can be transferred to larger lattices. Such generalization capacities further accentuate the potential advantages of machine learning methods compared to traditional MCMC-based methods.

Scaling Up Machine Learning For Quantum Field Theory with Equivariant Continuous Flows

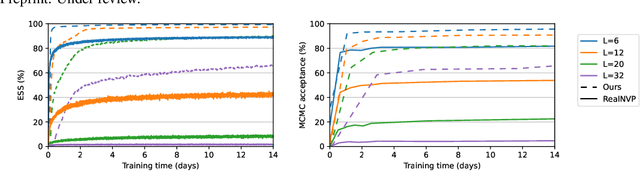
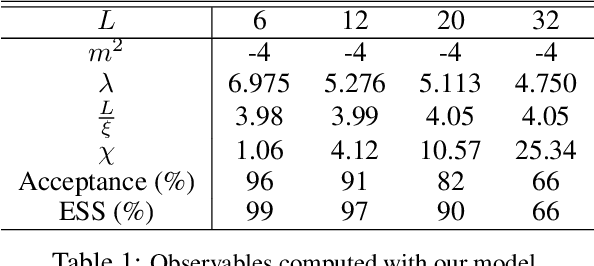
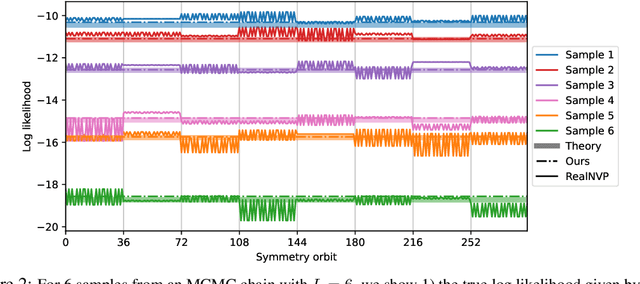
We propose a continuous normalizing flow for sampling from the high-dimensional probability distributions of Quantum Field Theories in Physics. In contrast to the deep architectures used so far for this task, our proposal is based on a shallow design and incorporates the symmetries of the problem. We test our model on the $\phi^4$ theory, showing that it systematically outperforms a realNVP baseline in sampling efficiency, with the difference between the two increasing for larger lattices. On the largest lattice we consider, of size $32\times 32$, we improve a key metric, the effective sample size, from 1% to 66% w.r.t. the realNVP baseline.