Learning Linear Attention in Polynomial Time

Previous research has explored the computational expressivity of Transformer models in simulating Boolean circuits or Turing machines. However, the learnability of these simulators from observational data has remained an open question. Our study addresses this gap by providing the first polynomial-time learnability results (specifically strong, agnostic PAC learning) for single-layer Transformers with linear attention. We show that linear attention may be viewed as a linear predictor in a suitably defined RKHS. As a consequence, the problem of learning any linear transformer may be converted into the problem of learning an ordinary linear predictor in an expanded feature space, and any such predictor may be converted back into a multiheaded linear transformer. Moving to generalization, we show how to efficiently identify training datasets for which every empirical risk minimizer is equivalent (up to trivial symmetries) to the linear Transformer that generated the data, thereby guaranteeing the learned model will correctly generalize across all inputs. Finally, we provide examples of computations expressible via linear attention and therefore polynomial-time learnable, including associative memories, finite automata, and a class of Universal Turing Machine (UTMs) with polynomially bounded computation histories. We empirically validate our theoretical findings on three tasks: learning random linear attention networks, key--value associations, and learning to execute finite automata. Our findings bridge a critical gap between theoretical expressivity and learnability of Transformers, and show that flexible and general models of computation are efficiently learnable.

Are Graph Neural Networks Optimal Approximation Algorithms?

In this work we design graph neural network architectures that can be used to obtain optimal approximation algorithms for a large class of combinatorial optimization problems using powerful algorithmic tools from semidefinite programming (SDP). Concretely, we prove that polynomial-sized message passing algorithms can represent the most powerful polynomial time algorithms for Max Constraint Satisfaction Problems assuming the Unique Games Conjecture. We leverage this result to construct efficient graph neural network architectures, OptGNN, that obtain high-quality approximate solutions on landmark combinatorial optimization problems such as Max Cut and maximum independent set. Our approach achieves strong empirical results across a wide range of real-world and synthetic datasets against both neural baselines and classical algorithms. Finally, we take advantage of OptGNN's ability to capture convex relaxations to design an algorithm for producing dual certificates of optimality (bounds on the optimal solution) from the learned embeddings of OptGNN.

Tensor Decompositions Meet Control Theory: Learning General Mixtures of Linear Dynamical Systems

Recently Chen and Poor initiated the study of learning mixtures of linear dynamical systems. While linear dynamical systems already have wide-ranging applications in modeling time-series data, using mixture models can lead to a better fit or even a richer understanding of underlying subpopulations represented in the data. In this work we give a new approach to learning mixtures of linear dynamical systems that is based on tensor decompositions. As a result, our algorithm succeeds without strong separation conditions on the components, and can be used to compete with the Bayes optimal clustering of the trajectories. Moreover our algorithm works in the challenging partially-observed setting. Our starting point is the simple but powerful observation that the classic Ho-Kalman algorithm is a close relative of modern tensor decomposition methods for learning latent variable models. This gives us a playbook for how to extend it to work with more complicated generative models.

A New Approach to Learning Linear Dynamical Systems

Linear dynamical systems are the foundational statistical model upon which control theory is built. Both the celebrated Kalman filter and the linear quadratic regulator require knowledge of the system dynamics to provide analytic guarantees. Naturally, learning the dynamics of a linear dynamical system from linear measurements has been intensively studied since Rudolph Kalman's pioneering work in the 1960's. Towards these ends, we provide the first polynomial time algorithm for learning a linear dynamical system from a polynomial length trajectory up to polynomial error in the system parameters under essentially minimal assumptions: observability, controllability, and marginal stability. Our algorithm is built on a method of moments estimator to directly estimate Markov parameters from which the dynamics can be extracted. Furthermore, we provide statistical lower bounds when our observability and controllability assumptions are violated.

Approximating Nash Equilibrium in Random Graphical Games

Computing Nash equilibrium in multi-agent games is a longstanding challenge at the interface of game theory and computer science. It is well known that a general normal form game in N players and k strategies requires exponential space simply to write down. This Curse of Multi-Agents prompts the study of succinct games which can be written down efficiently. A canonical example of a succinct game is the graphical game which models players as nodes in a graph interacting with only their neighbors in direct analogy with markov random fields. Graphical games have found applications in wireless, financial, and social networks. However, computing the nash equilbrium of graphical games has proven challenging. Even for polymatrix games, a model where payoffs to an agent can be written as the sum of payoffs of interactions with the agent's neighbors, it has been shown that computing an epsilon approximate nash equilibrium is PPAD hard for epsilon smaller than a constant. The focus of this work is to circumvent this computational hardness by considering average case graph models i.e random graphs. We provide a quasipolynomial time approximation scheme (QPTAS) for computing an epsilon approximate nash equilibrium of polymatrix games on random graphs with edge density greater than poly(k, 1/epsilon, ln(N))$ with high probability. Furthermore, with the same runtime we can compute an epsilon-approximate Nash equilibrium that epsilon-approximates the maximum social welfare of any nash equilibrium of the game. Our primary technical innovation is an "accelerated rounding" of a novel hierarchical convex program for the nash equilibrium problem. Our accelerated rounding also yields faster algorithms for Max-2CSP on the same family of random graphs, which may be of independent interest.

Kalman Filtering with Adversarial Corruptions

Here we revisit the classic problem of linear quadratic estimation, i.e. estimating the trajectory of a linear dynamical system from noisy measurements. The celebrated Kalman filter gives an optimal estimator when the measurement noise is Gaussian, but is widely known to break down when one deviates from this assumption, e.g. when the noise is heavy-tailed. Many ad hoc heuristics have been employed in practice for dealing with outliers. In a pioneering work, Schick and Mitter gave provable guarantees when the measurement noise is a known infinitesimal perturbation of a Gaussian and raised the important question of whether one can get similar guarantees for large and unknown perturbations. In this work we give a truly robust filter: we give the first strong provable guarantees for linear quadratic estimation when even a constant fraction of measurements have been adversarially corrupted. This framework can model heavy-tailed and even non-stationary noise processes. Our algorithm robustifies the Kalman filter in the sense that it competes with the optimal algorithm that knows the locations of the corruptions. Our work is in a challenging Bayesian setting where the number of measurements scales with the complexity of what we need to estimate. Moreover, in linear dynamical systems past information decays over time. We develop a suite of new techniques to robustly extract information across different time steps and over varying time scales.

Online and Distribution-Free Robustness: Regression and Contextual Bandits with Huber Contamination

In this work we revisit two classic high-dimensional online learning problems, namely regression and linear contextual bandits, from the perspective of adversarial robustness. Existing works in algorithmic robust statistics make strong distributional assumptions that ensure that the input data is evenly spread out or comes from a nice generative model. Is it possible to achieve strong robustness guarantees even without distributional assumptions altogether, where the sequence of tasks we are asked to solve is adaptively and adversarially chosen? We answer this question in the affirmative for both regression and linear contextual bandits. In fact our algorithms succeed where convex surrogates fail in the sense that we show strong lower bounds categorically for the existing approaches. Our approach is based on a novel way to use the sum-of-squares hierarchy in online learning and in the absence of distributional assumptions. Moreover we give extensions of our main results to infinite dimensional settings where the feature vectors are represented implicitly via a kernel map.

Classification Under Misspecification: Halfspaces, Generalized Linear Models, and Connections to Evolvability

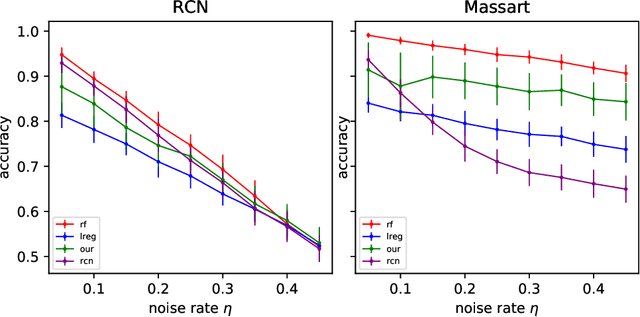
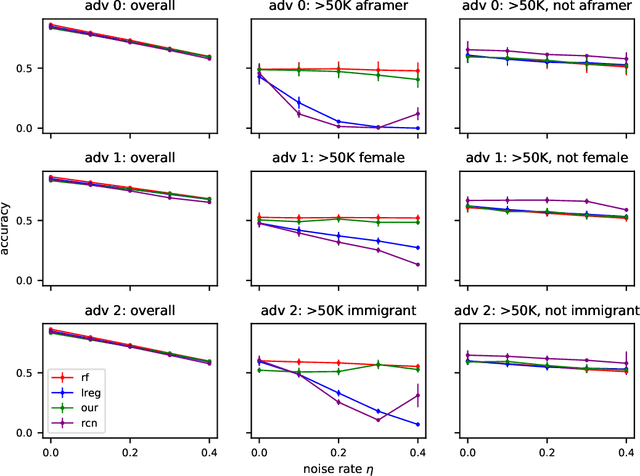
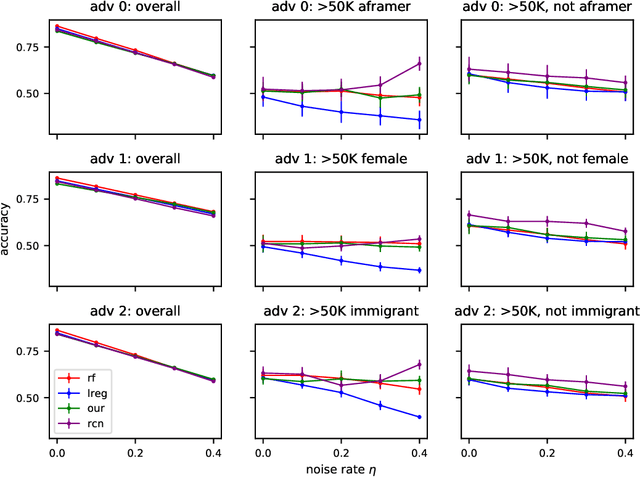
In this paper we revisit some classic problems on classification under misspecification. In particular, we study the problem of learning halfspaces under Massart noise with rate $\eta$. In a recent work, Diakonikolas, Goulekakis, and Tzamos resolved a long-standing problem by giving the first efficient algorithm for learning to accuracy $\eta + \epsilon$ for any $\epsilon > 0$. However, their algorithm outputs a complicated hypothesis, which partitions space into $\text{poly}(d,1/\epsilon)$ regions. Here we give a much simpler algorithm and in the process resolve a number of outstanding open questions: (1) We give the first proper learner for Massart halfspaces that achieves $\eta + \epsilon$. We also give improved bounds on the sample complexity achievable by polynomial time algorithms. (2) Based on (1), we develop a blackbox knowledge distillation procedure to convert an arbitrarily complex classifier to an equally good proper classifier. (3) By leveraging a simple but overlooked connection to evolvability, we show any SQ algorithm requires super-polynomially many queries to achieve $\mathsf{OPT} + \epsilon$. Moreover we study generalized linear models where $\mathbb{E}[Y|\mathbf{X}] = \sigma(\langle \mathbf{w}^*, \mathbf{X}\rangle)$ for any odd, monotone, and Lipschitz function $\sigma$. This family includes the previously mentioned halfspace models as a special case, but is much richer and includes other fundamental models like logistic regression. We introduce a challenging new corruption model that generalizes Massart noise, and give a general algorithm for learning in this setting. Our algorithms are based on a small set of core recipes for learning to classify in the presence of misspecification. Finally we study our algorithm for learning halfspaces under Massart noise empirically and find that it exhibits some appealing fairness properties.