Sequential-Parallel Duality in Prefix Scannable Models

Modern neural sequence models are designed to meet the dual mandate of parallelizable training and fast sequential inference. Recent developments have given rise to various models, such as Gated Linear Attention (GLA) and Mamba, that achieve such ``sequential-parallel duality.'' This raises a natural question: can we characterize the full class of neural sequence models that support near-constant-time parallel evaluation and linear-time, constant-space sequential inference? We begin by describing a broad class of such models -- state space models -- as those whose state updates can be computed using the classic parallel prefix scan algorithm with a custom associative aggregation operator. We then define a more general class, Prefix-Scannable Models (PSMs), by relaxing the state aggregation operator to allow arbitrary (potentially non-associative) functions such as softmax attention. This generalization unifies many existing architectures, including element-wise RNNs (e.g., Mamba) and linear transformers (e.g., GLA, Mamba2, mLSTM), while also introducing new models with softmax-like operators that achieve O(1) amortized compute per token and log(N) memory for sequence length N. We empirically evaluate such models on illustrative small-scale language modeling and canonical synthetic tasks, including state tracking and associative recall. Empirically, we find that PSMs retain the expressivity of transformer-based architectures while matching the inference efficiency of state space models -- in some cases exhibiting better length generalization than either.

Parallel Algorithms Align with Neural Execution

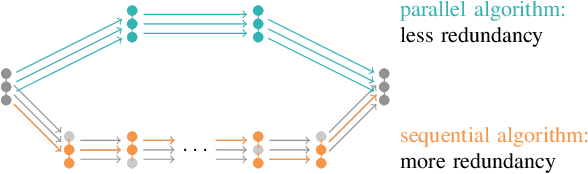
Neural algorithmic reasoners are parallel processors. Teaching them sequential algorithms contradicts this nature, rendering a significant share of their computations redundant. Parallel algorithms however may exploit their full computational power, therefore requiring fewer layers to be executed. This drastically reduces training times, as we observe when comparing parallel implementations of searching, sorting and finding strongly connected components to their sequential counterparts on the CLRS framework. Additionally, parallel versions achieve strongly superior predictive performance in most cases.