Universal Rates of ERM for Agnostic Learning

The universal learning framework has been developed to obtain guarantees on the learning rates that hold for any fixed distribution, which can be much faster than the ones uniformly hold over all the distributions. Given that the Empirical Risk Minimization (ERM) principle being fundamental in the PAC theory and ubiquitous in practical machine learning, the recent work of arXiv:2412.02810 studied the universal rates of ERM for binary classification under the realizable setting. However, the assumption of realizability is too restrictive to hold in practice. Indeed, the majority of the literature on universal learning has focused on the realizable case, leaving the non-realizable case barely explored. In this paper, we consider the problem of universal learning by ERM for binary classification under the agnostic setting, where the ''learning curve" reflects the decay of the excess risk as the sample size increases. We explore the possibilities of agnostic universal rates and reveal a compact trichotomy: there are three possible agnostic universal rates of ERM, being either $e^{-n}$, $o(n^{-1/2})$, or arbitrarily slow. We provide a complete characterization of which concept classes fall into each of these categories. Moreover, we also establish complete characterizations for the target-dependent universal rates as well as the Bayes-dependent universal rates.

Rethinking Gradient-based Adversarial Attacks on Point Cloud Classification

Gradient-based adversarial attacks have become a dominant approach for evaluating the robustness of point cloud classification models. However, existing methods often rely on uniform update rules that fail to consider the heterogeneous nature of point clouds, resulting in excessive and perceptible perturbations. In this paper, we rethink the design of gradient-based attacks by analyzing the limitations of conventional gradient update mechanisms and propose two new strategies to improve both attack effectiveness and imperceptibility. First, we introduce WAAttack, a novel framework that incorporates weighted gradients and an adaptive step-size strategy to account for the non-uniform contribution of points during optimization. This approach enables more targeted and subtle perturbations by dynamically adjusting updates according to the local structure and sensitivity of each point. Second, we propose SubAttack, a complementary strategy that decomposes the point cloud into subsets and focuses perturbation efforts on structurally critical regions. Together, these methods represent a principled rethinking of gradient-based adversarial attacks for 3D point cloud classification. Extensive experiments demonstrate that our approach outperforms state-of-the-art baselines in generating highly imperceptible adversarial examples. Code will be released upon paper acceptance.

LexPam: Legal Procedure Awareness-Guided Mathematical Reasoning

The legal mathematical reasoning ability of LLMs is crucial when applying them to real-world scenarios, as it directly affects the credibility of the LLM. While existing legal LLMs can perform general judicial question answering, their legal mathematical reasoning capabilities have not been trained. Open-domain reasoning models, though able to generate detailed calculation steps, do not follow the reasoning logic required for legal scenarios. Additionally, there is currently a lack of legal mathematical reasoning datasets to help validate and enhance LLMs' reasoning abilities in legal contexts. To address these issues, we propose the first Chinese legal Mathematical Reasoning Dataset, LexNum, which includes three common legal mathematical reasoning scenarios: economic compensation, work injury compensation, and traffic accident compensation. Based on LexNum, we tested the performance of existing legal LLMs and reasoning LLMs, and introduced LexPam, a reinforcement learning algorithm guided by legal procedural awareness to train LLMs, enhancing their mathematical reasoning abilities in legal scenarios. Experiments on tasks in the three legal scenarios show that the performance of existing legal LLMs and reasoning models in legal mathematical reasoning tasks is unsatisfactory. LexPam can enhance the LLM's ability in these tasks.

Universal Rates of Empirical Risk Minimization

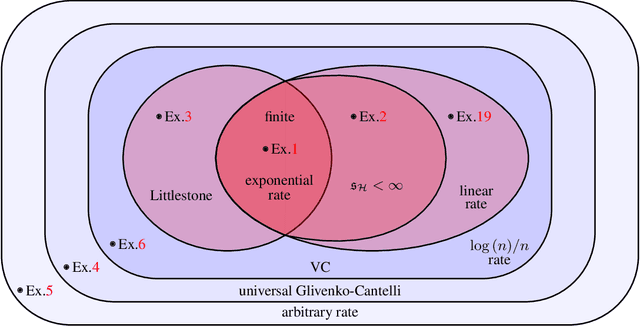
The well-known empirical risk minimization (ERM) principle is the basis of many widely used machine learning algorithms, and plays an essential role in the classical PAC theory. A common description of a learning algorithm's performance is its so-called "learning curve", that is, the decay of the expected error as a function of the input sample size. As the PAC model fails to explain the behavior of learning curves, recent research has explored an alternative universal learning model and has ultimately revealed a distinction between optimal universal and uniform learning rates (Bousquet et al., 2021). However, a basic understanding of such differences with a particular focus on the ERM principle has yet to be developed. In this paper, we consider the problem of universal learning by ERM in the realizable case and study the possible universal rates. Our main result is a fundamental tetrachotomy: there are only four possible universal learning rates by ERM, namely, the learning curves of any concept class learnable by ERM decay either at $e^{-n}$, $1/n$, $\log(n)/n$, or arbitrarily slow rates. Moreover, we provide a complete characterization of which concept classes fall into each of these categories, via new complexity structures. We also develop new combinatorial dimensions which supply sharp asymptotically-valid constant factors for these rates, whenever possible.

Efficient Estimation of the Central Mean Subspace via Smoothed Gradient Outer Products

We consider the problem of sufficient dimension reduction (SDR) for multi-index models. The estimators of the central mean subspace in prior works either have slow (non-parametric) convergence rates, or rely on stringent distributional conditions (e.g., the covariate distribution $P_{\mathbf{X}}$ being elliptical symmetric). In this paper, we show that a fast parametric convergence rate of form $C_d \cdot n^{-1/2}$ is achievable via estimating the \emph{expected smoothed gradient outer product}, for a general class of distribution $P_{\mathbf{X}}$ admitting Gaussian or heavier distributions. When the link function is a polynomial with a degree of at most $r$ and $P_{\mathbf{X}}$ is the standard Gaussian, we show that the prefactor depends on the ambient dimension $d$ as $C_d \propto d^r$.

Distributed Semi-Supervised Sparse Statistical Inference

This paper is devoted to studying the semi-supervised sparse statistical inference in a distributed setup. An efficient multi-round distributed debiased estimator, which integrates both labeled and unlabelled data, is developed. We will show that the additional unlabeled data helps to improve the statistical rate of each round of iteration. Our approach offers tailored debiasing methods for $M$-estimation and generalized linear model according to the specific form of the loss function. Our method also applies to a non-smooth loss like absolute deviation loss. Furthermore, our algorithm is computationally efficient since it requires only one estimation of a high-dimensional inverse covariance matrix. We demonstrate the effectiveness of our method by presenting simulation studies and real data applications that highlight the benefits of incorporating unlabeled data.