Efficient Estimation of the Central Mean Subspace via Smoothed Gradient Outer Products

We consider the problem of sufficient dimension reduction (SDR) for multi-index models. The estimators of the central mean subspace in prior works either have slow (non-parametric) convergence rates, or rely on stringent distributional conditions (e.g., the covariate distribution $P_{\mathbf{X}}$ being elliptical symmetric). In this paper, we show that a fast parametric convergence rate of form $C_d \cdot n^{-1/2}$ is achievable via estimating the \emph{expected smoothed gradient outer product}, for a general class of distribution $P_{\mathbf{X}}$ admitting Gaussian or heavier distributions. When the link function is a polynomial with a degree of at most $r$ and $P_{\mathbf{X}}$ is the standard Gaussian, we show that the prefactor depends on the ambient dimension $d$ as $C_d \propto d^r$.

Nuances in Margin Conditions Determine Gains in Active Learning

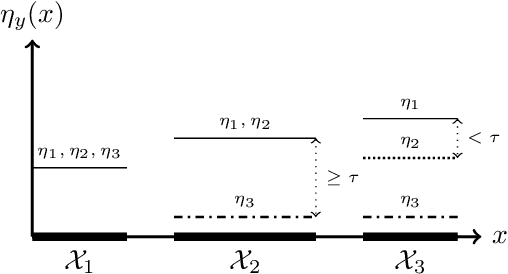
We consider nonparametric classification with smooth regression functions, where it is well known that notions of margin in $E[Y|X]$ determine fast or slow rates in both active and passive learning. Here we elucidate a striking distinction between the two settings. Namely, we show that some seemingly benign nuances in notions of margin -- involving the uniqueness of the Bayes classifier, and which have no apparent effect on rates in passive learning -- determine whether or not any active learner can outperform passive learning rates. In particular, for Audibert-Tsybakov's margin condition (allowing general situations with non-unique Bayes classifiers), no active learner can gain over passive learning in commonly studied settings where the marginal on $X$ is near uniform. Our results thus negate the usual intuition from past literature that active rates should improve over passive rates in nonparametric settings.

Weakly Supervised Learning Creates a Fusion of Modeling Cultures

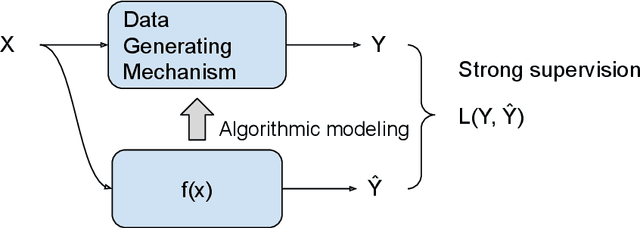
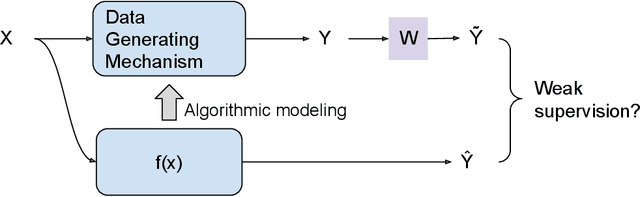
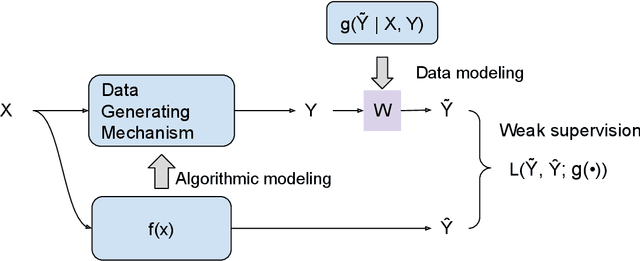
The past two decades have witnessed the great success of the algorithmic modeling framework advocated by Breiman et al. (2001). Nevertheless, the excellent prediction performance of these black-box models rely heavily on the availability of strong supervision, i.e. a large set of accurate and exact ground-truth labels. In practice, strong supervision can be unavailable or expensive, which calls for modeling techniques under weak supervision. In this comment, we summarize the key concepts in weakly supervised learning and discuss some recent developments in the field. Using algorithmic modeling alone under a weak supervision might lead to unstable and misleading results. A promising direction would be integrating the data modeling culture into such a framework.