Cryptographic Hardness of Score Estimation

We show that $L^2$-accurate score estimation, in the absence of strong assumptions on the data distribution, is computationally hard even when sample complexity is polynomial in the relevant problem parameters. Our reduction builds on the result of Chen et al. (ICLR 2023), who showed that the problem of generating samples from an unknown data distribution reduces to $L^2$-accurate score estimation. Our hard-to-estimate distributions are the "Gaussian pancakes" distributions, originally due to Diakonikolas et al. (FOCS 2017), which have been shown to be computationally indistinguishable from the standard Gaussian under widely believed hardness assumptions from lattice-based cryptography (Bruna et al., STOC 2021; Gupte et al., FOCS 2022).

Learning Single-Index Models with Shallow Neural Networks

Single-index models are a class of functions given by an unknown univariate ``link'' function applied to an unknown one-dimensional projection of the input. These models are particularly relevant in high dimension, when the data might present low-dimensional structure that learning algorithms should adapt to. While several statistical aspects of this model, such as the sample complexity of recovering the relevant (one-dimensional) subspace, are well-understood, they rely on tailored algorithms that exploit the specific structure of the target function. In this work, we introduce a natural class of shallow neural networks and study its ability to learn single-index models via gradient flow. More precisely, we consider shallow networks in which biases of the neurons are frozen at random initialization. We show that the corresponding optimization landscape is benign, which in turn leads to generalization guarantees that match the near-optimal sample complexity of dedicated semi-parametric methods.

Lattice-Based Methods Surpass Sum-of-Squares in Clustering

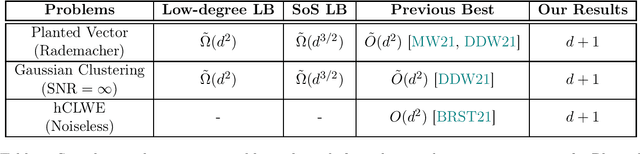
Clustering is a fundamental primitive in unsupervised learning which gives rise to a rich class of computationally-challenging inference tasks. In this work, we focus on the canonical task of clustering d-dimensional Gaussian mixtures with unknown (and possibly degenerate) covariance. Recent works (Ghosh et al. '20; Mao, Wein '21; Davis, Diaz, Wang '21) have established lower bounds against the class of low-degree polynomial methods and the sum-of-squares (SoS) hierarchy for recovering certain hidden structures planted in Gaussian clustering instances. Prior work on many similar inference tasks portends that such lower bounds strongly suggest the presence of an inherent statistical-to-computational gap for clustering, that is, a parameter regime where the clustering task is statistically possible but no polynomial-time algorithm succeeds. One special case of the clustering task we consider is equivalent to the problem of finding a planted hypercube vector in an otherwise random subspace. We show that, perhaps surprisingly, this particular clustering model does not exhibit a statistical-to-computational gap, even though the aforementioned low-degree and SoS lower bounds continue to apply in this case. To achieve this, we give a polynomial-time algorithm based on the Lenstra--Lenstra--Lovasz lattice basis reduction method which achieves the statistically-optimal sample complexity of d+1 samples. This result extends the class of problems whose conjectured statistical-to-computational gaps can be "closed" by "brittle" polynomial-time algorithms, highlighting the crucial but subtle role of noise in the onset of statistical-to-computational gaps.

On the Cryptographic Hardness of Learning Single Periodic Neurons

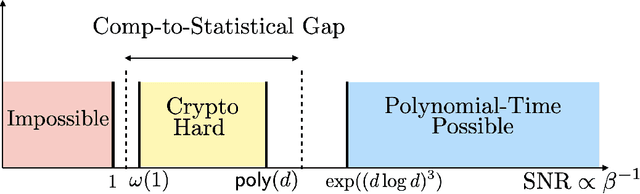
We show a simple reduction which demonstrates the cryptographic hardness of learning a single periodic neuron over isotropic Gaussian distributions in the presence of noise. More precisely, our reduction shows that any polynomial-time algorithm (not necessarily gradient-based) for learning such functions under small noise implies a polynomial-time quantum algorithm for solving worst-case lattice problems, whose hardness form the foundation of lattice-based cryptography. Our core hard family of functions, which are well-approximated by one-layer neural networks, take the general form of a univariate periodic function applied to an affine projection of the data. These functions have appeared in previous seminal works which demonstrate their hardness against gradient-based (Shamir'18), and Statistical Query (SQ) algorithms (Song et al.'17). We show that if (polynomially) small noise is added to the labels, the intractability of learning these functions applies to all polynomial-time algorithms under the aforementioned cryptographic assumptions. Moreover, we demonstrate the necessity of noise in the hardness result by designing a polynomial-time algorithm for learning certain families of such functions under exponentially small adversarial noise. Our proposed algorithm is not a gradient-based or an SQ algorithm, but is rather based on the celebrated Lenstra-Lenstra-Lov\'asz (LLL) lattice basis reduction algorithm. Furthermore, in the absence of noise, this algorithm can be directly applied to solve CLWE detection (Bruna et al.'21) and phase retrieval with an optimal sample complexity of $d+1$ samples. In the former case, this improves upon the quadratic-in-$d$ sample complexity required in (Bruna et al.'21). In the latter case, this improves upon the state-of-the-art AMP-based algorithm, which requires approximately $1.128d$ samples (Barbier et al.'19).

Self-Supervised Motion Retargeting with Safety Guarantee

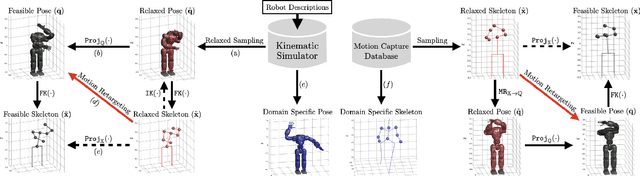
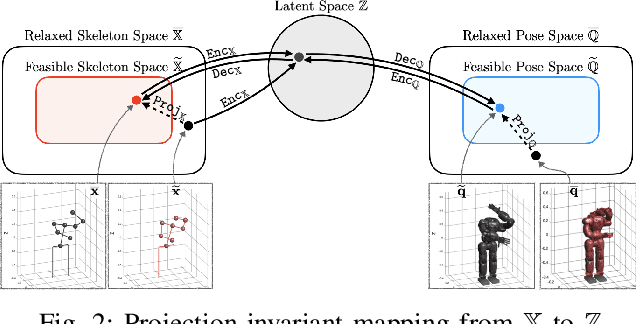
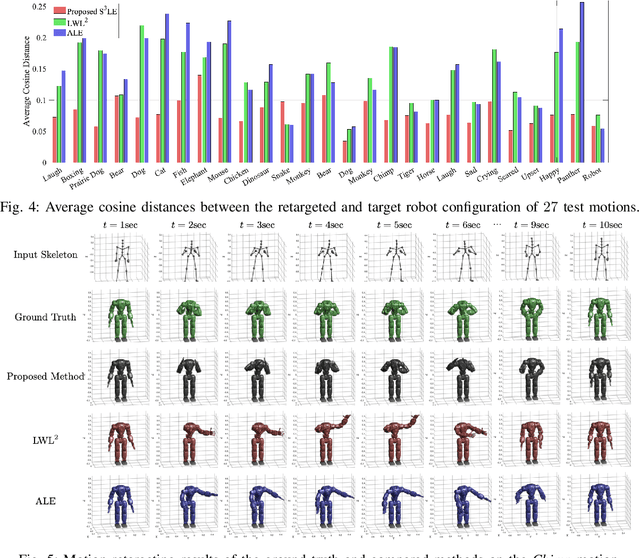
In this paper, we present self-supervised shared latent embedding (S3LE), a data-driven motion retargeting method that enables the generation of natural motions in humanoid robots from motion capture data or RGB videos. While it requires paired data consisting of human poses and their corresponding robot configurations, it significantly alleviates the necessity of time-consuming data-collection via novel paired data generating processes. Our self-supervised learning procedure consists of two steps: automatically generating paired data to bootstrap the motion retargeting, and learning a projection-invariant mapping to handle the different expressivity of humans and humanoid robots. Furthermore, our method guarantees that the generated robot pose is collision-free and satisfies position limits by utilizing nonparametric regression in the shared latent space. We demonstrate that our method can generate expressive robotic motions from both the CMU motion capture database and YouTube videos.

Evaluating representations by the complexity of learning low-loss predictors

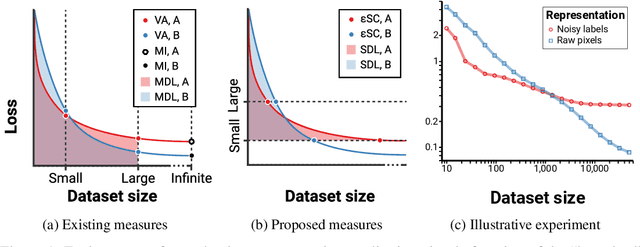
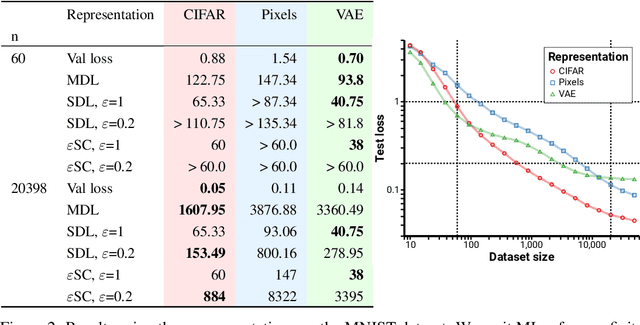
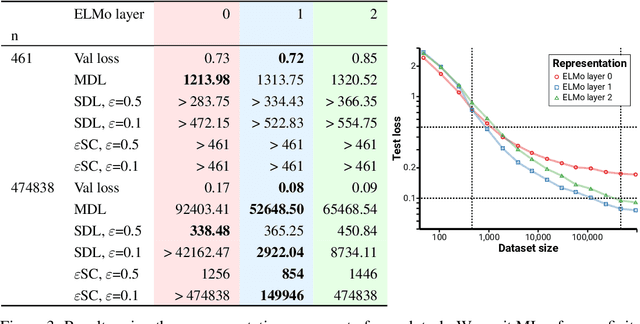
We consider the problem of evaluating representations of data for use in solving a downstream task. We propose to measure the quality of a representation by the complexity of learning a predictor on top of the representation that achieves low loss on a task of interest, and introduce two methods, surplus description length (SDL) and $\varepsilon$ sample complexity ($\varepsilon$SC). In contrast to prior methods, which measure the amount of information about the optimal predictor that is present in a specific amount of data, our methods measure the amount of information needed from the data to recover an approximation of the optimal predictor up to a specified tolerance. We present a framework to compare these methods based on plotting the validation loss versus training set size (the "loss-data" curve). Existing measures, such as mutual information and minimum description length probes, correspond to slices and integrals along the data-axis of the loss-data curve, while ours correspond to slices and integrals along the loss-axis. We provide experiments on real data to compare the behavior of each of these methods over datasets of varying size along with a high performance open source library for representation evaluation at https://github.com/willwhitney/reprieve.

Continuous LWE

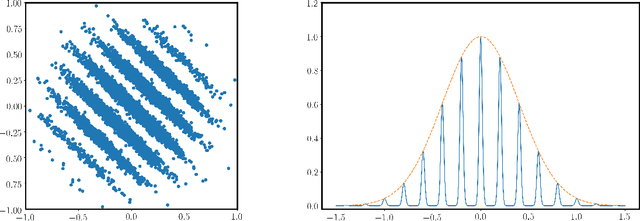
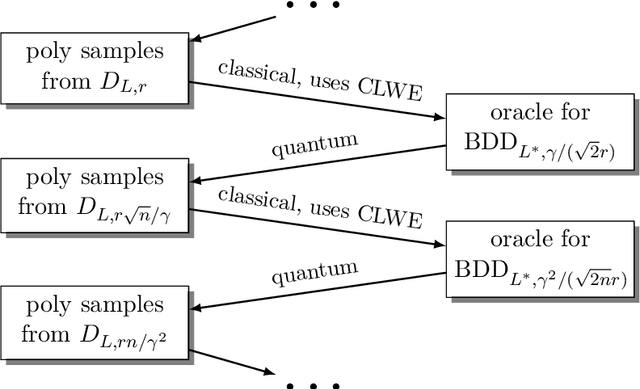
We introduce a continuous analogue of the Learning with Errors (LWE) problem, which we name CLWE. We give a polynomial-time quantum reduction from worst-case lattice problems to CLWE, showing that CLWE enjoys similar hardness guarantees to those of LWE. Alternatively, our result can also be seen as opening new avenues of (quantum) attacks on lattice problems. Our work resolves an open problem regarding the computational complexity of learning mixtures of Gaussians without separability assumptions (Diakonikolas 2016, Moitra 2018). As an additional motivation, (a slight variant of) CLWE was considered in the context of robust machine learning (Diakonikolas et al.~FOCS 2017), where hardness in the statistical query (SQ) model was shown; our work addresses the open question regarding its computational hardness (Bubeck et al.~ICML 2019).