Continuous LWE

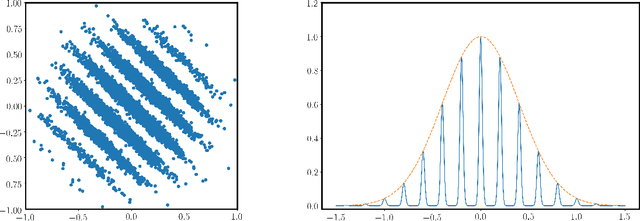
We introduce a continuous analogue of the Learning with Errors (LWE) problem, which we name CLWE. We give a polynomial-time quantum reduction from worst-case lattice problems to CLWE, showing that CLWE enjoys similar hardness guarantees to those of LWE. Alternatively, our result can also be seen as opening new avenues of (quantum) attacks on lattice problems. Our work resolves an open problem regarding the computational complexity of learning mixtures of Gaussians without separability assumptions (Diakonikolas 2016, Moitra 2018). As an additional motivation, (a slight variant of) CLWE was considered in the context of robust machine learning (Diakonikolas et al.~FOCS 2017), where hardness in the statistical query (SQ) model was shown; our work addresses the open question regarding its computational hardness (Bubeck et al.~ICML 2019).

On Learning Mixtures of Well-Separated Gaussians

We consider the problem of efficiently learning mixtures of a large number of spherical Gaussians, when the components of the mixture are well separated. In the most basic form of this problem, we are given samples from a uniform mixture of $k$ standard spherical Gaussians, and the goal is to estimate the means up to accuracy $\delta$ using $poly(k,d, 1/\delta)$ samples. In this work, we study the following question: what is the minimum separation needed between the means for solving this task? The best known algorithm due to Vempala and Wang [JCSS 2004] requires a separation of roughly $\min\{k,d\}^{1/4}$. On the other hand, Moitra and Valiant [FOCS 2010] showed that with separation $o(1)$, exponentially many samples are required. We address the significant gap between these two bounds, by showing the following results. 1. We show that with separation $o(\sqrt{\log k})$, super-polynomially many samples are required. In fact, this holds even when the $k$ means of the Gaussians are picked at random in $d=O(\log k)$ dimensions. 2. We show that with separation $\Omega(\sqrt{\log k})$, $poly(k,d,1/\delta)$ samples suffice. Note that the bound on the separation is independent of $\delta$. This result is based on a new and efficient "accuracy boosting" algorithm that takes as input coarse estimates of the true means and in time $poly(k,d, 1/\delta)$ outputs estimates of the means up to arbitrary accuracy $\delta$ assuming the separation between the means is $\Omega(\min\{\sqrt{\log k},\sqrt{d}\})$ (independently of $\delta$). We also present a computationally efficient algorithm in $d=O(1)$ dimensions with only $\Omega(\sqrt{d})$ separation. These results together essentially characterize the optimal order of separation between components that is needed to learn a mixture of $k$ spherical Gaussians with polynomial samples.