Practical Full Resolution Learned Lossless Image Compression

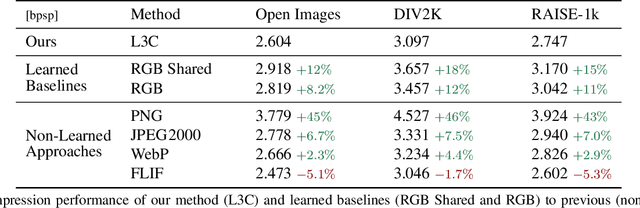
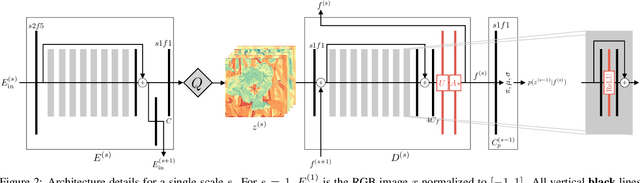
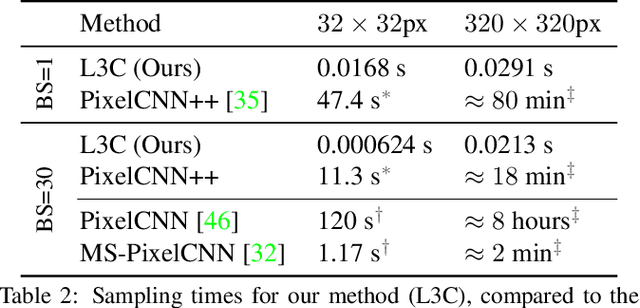
We propose the first practical learned lossless image compression system, L3C, and show that it outperforms the popular engineered codecs, PNG, WebP and JPEG2000. At the core of our method is a fully parallelizable hierarchical probabilistic model for adaptive entropy coding which is optimized end-to-end for the compression task. In contrast to recent autoregressive discrete probabilistic models such as PixelCNN, our method i) models the image distribution jointly with learned auxiliary representations instead of exclusively modeling the image distribution in RGB space, and ii) only requires three forward-passes to predict all pixel probabilities instead of one for each pixel. As a result, L3C obtains over three orders of magnitude speedups compared to the fastest PixelCNN variant (Multiscale-PixelCNN). Furthermore, we find that learning the auxiliary representation is crucial and outperforms predefined auxiliary representations such as an RGB pyramid significantly.

Deep Generative Models for Distribution-Preserving Lossy Compression

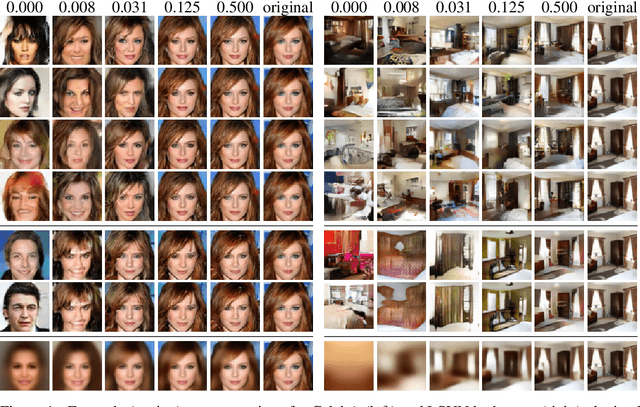
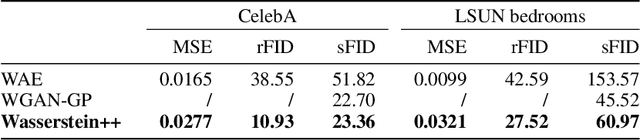
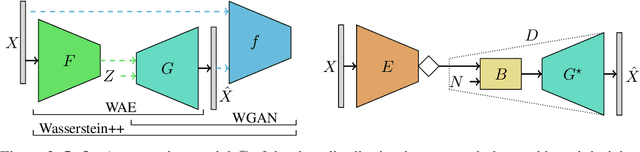
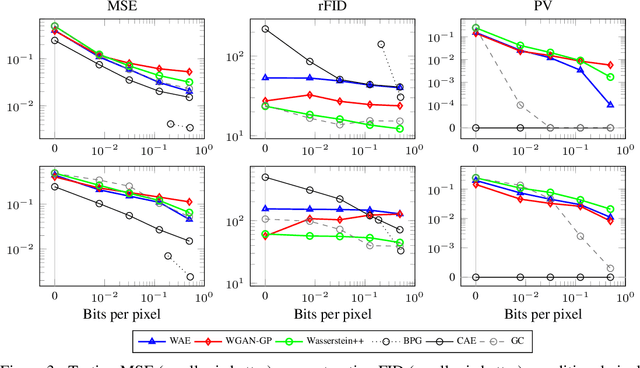
We propose and study the problem of distribution-preserving lossy compression. Motivated by recent advances in extreme image compression which allow to maintain artifact-free reconstructions even at very low bitrates, we propose to optimize the rate-distortion tradeoff under the constraint that the reconstructed samples follow the distribution of the training data. The resulting compression system recovers both ends of the spectrum: On one hand, at zero bitrate it learns a generative model of the data, and at high enough bitrates it achieves perfect reconstruction. Furthermore, for intermediate bitrates it smoothly interpolates between learning a generative model of the training data and perfectly reconstructing the training samples. We study several methods to approximately solve the proposed optimization problem, including a novel combination of Wasserstein GAN and Wasserstein Autoencoder, and present an extensive theoretical and empirical characterization of the proposed compression systems.

Generative Adversarial Networks for Extreme Learned Image Compression

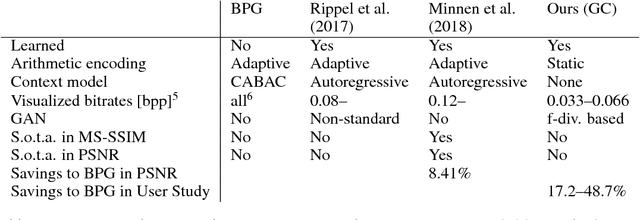
We propose a framework for extreme learned image compression based on Generative Adversarial Networks (GANs), obtaining visually pleasing images at significantly lower bitrates than previous methods. This is made possible through our GAN formulation of learned compression combined with a generator/decoder which operates on the full-resolution image and is trained in combination with a multi-scale discriminator. Additionally, if a semantic label map of the original image is available, our method can fully synthesize unimportant regions in the decoded image such as streets and trees from the label map, therefore only requiring the storage of the preserved region and the semantic label map. A user study confirms that for low bitrates, our approach is preferred to state-of-the-art methods, even when they use more than double the bits.

Born Again Neural Networks

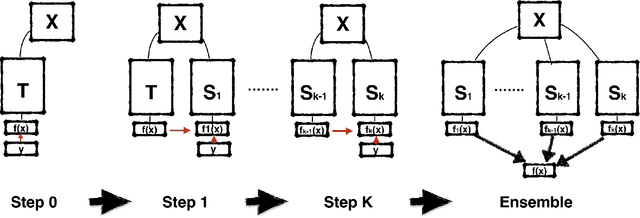
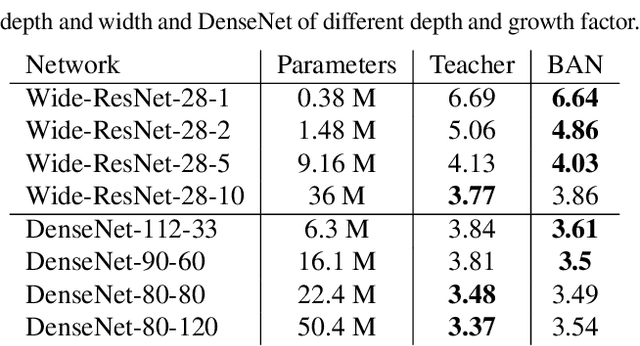
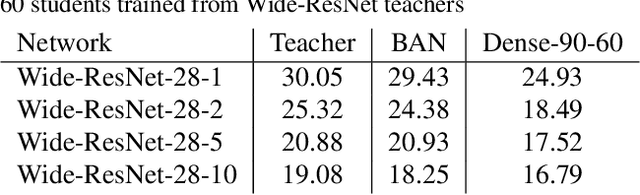
Knowledge distillation (KD) consists of transferring knowledge from one machine learning model (the teacher}) to another (the student). Commonly, the teacher is a high-capacity model with formidable performance, while the student is more compact. By transferring knowledge, one hopes to benefit from the student's compactness. %we desire a compact model with performance close to the teacher's. We study KD from a new perspective: rather than compressing models, we train students parameterized identically to their teachers. Surprisingly, these {Born-Again Networks (BANs), outperform their teachers significantly, both on computer vision and language modeling tasks. Our experiments with BANs based on DenseNets demonstrate state-of-the-art performance on the CIFAR-10 (3.5%) and CIFAR-100 (15.5%) datasets, by validation error. Additional experiments explore two distillation objectives: (i) Confidence-Weighted by Teacher Max (CWTM) and (ii) Dark Knowledge with Permuted Predictions (DKPP). Both methods elucidate the essential components of KD, demonstrating a role of the teacher outputs on both predicted and non-predicted classes. We present experiments with students of various capacities, focusing on the under-explored case where students overpower teachers. Our experiments show significant advantages from transferring knowledge between DenseNets and ResNets in either direction.

Noisy subspace clustering via matching pursuits

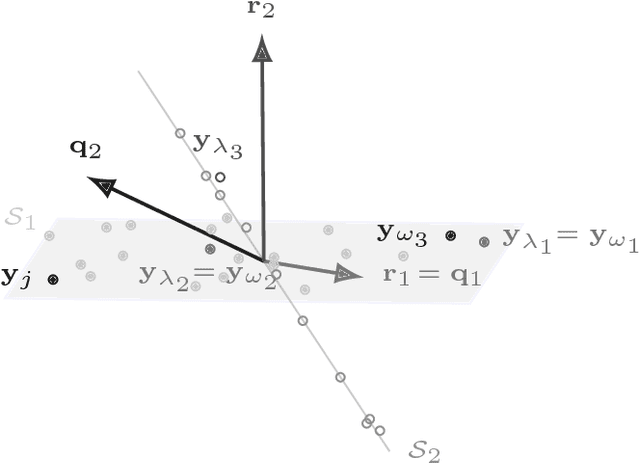
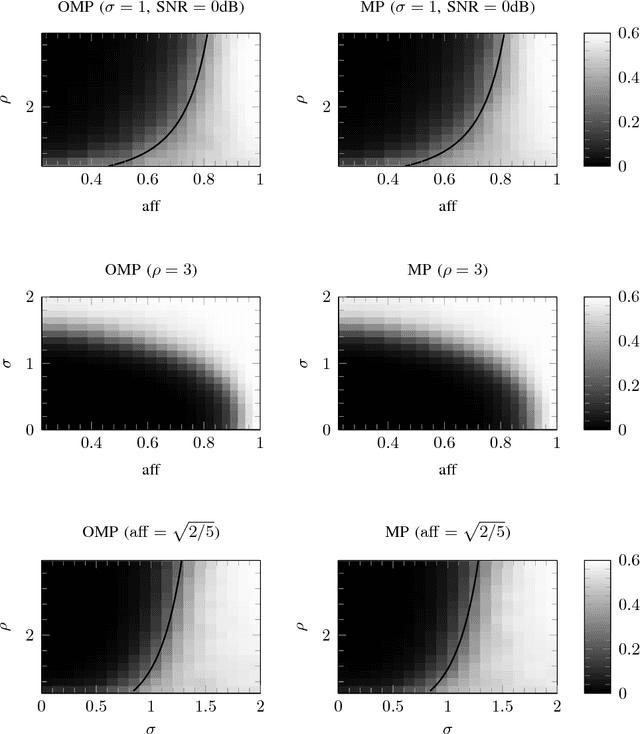
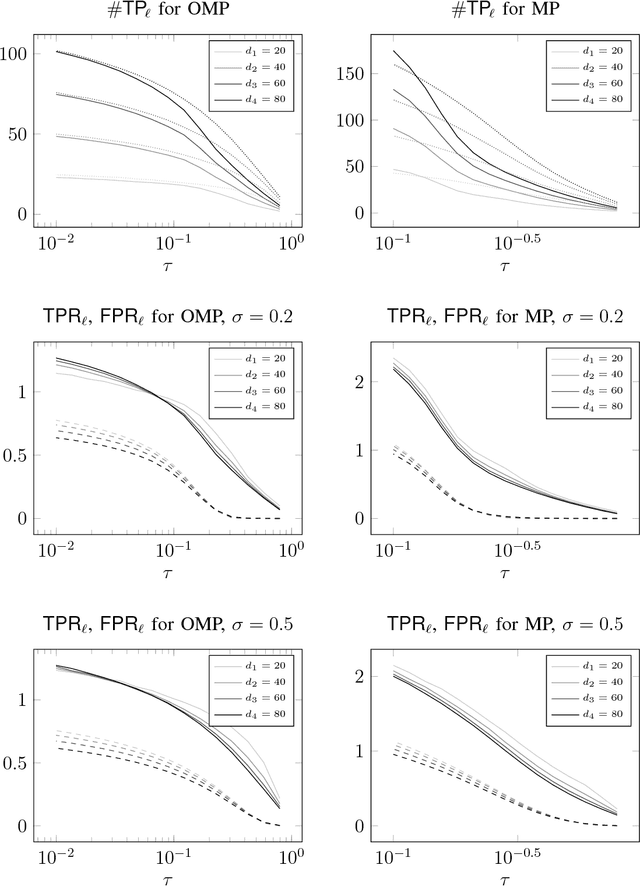
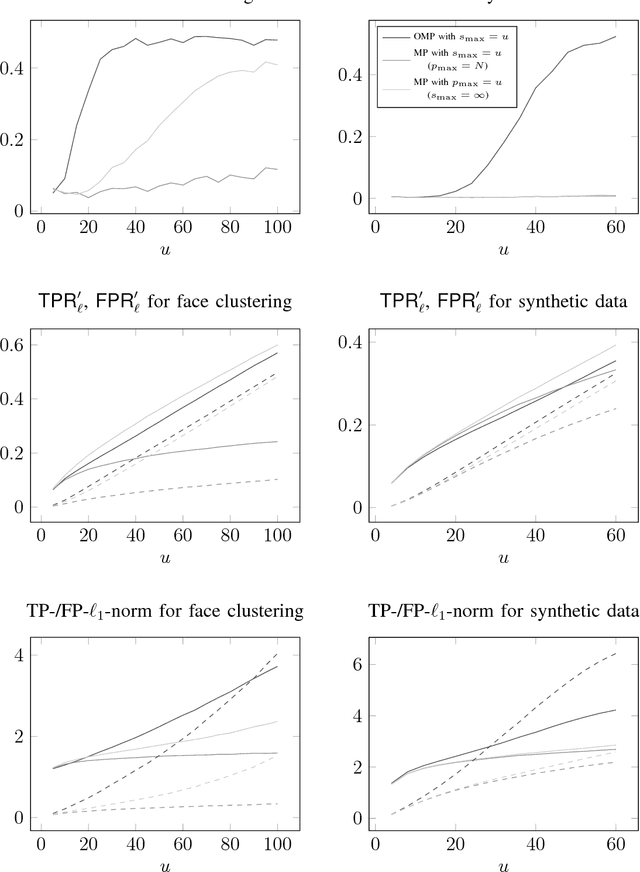
Sparsity-based subspace clustering algorithms have attracted significant attention thanks to their excellent performance in practical applications. A prominent example is the sparse subspace clustering (SSC) algorithm by Elhamifar and Vidal, which performs spectral clustering based on an adjacency matrix obtained by sparsely representing each data point in terms of all the other data points via the Lasso. When the number of data points is large or the dimension of the ambient space is high, the computational complexity of SSC quickly becomes prohibitive. Dyer et al. observed that SSC-OMP obtained by replacing the Lasso by the greedy orthogonal matching pursuit (OMP) algorithm results in significantly lower computational complexity, while often yielding comparable performance. The central goal of this paper is an analytical performance characterization of SSC-OMP for noisy data. Moreover, we introduce and analyze the SSC-MP algorithm, which employs matching pursuit (MP) in lieu of OMP. Both SSC-OMP and SSC-MP are proven to succeed even when the subspaces intersect and when the data points are contaminated by severe noise. The clustering conditions we obtain for SSC-OMP and SSC-MP are similar to those for SSC and for the thresholding-based subspace clustering (TSC) algorithm due to Heckel and B\"olcskei. Analytical results in combination with numerical results indicate that both SSC-OMP and SSC-MP with a data-dependent stopping criterion automatically detect the dimensions of the subspaces underlying the data. Moreover, experiments on synthetic and on real data show that SSC-MP compares very favorably to SSC, SSC-OMP, TSC, and the nearest subspace neighbor algorithm, both in terms of clustering performance and running time. In addition, we find that, in contrast to SSC-OMP, the performance of SSC-MP is very robust with respect to the choice of parameters in the stopping criteria.

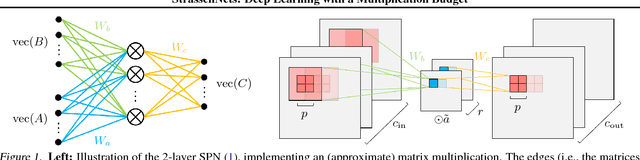
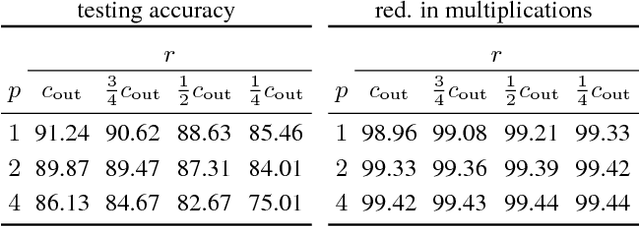
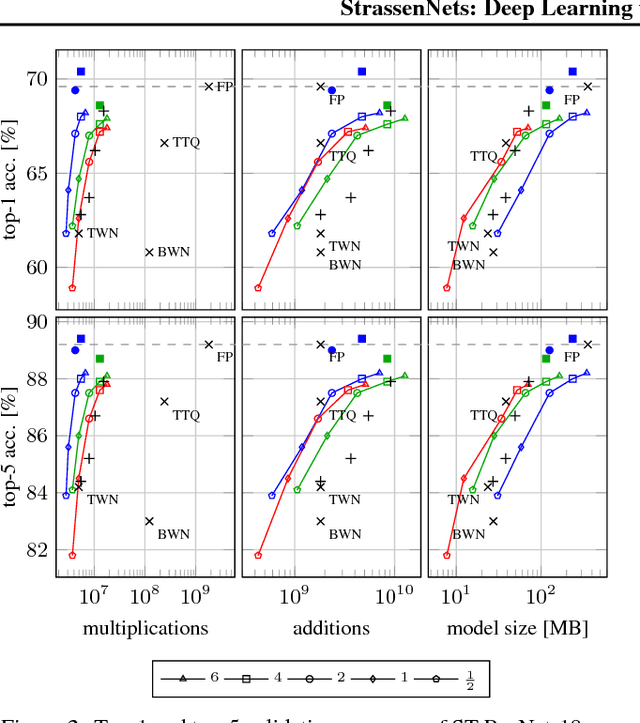
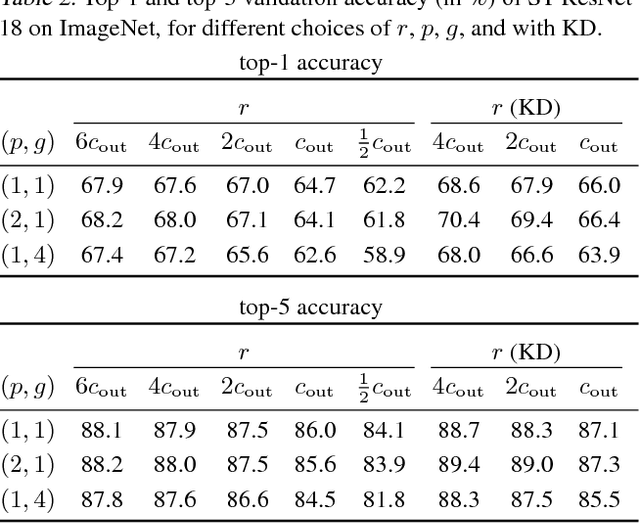
StrassenNets: Deep Learning with a Multiplication Budget

A large fraction of the arithmetic operations required to evaluate deep neural networks (DNNs) consists of matrix multiplications, in both convolution and fully connected layers. We perform end-to-end learning of low-cost approximations of matrix multiplications in DNN layers by casting matrix multiplications as 2-layer sum-product networks (SPNs) (arithmetic circuits) and learning their (ternary) edge weights from data. The SPNs disentangle multiplication and addition operations and enable us to impose a budget on the number of multiplication operations. Combining our method with knowledge distillation and applying it to image classification DNNs (trained on ImageNet) and language modeling DNNs (using LSTMs), we obtain a first-of-a-kind reduction in number of multiplications (over 99.5%) while maintaining the predictive performance of the full-precision models. Finally, we demonstrate that the proposed framework is able to rediscover Strassen's matrix multiplication algorithm, learning to multiply $2 \times 2$ matrices using only 7 multiplications instead of 8.

Conditional Probability Models for Deep Image Compression

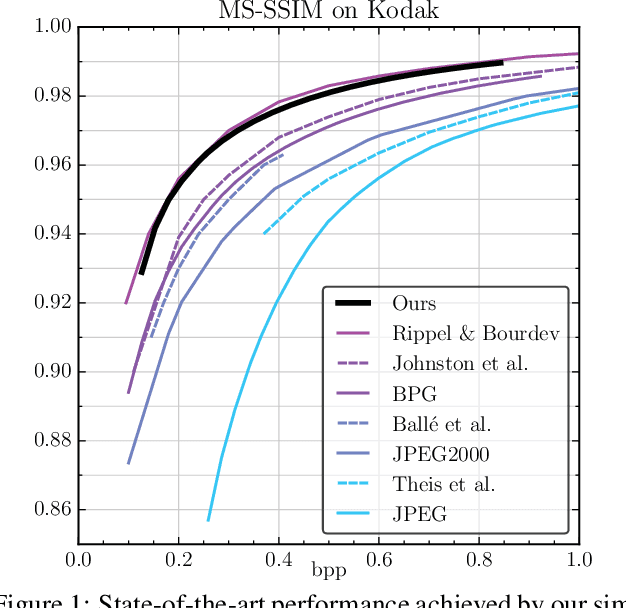
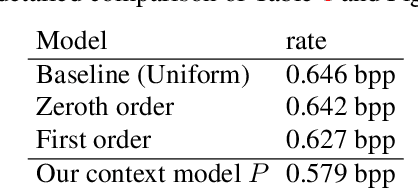
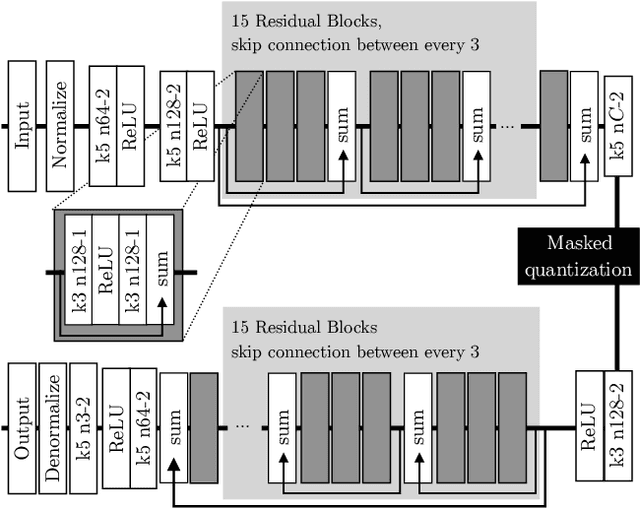
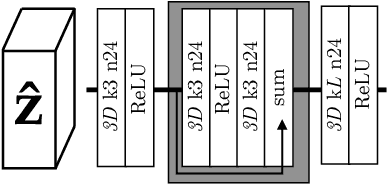
Deep Neural Networks trained as image auto-encoders have recently emerged as a promising direction for advancing the state-of-the-art in image compression. The key challenge in learning such networks is twofold: To deal with quantization, and to control the trade-off between reconstruction error (distortion) and entropy (rate) of the latent image representation. In this paper, we focus on the latter challenge and propose a new technique to navigate the rate-distortion trade-off for an image compression auto-encoder. The main idea is to directly model the entropy of the latent representation by using a context model: A 3D-CNN which learns a conditional probability model of the latent distribution of the auto-encoder. During training, the auto-encoder makes use of the context model to estimate the entropy of its representation, and the context model is concurrently updated to learn the dependencies between the symbols in the latent representation. Our experiments show that this approach, when measured in MS-SSIM, yields a state-of-the-art image compression system based on a simple convolutional auto-encoder.

Convolutional Recurrent Neural Networks for Electrocardiogram Classification

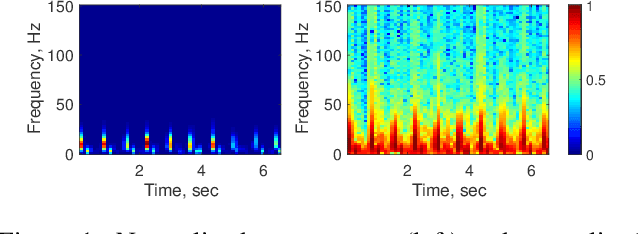
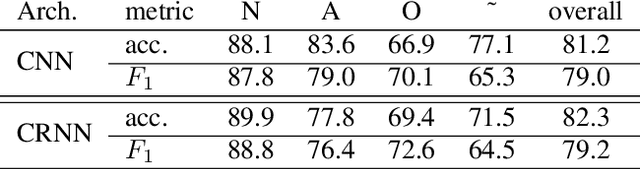
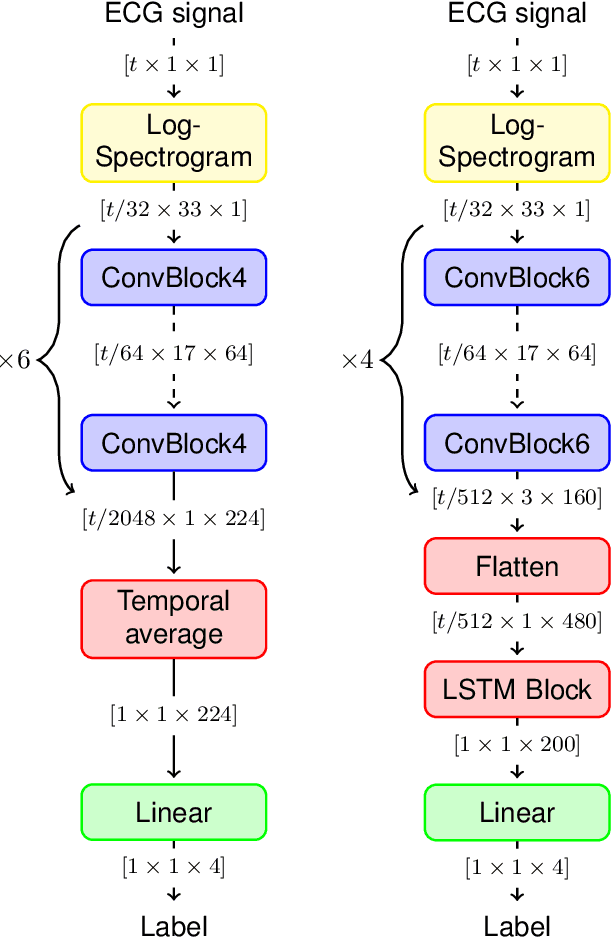
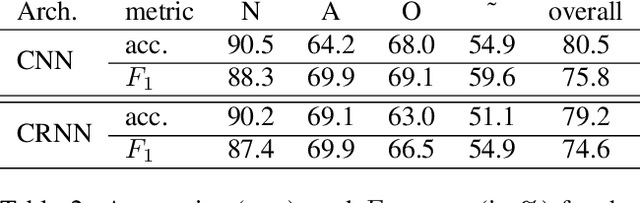
We propose two deep neural network architectures for classification of arbitrary-length electrocardiogram (ECG) recordings and evaluate them on the atrial fibrillation (AF) classification data set provided by the PhysioNet/CinC Challenge 2017. The first architecture is a deep convolutional neural network (CNN) with averaging-based feature aggregation across time. The second architecture combines convolutional layers for feature extraction with long-short term memory (LSTM) layers for temporal aggregation of features. As a key ingredient of our training procedure we introduce a simple data augmentation scheme for ECG data and demonstrate its effectiveness in the AF classification task at hand. The second architecture was found to outperform the first one, obtaining an $F_1$ score of $82.1$% on the hidden challenge testing set.

Towards Image Understanding from Deep Compression without Decoding

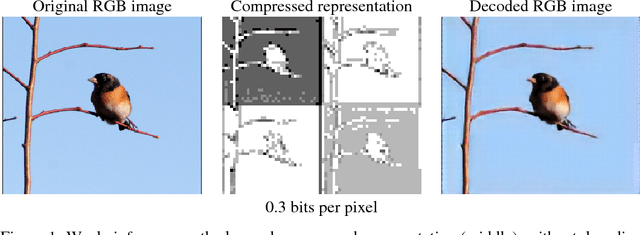
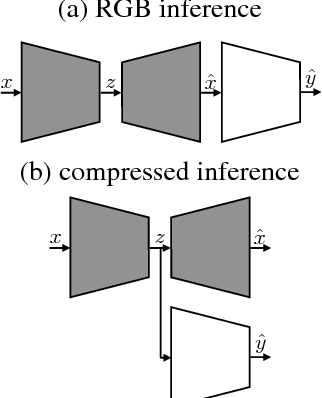
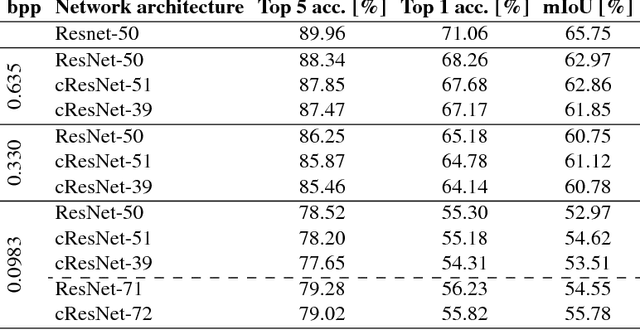
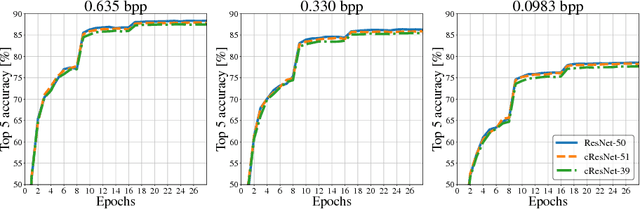
Motivated by recent work on deep neural network (DNN)-based image compression methods showing potential improvements in image quality, savings in storage, and bandwidth reduction, we propose to perform image understanding tasks such as classification and segmentation directly on the compressed representations produced by these compression methods. Since the encoders and decoders in DNN-based compression methods are neural networks with feature-maps as internal representations of the images, we directly integrate these with architectures for image understanding. This bypasses decoding of the compressed representation into RGB space and reduces computational cost. Our study shows that accuracies comparable to networks that operate on compressed RGB images can be achieved while reducing the computational complexity up to $2\times$. Furthermore, we show that synergies are obtained by jointly training compression networks with classification networks on the compressed representations, improving image quality, classification accuracy, and segmentation performance. We find that inference from compressed representations is particularly advantageous compared to inference from compressed RGB images for aggressive compression rates.

Greedy Algorithms for Cone Constrained Optimization with Convergence Guarantees

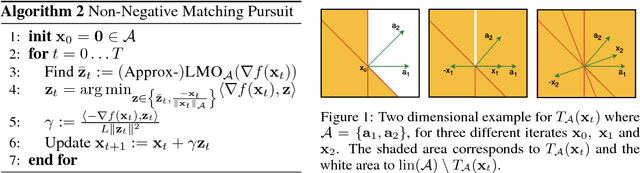
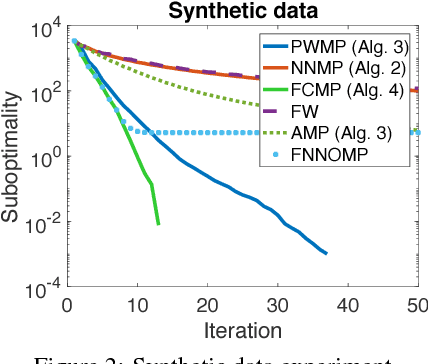
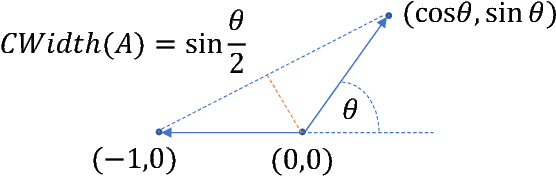
Greedy optimization methods such as Matching Pursuit (MP) and Frank-Wolfe (FW) algorithms regained popularity in recent years due to their simplicity, effectiveness and theoretical guarantees. MP and FW address optimization over the linear span and the convex hull of a set of atoms, respectively. In this paper, we consider the intermediate case of optimization over the convex cone, parametrized as the conic hull of a generic atom set, leading to the first principled definitions of non-negative MP algorithms for which we give explicit convergence rates and demonstrate excellent empirical performance. In particular, we derive sublinear ($\mathcal{O}(1/t)$) convergence on general smooth and convex objectives, and linear convergence ($\mathcal{O}(e^{-t})$) on strongly convex objectives, in both cases for general sets of atoms. Furthermore, we establish a clear correspondence of our algorithms to known algorithms from the MP and FW literature. Our novel algorithms and analyses target general atom sets and general objective functions, and hence are directly applicable to a large variety of learning settings.