Local Stochastic Gradient Descent Ascent: Convergence Analysis and Communication Efficiency

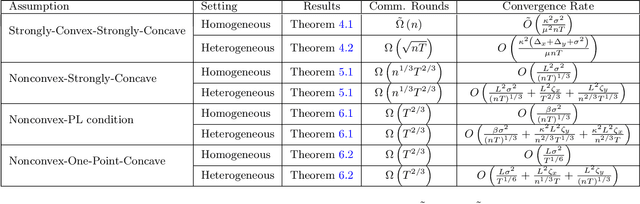
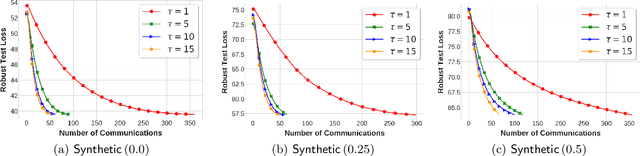
Local SGD is a promising approach to overcome the communication overhead in distributed learning by reducing the synchronization frequency among worker nodes. Despite the recent theoretical advances of local SGD in empirical risk minimization, the efficiency of its counterpart in minimax optimization remains unexplored. Motivated by large scale minimax learning problems, such as adversarial robust learning and training generative adversarial networks (GANs), we propose local Stochastic Gradient Descent Ascent (local SGDA), where the primal and dual variables can be trained locally and averaged periodically to significantly reduce the number of communications. We show that local SGDA can provably optimize distributed minimax problems in both homogeneous and heterogeneous data with reduced number of communications and establish convergence rates under strongly-convex-strongly-concave and nonconvex-strongly-concave settings. In addition, we propose a novel variant local SGDA+, to solve nonconvex-nonconcave problems. We give corroborating empirical evidence on different distributed minimax problems.

Distributionally Robust Federated Averaging

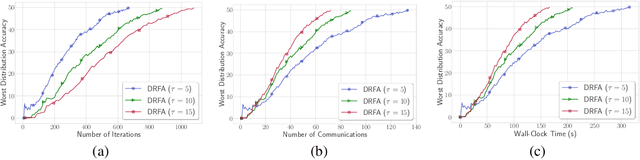
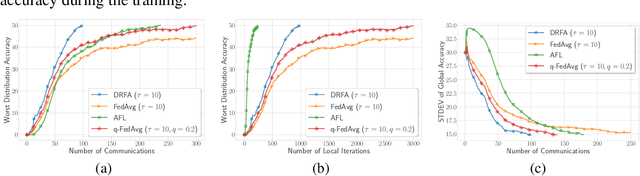
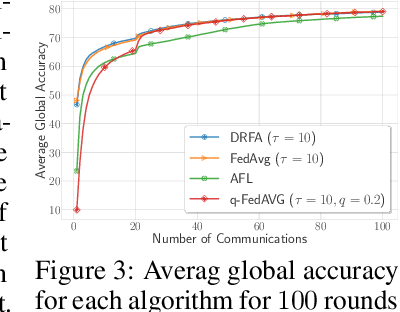
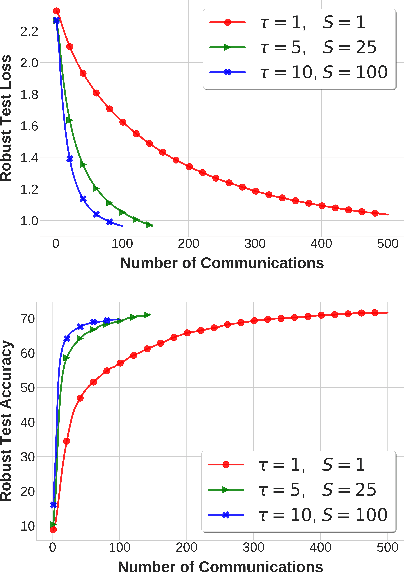
In this paper, we study communication efficient distributed algorithms for distributionally robust federated learning via periodic averaging with adaptive sampling. In contrast to standard empirical risk minimization, due to the minimax structure of the underlying optimization problem, a key difficulty arises from the fact that the global parameter that controls the mixture of local losses can only be updated infrequently on the global stage. To compensate for this, we propose a Distributionally Robust Federated Averaging (DRFA) algorithm that employs a novel snapshotting scheme to approximate the accumulation of history gradients of the mixing parameter. We analyze the convergence rate of DRFA in both convex-linear and nonconvex-linear settings. We also generalize the proposed idea to objectives with regularization on the mixture parameter and propose a proximal variant, dubbed as DRFA-Prox, with provable convergence rates. We also analyze an alternative optimization method for regularized cases in strongly-convex-strongly-concave and non-convex (under PL condition)-strongly-concave settings. To the best of our knowledge, this paper is the first to solve distributionally robust federated learning with reduced communication, and to analyze the efficiency of local descent methods on distributed minimax problems. We give corroborating experimental evidence for our theoretical results in federated learning settings.

Communication-efficient k-Means for Edge-based Machine Learning

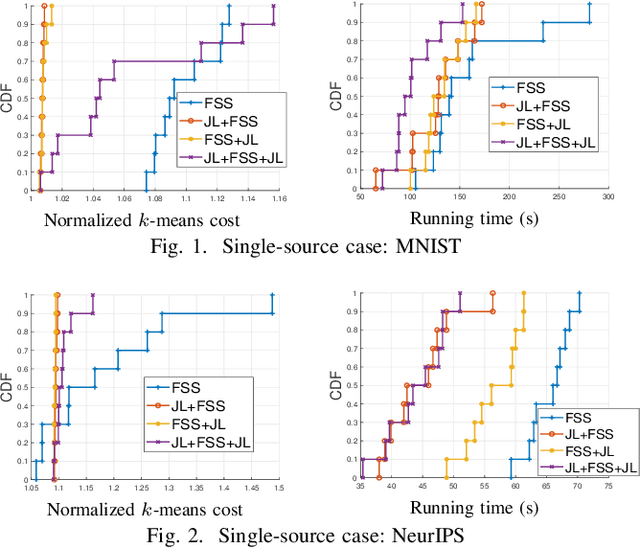
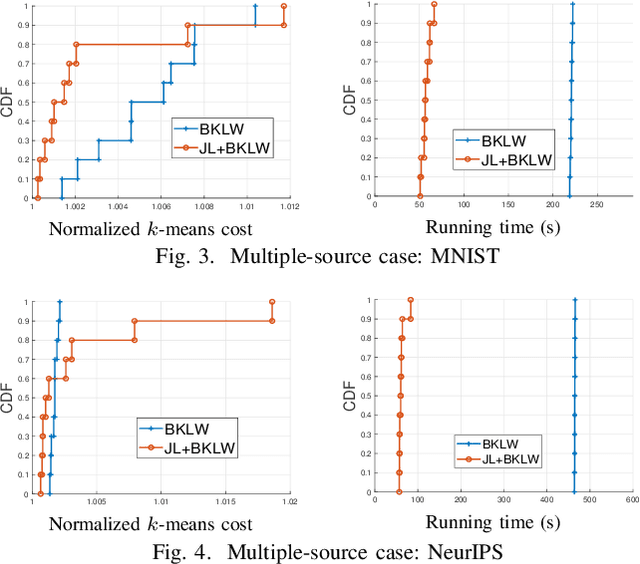
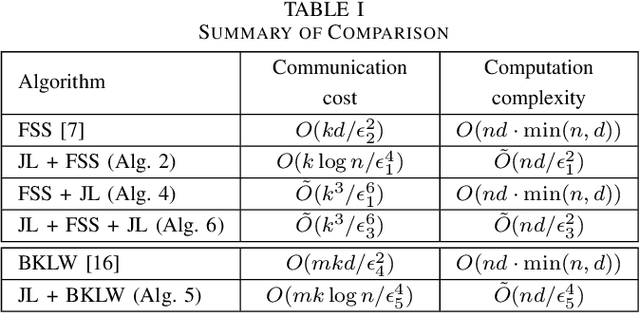
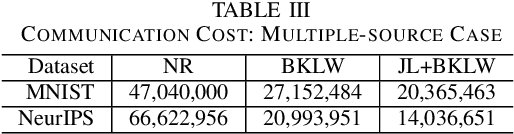
We consider the problem of computing the k-means centers for a large high-dimensional dataset in the context of edge-based machine learning, where data sources offload machine learning computation to nearby edge servers. k-Means computation is fundamental to many data analytics, and the capability of computing provably accurate k-means centers by leveraging the computation power of the edge servers, at a low communication and computation cost to the data sources, will greatly improve the performance of these analytics. We propose to let the data sources send small summaries, generated by joint dimensionality reduction (DR) and cardinality reduction (CR), to support approximate k-means computation at reduced complexity and communication cost. By analyzing the complexity, the communication cost, and the approximation error of k-means algorithms based on state-of-the-art DR/CR methods, we show that: (i) it is possible to achieve a near-optimal approximation at a near-linear complexity and a constant or logarithmic communication cost, (ii) the order of applying DR and CR significantly affects the complexity and the communication cost, and (iii) combining DR/CR methods with a properly configured quantizer can further reduce the communication cost without compromising the other performance metrics. Our findings are validated through experiments based on real datasets.

Online Structured Meta-learning

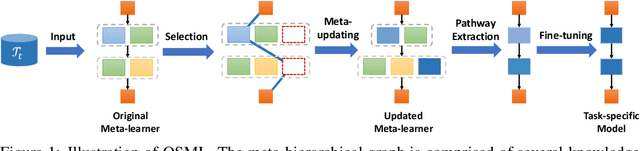
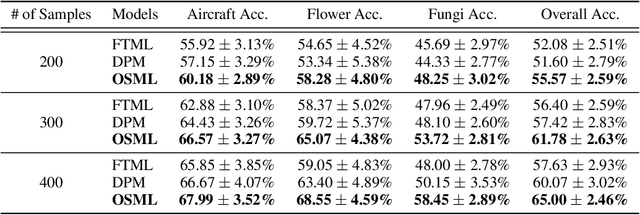
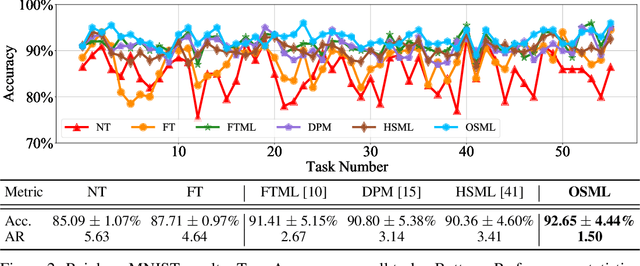
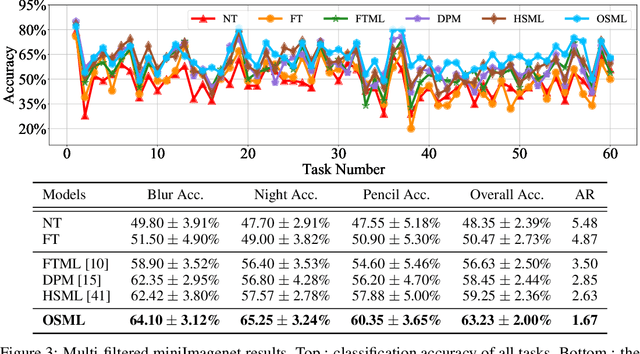
Learning quickly is of great importance for machine intelligence deployed in online platforms. With the capability of transferring knowledge from learned tasks, meta-learning has shown its effectiveness in online scenarios by continuously updating the model with the learned prior. However, current online meta-learning algorithms are limited to learn a globally-shared meta-learner, which may lead to sub-optimal results when the tasks contain heterogeneous information that are distinct by nature and difficult to share. We overcome this limitation by proposing an online structured meta-learning (OSML) framework. Inspired by the knowledge organization of human and hierarchical feature representation, OSML explicitly disentangles the meta-learner as a meta-hierarchical graph with different knowledge blocks. When a new task is encountered, it constructs a meta-knowledge pathway by either utilizing the most relevant knowledge blocks or exploring new blocks. Through the meta-knowledge pathway, the model is able to quickly adapt to the new task. In addition, new knowledge is further incorporated into the selected blocks. Experiments on three datasets demonstrate the effectiveness and interpretability of our proposed framework in the context of both homogeneous and heterogeneous tasks.

Federated Learning with Compression: Unified Analysis and Sharp Guarantees

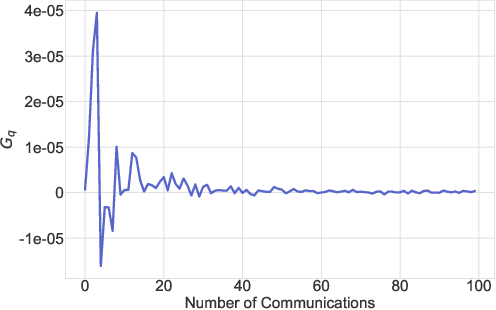
In federated learning, communication cost is often a critical bottleneck to scale up distributed optimization algorithms to collaboratively learn a model from millions of devices with potentially unreliable or limited communication and heterogeneous data distributions. Two notable trends to deal with the communication overhead of federated algorithms are \emph{gradient compression} and \emph{local computation with periodic communication}. Despite many attempts, characterizing the relationship between these two approaches has proven elusive. We address this by proposing a set of algorithms with periodical compressed (quantized or sparsified) communication and analyze their convergence properties in both homogeneous and heterogeneous local data distributions settings. For the homogeneous setting, our analysis improves existing bounds by providing tighter convergence rates for both \emph{strongly convex} and \emph{non-convex} objective functions. To mitigate data heterogeneity, we introduce a \emph{local gradient tracking} scheme and obtain sharp convergence rates that match the best-known communication complexities without compression for convex, strongly convex, and nonconvex settings. We complement our theoretical results and demonstrate the effectiveness of our proposed methods by several experiments on real-world datasets.

Minimal Variance Sampling with Provable Guarantees for Fast Training of Graph Neural Networks

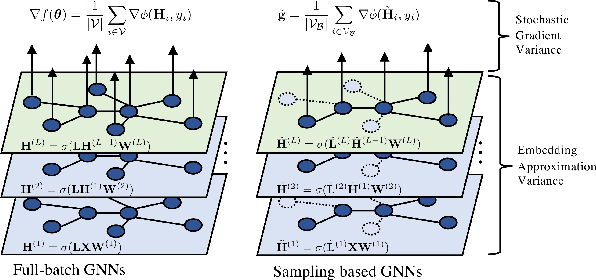
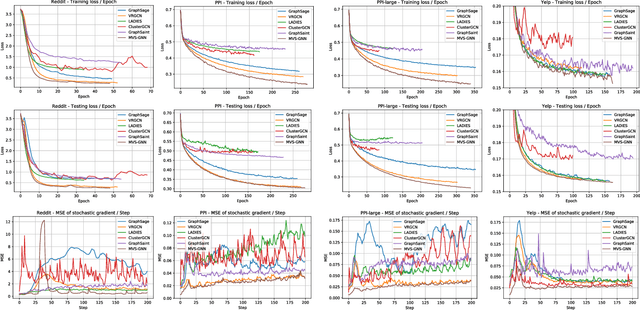
Sampling methods (e.g., node-wise, layer-wise, or subgraph) has become an indispensable strategy to speed up training large-scale Graph Neural Networks (GNNs). However, existing sampling methods are mostly based on the graph structural information and ignore the dynamicity of optimization, which leads to high variance in estimating the stochastic gradients. The high variance issue can be very pronounced in extremely large graphs, where it results in slow convergence and poor generalization. In this paper, we theoretically analyze the variance of sampling methods and show that, due to the composite structure of empirical risk, the variance of any sampling method can be decomposed into \textit{embedding approximation variance} in the forward stage and \textit{stochastic gradient variance} in the backward stage that necessities mitigating both types of variance to obtain faster convergence rate. We propose a decoupled variance reduction strategy that employs (approximate) gradient information to adaptively sample nodes with minimal variance, and explicitly reduces the variance introduced by embedding approximation. We show theoretically and empirically that the proposed method, even with smaller mini-batch sizes, enjoys a faster convergence rate and entails a better generalization compared to the existing methods.

Adaptive Personalized Federated Learning

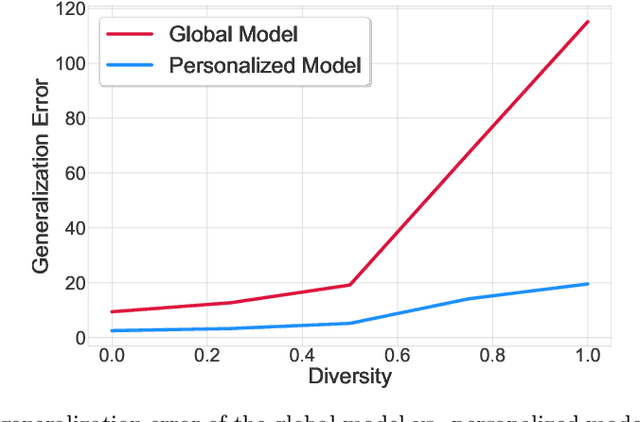
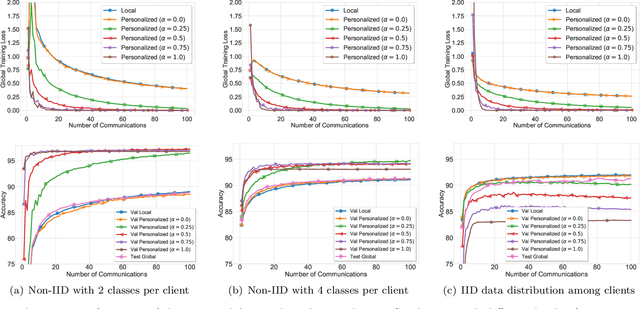
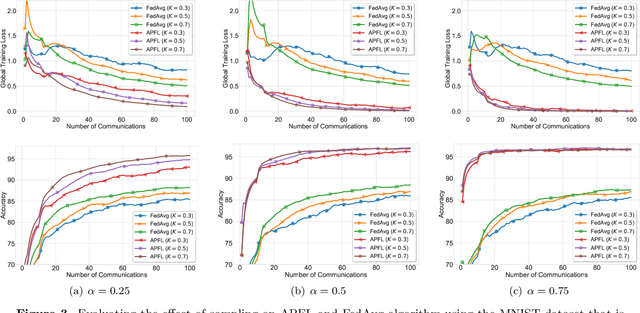
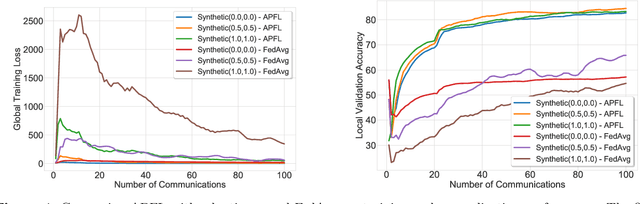
Investigation of the degree of personalization in federated learning algorithms has shown that only maximizing the performance of the global model will confine the capacity of the local models to personalize. In this paper, we advocate an adaptive personalized federated learning (APFL) algorithm, where each client will train their local models while contributing to the global model. Theoretically, we show that the mixture of local and global models can reduce the generalization error, using the multi-domain learning theory. We also propose a communication-reduced bilevel optimization method, which reduces the communication rounds to $O(\sqrt{T})$ and show that under strong convexity and smoothness assumptions, the proposed algorithm can achieve a convergence rate of $O(1/T)$ with some residual error. The residual error is related to the gradient diversity among local models, and the gap between optimal local and global models.

On the Convergence of Local Descent Methods in Federated Learning

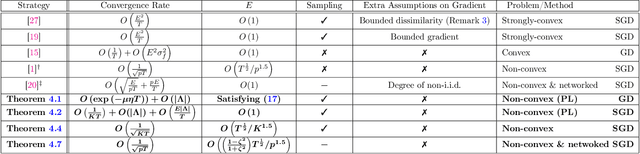
In federated distributed learning, the goal is to optimize a global training objective defined over distributed devices, where the data shard at each device is sampled from a possibly different distribution (a.k.a., heterogeneous or non i.i.d. data samples). In this paper, we generalize the local stochastic and full gradient descent with periodic averaging-- originally designed for homogeneous distributed optimization, to solve nonconvex optimization problems in federated learning. Although scant research is available on the effectiveness of local SGD in reducing the number of communication rounds in homogeneous setting, its convergence and communication complexity in heterogeneous setting is mostly demonstrated empirically and lacks through theoretical understating. To bridge this gap, we demonstrate that by properly analyzing the effect of unbiased gradients and sampling schema in federated setting, under mild assumptions, the implicit variance reduction feature of local distributed methods generalize to heterogeneous data shards and exhibits the best known convergence rates of homogeneous setting both in general nonconvex and under {\pl}~ condition (generalization of strong-convexity). Our theoretical results complement the recent empirical studies that demonstrate the applicability of local GD/SGD to federated learning. We also specialize the proposed local method for networked distributed optimization. To the best of our knowledge, the obtained convergence rates are the sharpest known to date on the convergence of local decant methods with periodic averaging for solving nonconvex federated optimization in both centralized and networked distributed optimization.

Efficient Fair Principal Component Analysis

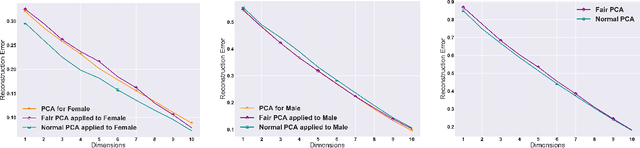
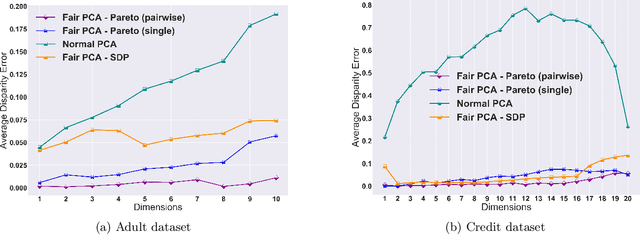
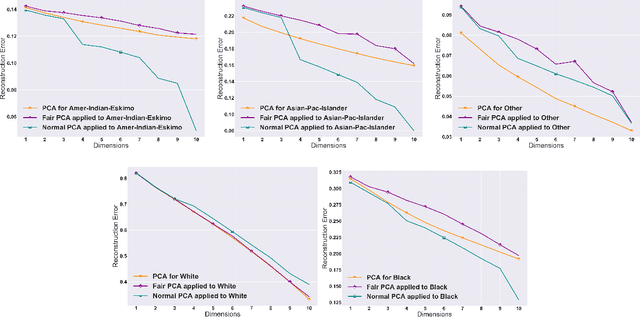
The flourishing assessments of fairness measure in machine learning algorithms have shown that dimension reduction methods such as PCA treat data from different sensitive groups unfairly. In particular, by aggregating data of different groups, the reconstruction error of the learned subspace becomes biased towards some populations that might hurt or benefit those groups inherently, leading to an unfair representation. On the other hand, alleviating the bias to protect sensitive groups in learning the optimal projection, would lead to a higher reconstruction error overall. This introduces a trade-off between sensitive groups' sacrifices and benefits, and the overall reconstruction error. In this paper, in pursuit of achieving fairness criteria in PCA, we introduce a more efficient notion of Pareto fairness, cast the Pareto fair dimensionality reduction as a multi-objective optimization problem, and propose an adaptive gradient-based algorithm to solve it. Using the notion of Pareto optimality, we can guarantee that the solution of our proposed algorithm belongs to the Pareto frontier for all groups, which achieves the optimal trade-off between those aforementioned conflicting objectives. This framework can be efficiently generalized to multiple group sensitive features, as well. We provide convergence analysis of our algorithm for both convex and non-convex objectives and show its efficacy through empirical studies on different datasets, in comparison with the state-of-the-art algorithm.

Local SGD with Periodic Averaging: Tighter Analysis and Adaptive Synchronization

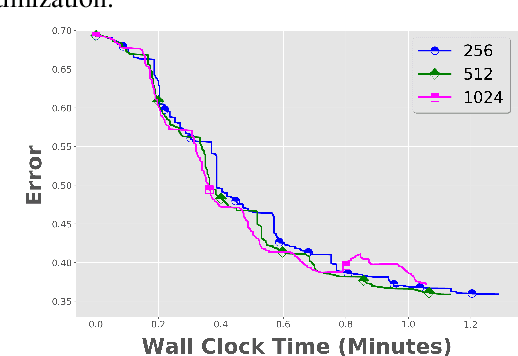
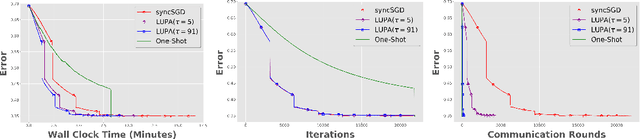
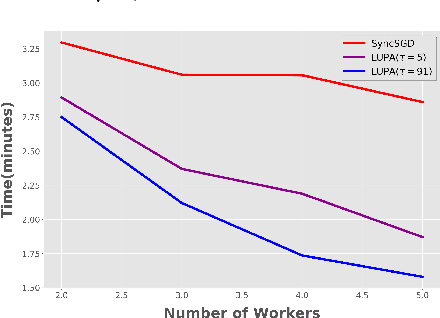
Communication overhead is one of the key challenges that hinders the scalability of distributed optimization algorithms. In this paper, we study local distributed SGD, where data is partitioned among computation nodes, and the computation nodes perform local updates with periodically exchanging the model among the workers to perform averaging. While local SGD is empirically shown to provide promising results, a theoretical understanding of its performance remains open. We strengthen convergence analysis for local SGD, and show that local SGD can be far less expensive and applied far more generally than current theory suggests. Specifically, we show that for loss functions that satisfy the Polyak-{\L}ojasiewicz condition, $O((pT)^{1/3})$ rounds of communication suffice to achieve a linear speed up, that is, an error of $O(1/pT)$, where $T$ is the total number of model updates at each worker. This is in contrast with previous work which required higher number of communication rounds, as well as was limited to strongly convex loss functions, for a similar asymptotic performance. We also develop an adaptive synchronization scheme that provides a general condition for linear speed up. Finally, we validate the theory with experimental results, running over AWS EC2 clouds and an internal GPU cluster.