Fair Exploration and Exploitation

In this paper we consider the contextual bandit problem with a finite (or infinite and clustered) context set. We consider the fully adversarial problem in which, apart from having bounded losses, there are no assumptions whatsoever on the generation of the contexts and losses. In our problem we assume that the context set is partitioned into a set of protected groups. At the start of each trial we are given a probability distribution over the context set and are required (on that trial) to be fair with respect to that distribution, in that if the context (for that trial) was drawn from the distribution then our choice of action would be unbiased towards any protected group. We develop an algorithm FexEx for this problem which has remarkable efficiency, having a space and per-trial time complexity at most linear in the dimensionality of the policy space. FexEx can handle non-stationarity, in that its regret can be bounded with respect to any sequence of policies satisfying the fairness constraints. For such a sequence the regret bound of FexEx is essentially the same as that of running Exp3.S for each context independently (an approach that does not satisfy the fairness constraints).

Online Convex Optimisation: The Optimal Switching Regret for all Segmentations Simultaneously

We consider the classic problem of online convex optimisation. Whereas the notion of static regret is relevant for stationary problems, the notion of switching regret is more appropriate for non-stationary problems. A switching regret is defined relative to any segmentation of the trial sequence, and is equal to the sum of the static regrets of each segment. In this paper we show that, perhaps surprisingly, we can achieve the asymptotically optimal switching regret on every possible segmentation simultaneously. Our algorithm for doing so is very efficient: having a space and per-trial time complexity that is logarithmic in the time-horizon. Our algorithm also obtains novel bounds on its dynamic regret: being adaptive to variations in the rate of change of the comparator sequence.

Fusion Encoder Networks

In this paper we present fusion encoder networks (FENs): a class of algorithms for creating neural networks that map sequences to outputs. The resulting neural network has only logarithmic depth (alleviating the degradation of data as it propagates through the network) and can process sequences in linear time (or in logarithmic time with a linear number of processors). The crucial property of FENs is that they learn by training a quasi-linear number of constant-depth feed-forward neural networks in parallel. The fact that these networks have constant depth means that backpropagation works well. We note that currently the performance of FENs is only conjectured as we are yet to implement them.

Bandits with Abstention under Expert Advice

We study the classic problem of prediction with expert advice under bandit feedback. Our model assumes that one action, corresponding to the learner's abstention from play, has no reward or loss on every trial. We propose the CBA algorithm, which exploits this assumption to obtain reward bounds that can significantly improve those of the classical Exp4 algorithm. We can view our problem as the aggregation of confidence-rated predictors when the learner has the option of abstention from play. Importantly, we are the first to achieve bounds on the expected cumulative reward for general confidence-rated predictors. In the special case of specialists we achieve a novel reward bound, significantly improving previous bounds of SpecialistExp (treating abstention as another action). As an example application, we discuss learning unions of balls in a finite metric space. In this contextual setting, we devise an efficient implementation of CBA, reducing the runtime from quadratic to almost linear in the number of contexts. Preliminary experiments show that CBA improves over existing bandit algorithms.

A Hierarchical Nearest Neighbour Approach to Contextual Bandits

In this paper we consider the adversarial contextual bandit problem in metric spaces. The paper "Nearest neighbour with bandit feedback" tackled this problem but when there are many contexts near the decision boundary of the comparator policy it suffers from a high regret. In this paper we eradicate this problem, designing an algorithm in which we can hold out any set of contexts when computing our regret term. Our algorithm builds on that of "Nearest neighbour with bandit feedback" and hence inherits its extreme computational efficiency.

Sum-max Submodular Bandits

Many online decision-making problems correspond to maximizing a sequence of submodular functions. In this work, we introduce sum-max functions, a subclass of monotone submodular functions capturing several interesting problems, including best-of-$K$-bandits, combinatorial bandits, and the bandit versions on facility location, $M$-medians, and hitting sets. We show that all functions in this class satisfy a key property that we call pseudo-concavity. This allows us to prove $\big(1 - \frac{1}{e}\big)$-regret bounds for bandit feedback in the nonstochastic setting of the order of $\sqrt{MKT}$ (ignoring log factors), where $T$ is the time horizon and $M$ is a cardinality constraint. This bound, attained by a simple and efficient algorithm, significantly improves on the $\widetilde{O}\big(T^{2/3}\big)$ regret bound for online monotone submodular maximization with bandit feedback.

Nearest Neighbour with Bandit Feedback

In this paper we adapt the nearest neighbour rule to the contextual bandit problem. Our algorithm handles the fully adversarial setting in which no assumptions at all are made about the data-generation process. When combined with a sufficiently fast data-structure for (perhaps approximate) adaptive nearest neighbour search, such as a navigating net, our algorithm is extremely efficient - having a per trial running time polylogarithmic in both the number of trials and actions, and taking only quasi-linear space.

Regret Guarantees for Adversarial Online Collaborative Filtering

We investigate the problem of online collaborative filtering under no-repetition constraints, whereby users need to be served content in an online fashion and a given user cannot be recommended the same content item more than once. We design and analyze a fully adaptive algorithm that works under biclustering assumptions on the user-item preference matrix, and show that this algorithm exhibits an optimal regret guarantee, while being oblivious to any prior knowledge about the sequence of users, the universe of items, as well as the biclustering parameters of the preference matrix. We further propose a more robust version of the algorithm which addresses the scenario when the preference matrix is adversarially perturbed. We then give regret guarantees that scale with the amount by which the preference matrix is perturbed from a biclustered structure. To our knowledge, these are the first results on online collaborative filtering that hold at this level of generality and adaptivity under no-repetition constraints.

Joint Coreset Construction and Quantization for Distributed Machine Learning

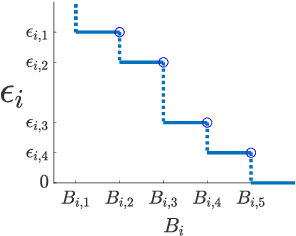
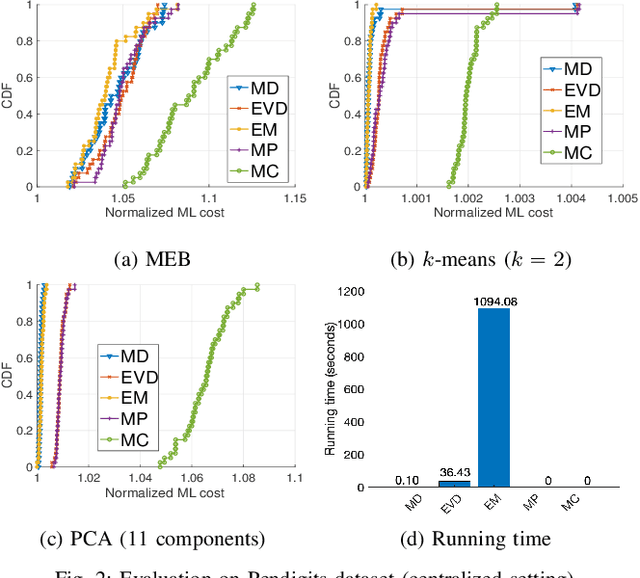
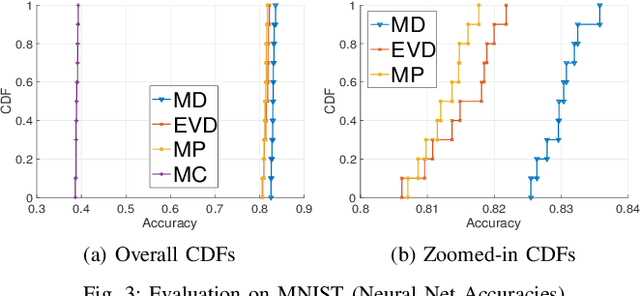
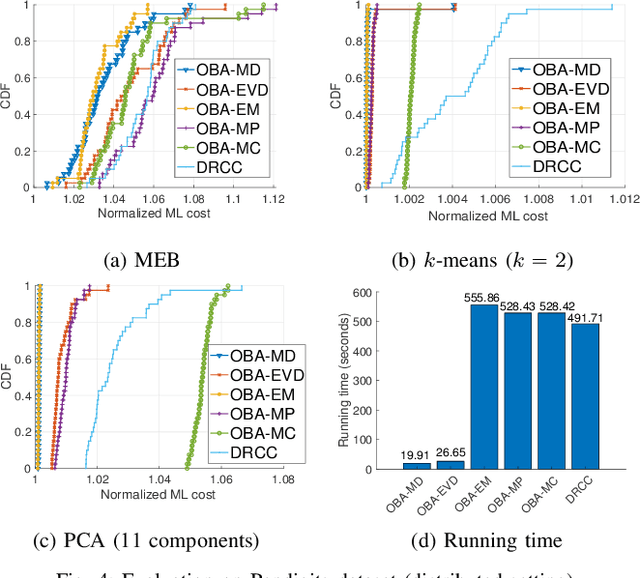
Coresets are small, weighted summaries of larger datasets, aiming at providing provable error bounds for machine learning (ML) tasks while significantly reducing the communication and computation costs. To achieve a better trade-off between ML error bounds and costs, we propose the first framework to incorporate quantization techniques into the process of coreset construction. Specifically, we theoretically analyze the ML error bounds caused by a combination of coreset construction and quantization. Based on that, we formulate an optimization problem to minimize the ML error under a fixed budget of communication cost. To improve the scalability for large datasets, we identify two proxies of the original objective function, for which efficient algorithms are developed. For the case of data on multiple nodes, we further design a novel algorithm to allocate the communication budget to the nodes while minimizing the overall ML error. Through extensive experiments on multiple real-world datasets, we demonstrate the effectiveness and efficiency of our proposed algorithms for a variety of ML tasks. In particular, our algorithms have achieved more than 90% data reduction with less than 10% degradation in ML performance in most cases.

Communication-efficient k-Means for Edge-based Machine Learning

We consider the problem of computing the k-means centers for a large high-dimensional dataset in the context of edge-based machine learning, where data sources offload machine learning computation to nearby edge servers. k-Means computation is fundamental to many data analytics, and the capability of computing provably accurate k-means centers by leveraging the computation power of the edge servers, at a low communication and computation cost to the data sources, will greatly improve the performance of these analytics. We propose to let the data sources send small summaries, generated by joint dimensionality reduction (DR) and cardinality reduction (CR), to support approximate k-means computation at reduced complexity and communication cost. By analyzing the complexity, the communication cost, and the approximation error of k-means algorithms based on state-of-the-art DR/CR methods, we show that: (i) it is possible to achieve a near-optimal approximation at a near-linear complexity and a constant or logarithmic communication cost, (ii) the order of applying DR and CR significantly affects the complexity and the communication cost, and (iii) combining DR/CR methods with a properly configured quantizer can further reduce the communication cost without compromising the other performance metrics. Our findings are validated through experiments based on real datasets.