Gradient Descent Converges Linearly for Logistic Regression on Separable Data

We show that running gradient descent with variable learning rate guarantees loss $f(x) \leq 1.1 \cdot f(x^*) + \epsilon$ for the logistic regression objective, where the error $\epsilon$ decays exponentially with the number of iterations and polynomially with the magnitude of the entries of an arbitrary fixed solution $x^*$. This is in contrast to the common intuition that the absence of strong convexity precludes linear convergence of first-order methods, and highlights the importance of variable learning rates for gradient descent. We also apply our ideas to sparse logistic regression, where they lead to an exponential improvement of the sparsity-error tradeoff.

Iterative Hard Thresholding with Adaptive Regularization: Sparser Solutions Without Sacrificing Runtime

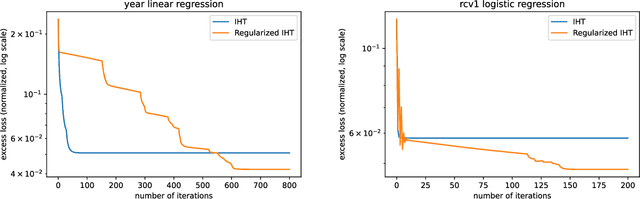
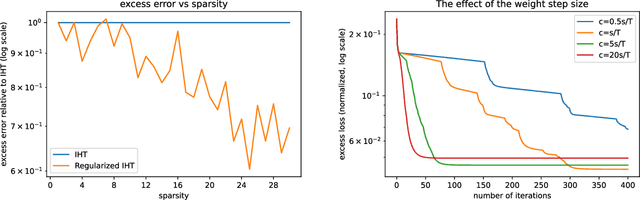
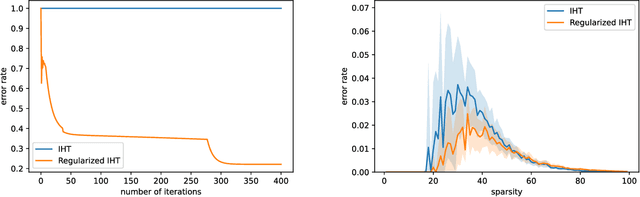
We propose a simple modification to the iterative hard thresholding (IHT) algorithm, which recovers asymptotically sparser solutions as a function of the condition number. When aiming to minimize a convex function $f(x)$ with condition number $\kappa$ subject to $x$ being an $s$-sparse vector, the standard IHT guarantee is a solution with relaxed sparsity $O(s\kappa^2)$, while our proposed algorithm, regularized IHT, returns a solution with sparsity $O(s\kappa)$. Our algorithm significantly improves over ARHT which also finds a solution of sparsity $O(s\kappa)$, as it does not require re-optimization in each iteration (and so is much faster), is deterministic, and does not require knowledge of the optimal solution value $f(x^*)$ or the optimal sparsity level $s$. Our main technical tool is an adaptive regularization framework, in which the algorithm progressively learns the weights of an $\ell_2$ regularization term that will allow convergence to sparser solutions. We also apply this framework to low rank optimization, where we achieve a similar improvement of the best known condition number dependence from $\kappa^2$ to $\kappa$.

TSI: an Ad Text Strength Indicator using Text-to-CTR and Semantic-Ad-Similarity

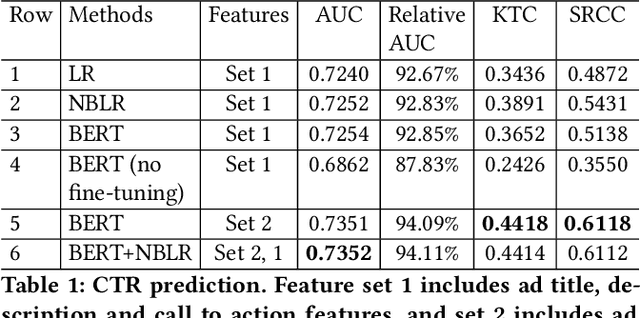
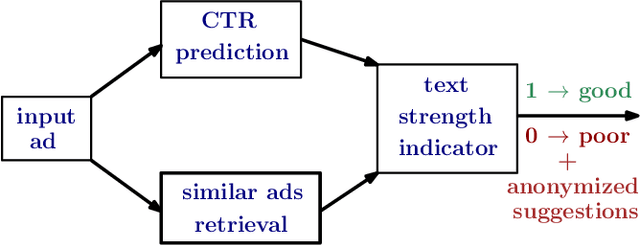
Coming up with effective ad text is a time consuming process, and particularly challenging for small businesses with limited advertising experience. When an inexperienced advertiser onboards with a poorly written ad text, the ad platform has the opportunity to detect low performing ad text, and provide improvement suggestions. To realize this opportunity, we propose an ad text strength indicator (TSI) which: (i) predicts the click-through-rate (CTR) for an input ad text, (ii) fetches similar existing ads to create a neighborhood around the input ad, (iii) and compares the predicted CTRs in the neighborhood to declare whether the input ad is strong or weak. In addition, as suggestions for ad text improvement, TSI shows anonymized versions of superior ads (higher predicted CTR) in the neighborhood. For (i), we propose a BERT based text-to-CTR model trained on impressions and clicks associated with an ad text. For (ii), we propose a sentence-BERT based semantic-ad-similarity model trained using weak labels from ad campaign setup data. Offline experiments demonstrate that our BERT based text-to-CTR model achieves a significant lift in CTR prediction AUC for cold start (new) advertisers compared to bag-of-words based baselines. In addition, our semantic-textual-similarity model for similar ads retrieval achieves a precision@1 of 0.93 (for retrieving ads from the same product category); this is significantly higher compared to unsupervised TF-IDF, word2vec, and sentence-BERT baselines. Finally, we share promising online results from advertisers in the Yahoo (Verizon Media) ad platform where a variant of TSI was implemented with sub-second end-to-end latency.

VisualTextRank: Unsupervised Graph-based Content Extraction for Automating Ad Text to Image Search

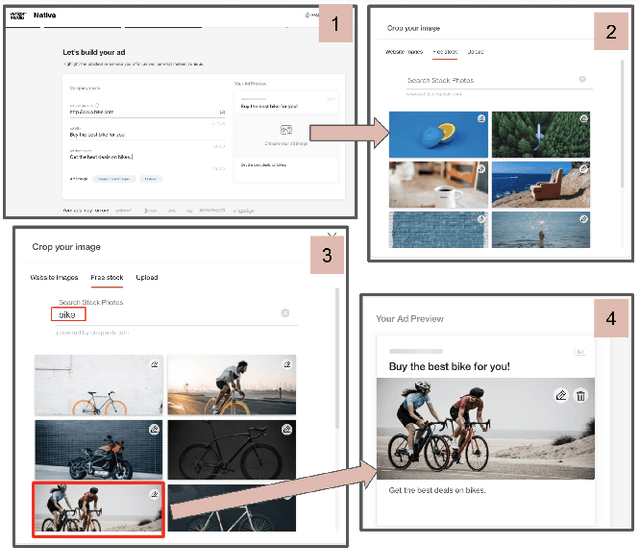
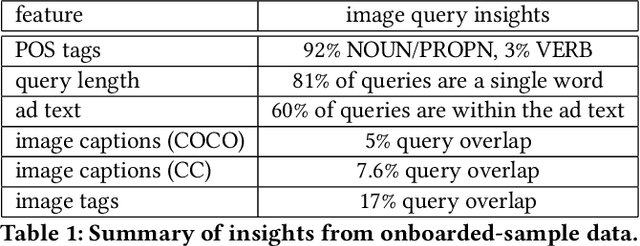
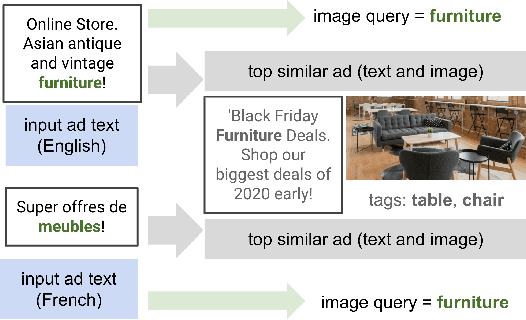
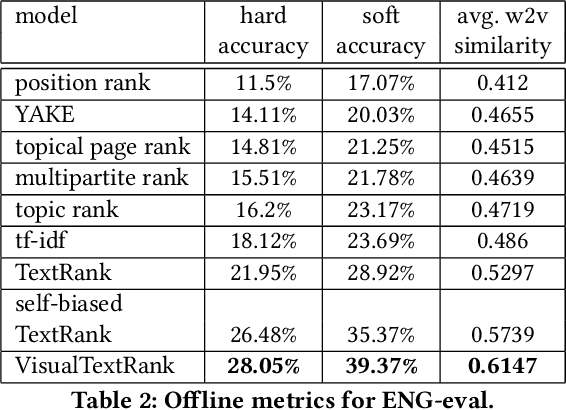
Numerous online stock image libraries offer high quality yet copyright free images for use in marketing campaigns. To assist advertisers in navigating such third party libraries, we study the problem of automatically fetching relevant ad images given the ad text (via a short textual query for images). Motivated by our observations in logged data on ad image search queries (given ad text), we formulate a keyword extraction problem, where a keyword extracted from the ad text (or its augmented version) serves as the ad image query. In this context, we propose VisualTextRank: an unsupervised method to (i) augment input ad text using semantically similar ads, and (ii) extract the image query from the augmented ad text. VisualTextRank builds on prior work on graph based context extraction (biased TextRank in particular) by leveraging both the text and image of similar ads for better keyword extraction, and using advertiser category specific biasing with sentence-BERT embeddings. Using data collected from the Verizon Media Native (Yahoo Gemini) ad platform's stock image search feature for onboarding advertisers, we demonstrate the superiority of VisualTextRank compared to competitive keyword extraction baselines (including an $11\%$ accuracy lift over biased TextRank). For the case when the stock image library is restricted to English queries, we show the effectiveness of VisualTextRank on multilingual ads (translated to English) while leveraging semantically similar English ads. Online tests with a simplified version of VisualTextRank led to a 28.7% increase in the usage of stock image search, and a 41.6% increase in the advertiser onboarding rate in the Verizon Media Native ad platform.

Local Search Algorithms for Rank-Constrained Convex Optimization

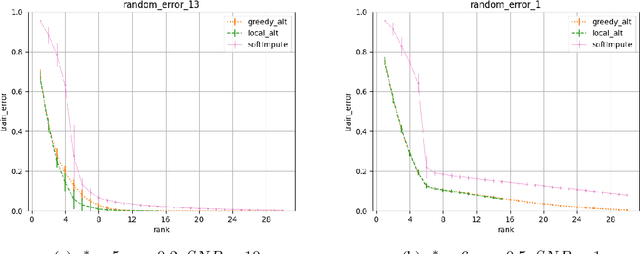
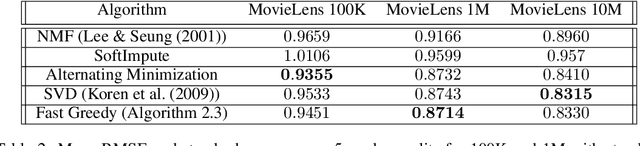
We propose greedy and local search algorithms for rank-constrained convex optimization, namely solving $\underset{\mathrm{rank}(A)\leq r^*}{\min}\, R(A)$ given a convex function $R:\mathbb{R}^{m\times n}\rightarrow \mathbb{R}$ and a parameter $r^*$. These algorithms consist of repeating two steps: (a) adding a new rank-1 matrix to $A$ and (b) enforcing the rank constraint on $A$. We refine and improve the theoretical analysis of Shalev-Shwartz et al. (2011), and show that if the rank-restricted condition number of $R$ is $\kappa$, a solution $A$ with rank $O(r^*\cdot \min\{\kappa \log \frac{R(\mathbf{0})-R(A^*)}{\epsilon}, \kappa^2\})$ and $R(A) \leq R(A^*) + \epsilon$ can be recovered, where $A^*$ is the optimal solution. This significantly generalizes associated results on sparse convex optimization, as well as rank-constrained convex optimization for smooth functions. We then introduce new practical variants of these algorithms that have superior runtime and recover better solutions in practice. We demonstrate the versatility of these methods on a wide range of applications involving matrix completion and robust principal component analysis.

Sparse Convex Optimization via Adaptively Regularized Hard Thresholding

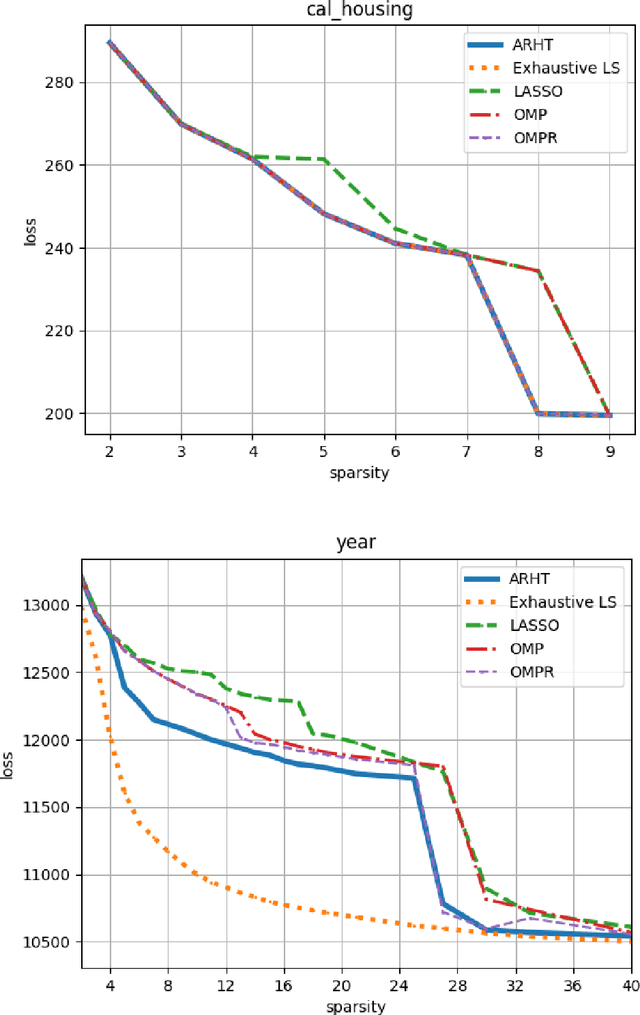
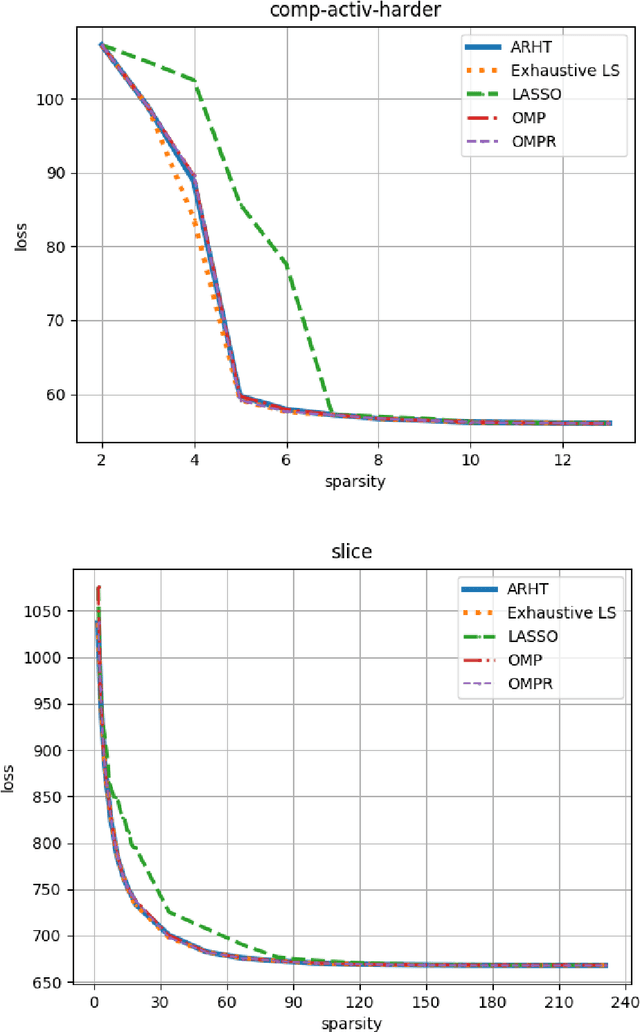
The goal of Sparse Convex Optimization is to optimize a convex function $f$ under a sparsity constraint $s\leq s^*\gamma$, where $s^*$ is the target number of non-zero entries in a feasible solution (sparsity) and $\gamma\geq 1$ is an approximation factor. There has been a lot of work to analyze the sparsity guarantees of various algorithms (LASSO, Orthogonal Matching Pursuit (OMP), Iterative Hard Thresholding (IHT)) in terms of the Restricted Condition Number $\kappa$. The best known algorithms guarantee to find an approximate solution of value $f(x^*)+\epsilon$ with the sparsity bound of $\gamma = O\left(\kappa\min\left\{\log \frac{f(x^0)-f(x^*)}{\epsilon}, \kappa\right\}\right)$, where $x^*$ is the target solution. We present a new Adaptively Regularized Hard Thresholding (ARHT) algorithm that makes significant progress on this problem by bringing the bound down to $\gamma=O(\kappa)$, which has been shown to be tight for a general class of algorithms including LASSO, OMP, and IHT. This is achieved without significant sacrifice in the runtime efficiency compared to the fastest known algorithms. We also provide a new analysis of OMP with Replacement (OMPR) for general $f$, under the condition $s > s^* \frac{\kappa^2}{4}$, which yields Compressed Sensing bounds under the Restricted Isometry Property (RIP). When compared to other Compressed Sensing approaches, it has the advantage of providing a strong tradeoff between the RIP condition and the solution sparsity, while working for any general function $f$ that meets the RIP condition.

On the computational complexity of the probabilistic label tree algorithms

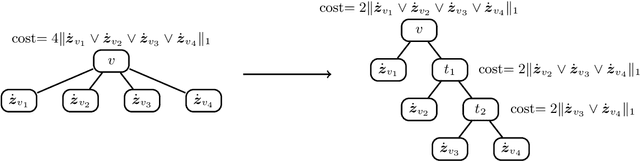
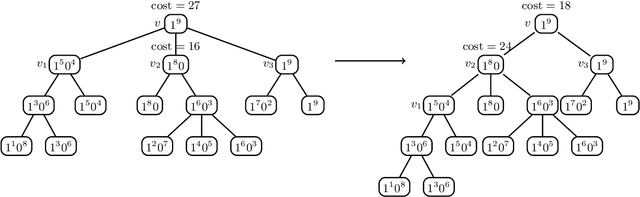
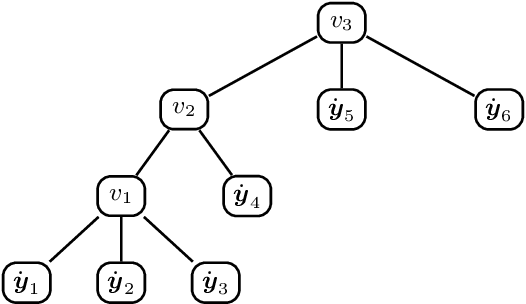
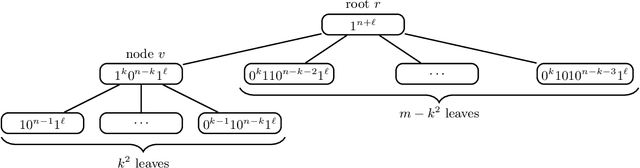
Label tree-based algorithms are widely used to tackle multi-class and multi-label problems with a large number of labels. We focus on a particular subclass of these algorithms that use probabilistic classifiers in the tree nodes. Examples of such algorithms are hierarchical softmax (HSM), designed for multi-class classification, and probabilistic label trees (PLTs) that generalize HSM to multi-label problems. If the tree structure is given, learning of PLT can be solved with provable regret guaranties [Wydmuch et.al. 2018]. However, to find a tree structure that results in a PLT with a low training and prediction computational costs as well as low statistical error seems to be a very challenging problem, not well-understood yet. In this paper, we address the problem of finding a tree structure that has low computational cost. First, we show that finding a tree with optimal training cost is NP-complete, nevertheless there are some tractable special cases with either perfect approximation or exact solution that can be obtained in linear time in terms of the number of labels $m$. For the general case, we obtain $O(\log m)$ approximation in linear time too. Moreover, we prove an upper bound on the expected prediction cost expressed in terms of the expected training cost. We also show that under additional assumptions the prediction cost of a PLT is $O(\log m)$.

An Algorithm for Online K-Means Clustering

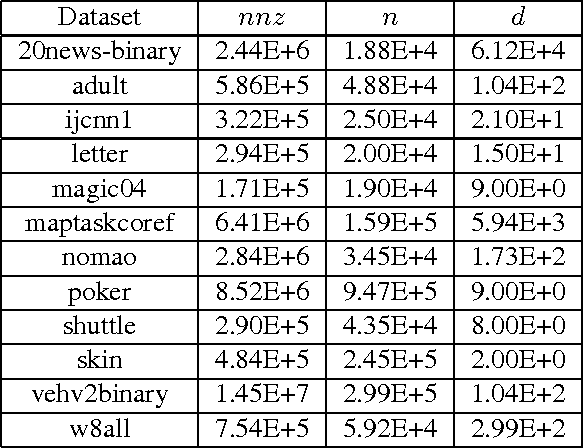
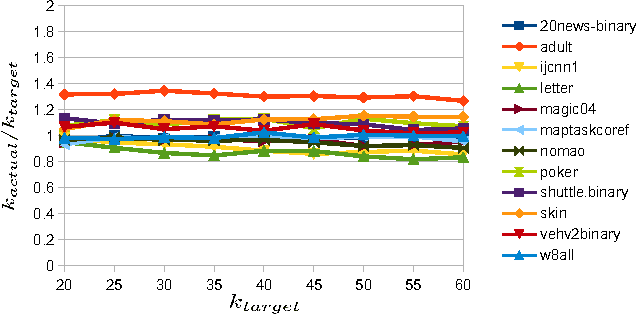
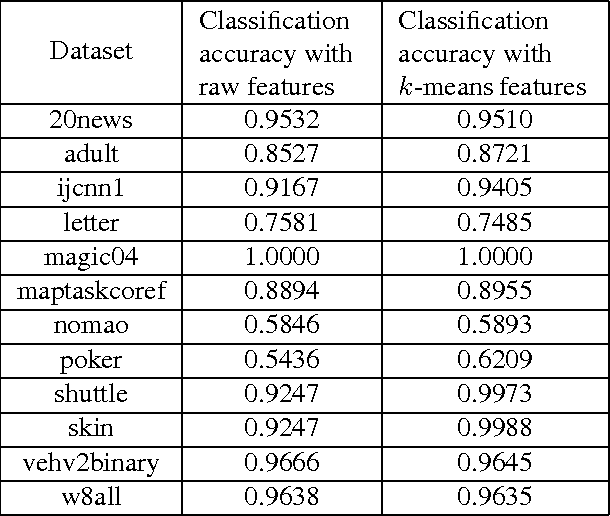
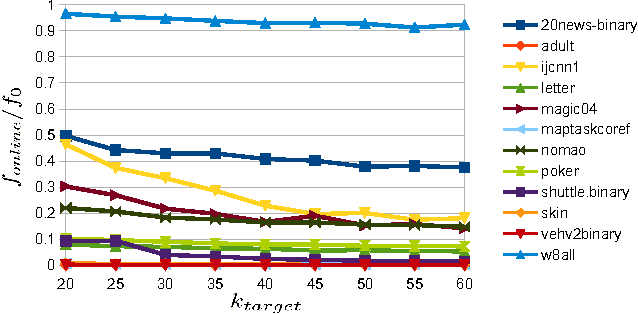
This paper shows that one can be competitive with the k-means objective while operating online. In this model, the algorithm receives vectors v_1,...,v_n one by one in an arbitrary order. For each vector the algorithm outputs a cluster identifier before receiving the next one. Our online algorithm generates ~O(k) clusters whose k-means cost is ~O(W*). Here, W* is the optimal k-means cost using k clusters and ~O suppresses poly-logarithmic factors. We also show that, experimentally, it is not much worse than k-means++ while operating in a strictly more constrained computational model.