Local Search Algorithms for Rank-Constrained Convex Optimization
Paper and Code
Jan 15, 2021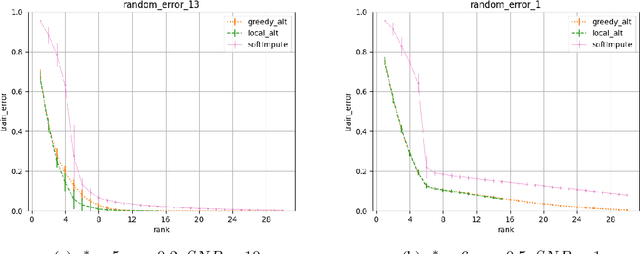


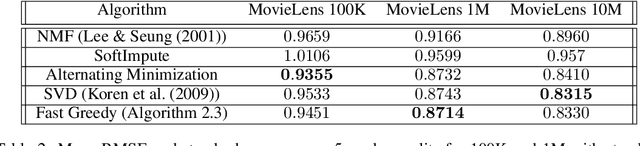
We propose greedy and local search algorithms for rank-constrained convex optimization, namely solving $\underset{\mathrm{rank}(A)\leq r^*}{\min}\, R(A)$ given a convex function $R:\mathbb{R}^{m\times n}\rightarrow \mathbb{R}$ and a parameter $r^*$. These algorithms consist of repeating two steps: (a) adding a new rank-1 matrix to $A$ and (b) enforcing the rank constraint on $A$. We refine and improve the theoretical analysis of Shalev-Shwartz et al. (2011), and show that if the rank-restricted condition number of $R$ is $\kappa$, a solution $A$ with rank $O(r^*\cdot \min\{\kappa \log \frac{R(\mathbf{0})-R(A^*)}{\epsilon}, \kappa^2\})$ and $R(A) \leq R(A^*) + \epsilon$ can be recovered, where $A^*$ is the optimal solution. This significantly generalizes associated results on sparse convex optimization, as well as rank-constrained convex optimization for smooth functions. We then introduce new practical variants of these algorithms that have superior runtime and recover better solutions in practice. We demonstrate the versatility of these methods on a wide range of applications involving matrix completion and robust principal component analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge