Towards Optimal Beacon Placement for Range-Aided Localization

Range-based localization is ubiquitous: global navigation satellite systems (GNSS) power mobile phone-based navigation, and autonomous mobile robots can use range measurements from a variety of modalities including sonar, radar, and even WiFi signals. Many of these localization systems rely on fixed anchors or beacons with known positions acting as transmitters or receivers. In this work, we answer a fundamental question: given a set of positions we would like to localize, how should beacons be placed so as to minimize localization error? Specifically, we present an information theoretic method for optimally selecting an arrangement consisting of a few beacons from a large set of candidate positions. By formulating localization as maximum a posteriori (MAP) estimation, we can cast beacon arrangement as a submodular set function maximization problem. This approach is probabilistically rigorous, simple to implement, and extremely flexible. Furthermore, we prove that the submodular structure of our problem formulation ensures that a greedy algorithm for beacon arrangement has suboptimality guarantees. We compare our method with a number of benchmarks on simulated data and release an open source Python implementation of our algorithm and experiments.

OASIS: Optimal Arrangements for Sensing in SLAM

The number and arrangement of sensors on an autonomous mobile robot dramatically influence its perception capabilities. Ensuring that sensors are mounted in a manner that enables accurate detection, localization, and mapping is essential for the success of downstream control tasks. However, when designing a new robotic platform, researchers and practitioners alike usually mimic standard configurations or maximize simple heuristics like field-of-view (FOV) coverage to decide where to place exteroceptive sensors. In this work, we conduct an information-theoretic investigation of this overlooked element of mobile robotic perception in the context of simultaneous localization and mapping (SLAM). We show how to formalize the sensor arrangement problem as a form of subset selection under the E-optimality performance criterion. While this formulation is NP-hard in general, we further show that a combination of greedy sensor selection and fast convex relaxation-based post-hoc verification enables the efficient recovery of certifiably optimal sensor designs in practice. Results from synthetic experiments reveal that sensors placed with OASIS outperform benchmarks in terms of mean squared error of visual SLAM estimates.

Euclidean Equivariant Models for Generative Graphical Inverse Kinematics

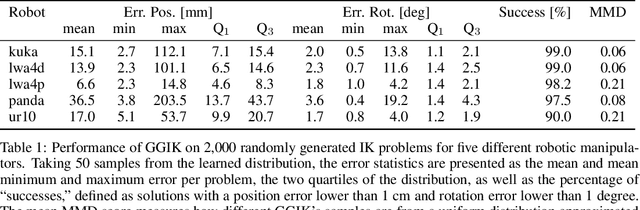
Quickly and reliably finding accurate inverse kinematics (IK) solutions remains a challenging problem for robotic manipulation. Existing numerical solvers typically produce a single solution only and rely on local search techniques to minimize a highly nonconvex objective function. Recently, learning-based approaches that approximate the entire feasible set of solutions have shown promise as a means to generate multiple fast and accurate IK results in parallel. However, existing learning-based techniques have a significant drawback: each robot of interest requires a specialized model that must be trained from scratch. To address this shortcoming, we investigate a novel distance-geometric robot representation coupled with a graph structure that allows us to leverage the flexibility of graph neural networks (GNNs). We use this approach to train a generative graphical inverse kinematics solver (GGIK) that is able to produce a large number of diverse solutions in parallel while also generalizing well -- a single learned model can be used to produce IK solutions for a variety of different robots. The graphical formulation elegantly exposes the symmetry and Euclidean equivariance of the IK problem that stems from the spatial nature of robot manipulators. We exploit this symmetry by encoding it into the architecture of our learned model, yielding a flexible solver that is able to produce sets of IK solutions for multiple robots.

CIDGIKc: Distance-Geometric Inverse Kinematics for Continuum Robots

The small size, high dexterity, and intrinsic compliance of continuum robots (CRs) make them well suited for constrained environments. Solving the inverse kinematics (IK), that is finding robot joint configurations that satisfy desired position or pose queries, is a fundamental challenge in motion planning, control, and calibration for any robot structure. For CRs, the need to avoid obstacles in tightly confined workspaces greatly complicates the search for feasible IK solutions. Without an accurate initialization or multiple re-starts, existing algorithms often fail to find a solution. We present CIDGIKc (Convex Iteration for Distance-Geometric Inverse Kinematics for Continuum Robots), an algorithm that solves these nonconvex feasibility problems with a sequence of semidefinite programs whose objectives are designed to encourage low-rank minimizers. CIDGIKc is enabled by a novel distance-geometric parameterization of constant curvature segment geometry for CRs with extensible segments. The resulting IK formulation involves only quadratic expressions and can efficiently incorporate a large number of collision avoidance constraints. Our experimental results demonstrate >98% solve success rates within complex, highly cluttered environments which existing algorithms cannot account for.

The Sum of Its Parts: Visual Part Segmentation for Inertial Parameter Identification of Manipulated Objects

To operate safely and efficiently alongside human workers, collaborative robots (cobots) require the ability to quickly understand the dynamics of manipulated objects. However, traditional methods for estimating the full set of inertial parameters rely on motions that are necessarily fast and unsafe (to achieve a sufficient signal-to-noise ratio). In this work, we take an alternative approach: by combining visual and force-torque measurements, we develop an inertial parameter identification algorithm that requires slow or 'stop-and-go' motions only, and hence is ideally tailored for use around humans. Our technique, called Homogeneous Part Segmentation (HPS), leverages the observation that man-made objects are often composed of distinct, homogeneous parts. We combine a surface-based point clustering method with a volumetric shape segmentation algorithm to quickly produce a part-level segmentation of a manipulated object; the segmented representation is then used by HPS to accurately estimate the object's inertial parameters. To benchmark our algorithm, we create and utilize a novel dataset consisting of realistic meshes, segmented point clouds, and inertial parameters for 20 common workshop tools. Finally, we demonstrate the real-world performance and accuracy of HPS by performing an intricate 'hammer balancing act' autonomously and online with a low-cost collaborative robotic arm. Our code and dataset are open source and freely available.

One Network, Many Robots: Generative Graphical Inverse Kinematics

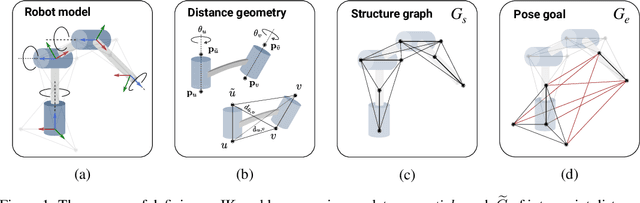
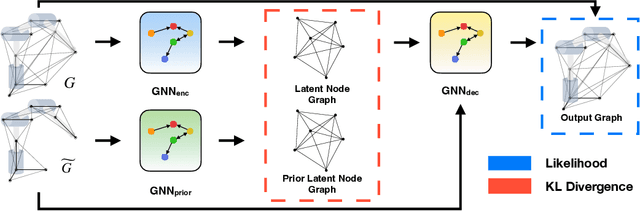
Quickly and reliably finding accurate inverse kinematics (IK) solutions remains a challenging problem for robotic manipulation. Existing numerical solvers are broadly applicable, but rely on local search techniques to manage highly nonconvex objective functions. Recently, learning-based approaches have shown promise as a means to generate fast and accurate IK results; learned solvers can easily be integrated with other learning algorithms in end-to-end systems. However, learning-based methods have an Achilles' heel: each robot of interest requires a specialized model which must be trained from scratch. To address this key shortcoming, we investigate a novel distance-geometric robot representation coupled with a graph structure that allows us to leverage the flexibility of graph neural networks (GNNs). We use this approach to train the first learned generative graphical inverse kinematics (GGIK) solver that is, crucially, "robot-agnostic"-a single model is able to provide IK solutions for a variety of different robots. Additionally, the generative nature of GGIK allows the solver to produce a large number of diverse solutions in parallel with minimal additional computation time, making it appropriate for applications such as sampling-based motion planning. Finally, GGIK can complement local IK solvers by providing reliable initializations. These advantages, as well as the ability to use task-relevant priors and to continuously improve with new data, suggest that GGIK has the potential to be a key component of flexible, learning-based robotic manipulation systems.

Fast Object Inertial Parameter Identification for Collaborative Robots

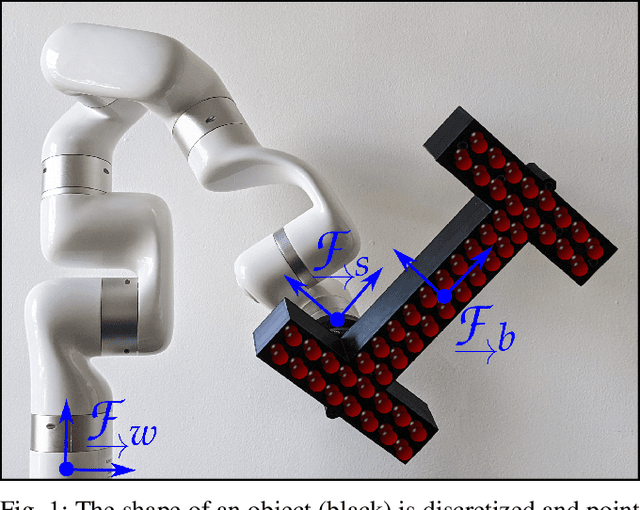
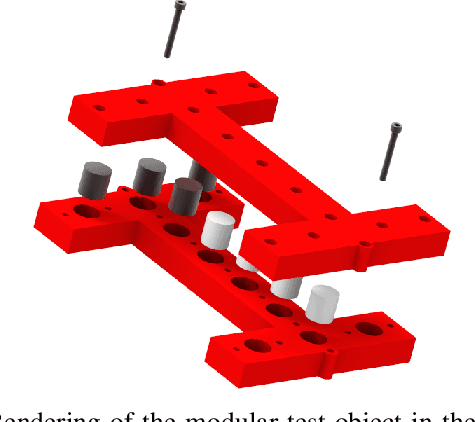
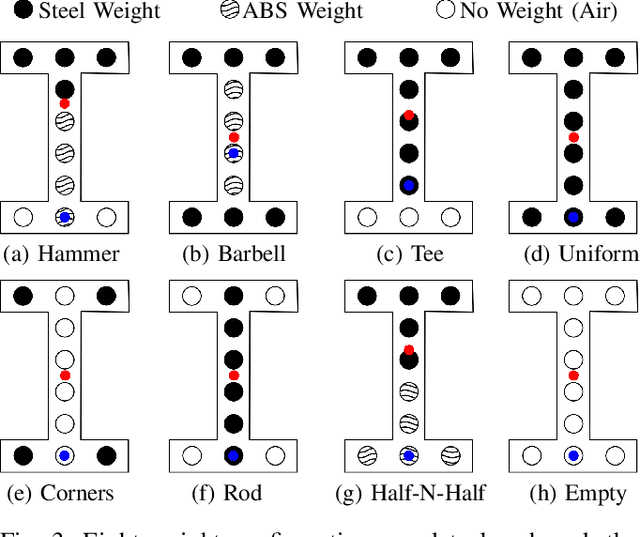
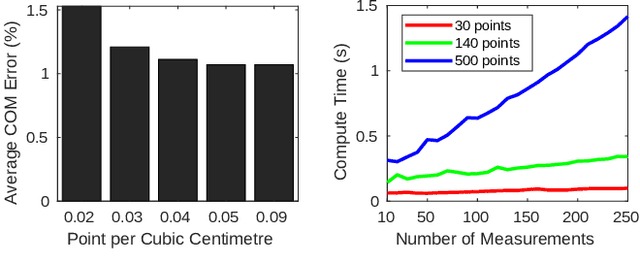
Collaborative robots (cobots) are machines designed to work safely alongside people in human-centric environments. Providing cobots with the ability to quickly infer the inertial parameters of manipulated objects will improve their flexibility and enable greater usage in manufacturing and other areas. To ensure safety, cobots are subject to kinematic limits that result in low signal-to-noise ratios (SNR) for velocity, acceleration, and force-torque data. This renders existing inertial parameter identification algorithms prohibitively slow and inaccurate. Motivated by the desire for faster model acquisition, we investigate the use of an approximation of rigid body dynamics to improve the SNR. Additionally, we introduce a mass discretization method that can make use of shape information to quickly identify plausible inertial parameters for a manipulated object. We present extensive simulation studies and real-world experiments demonstrating that our approach complements existing inertial parameter identification methods by specifically targeting the typical cobot operating regime.

Convex Iteration for Distance-Geometric Inverse Kinematics

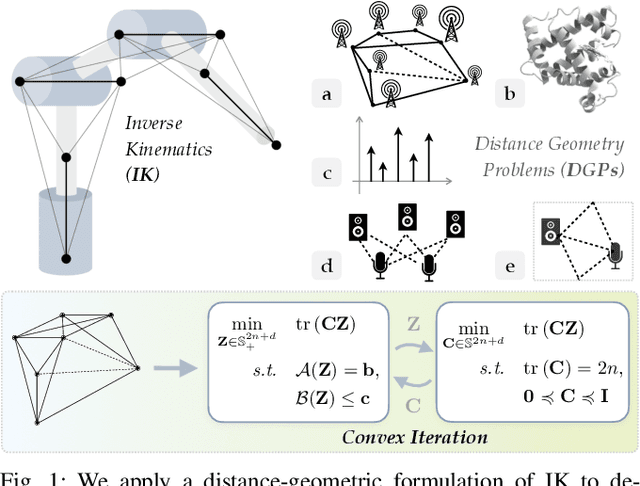
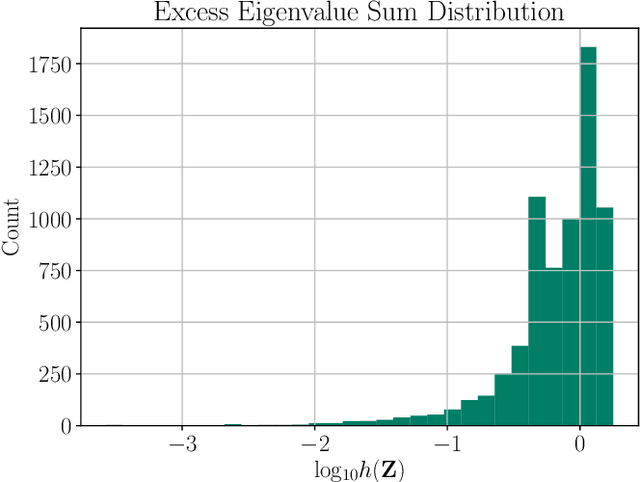
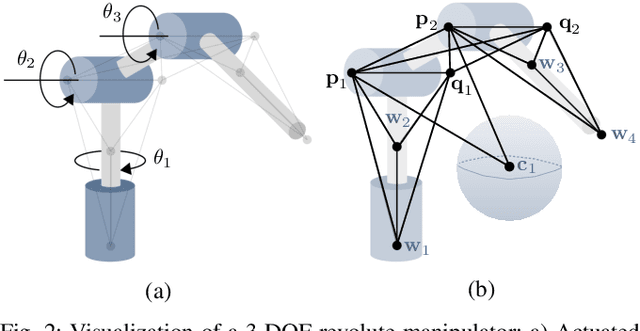
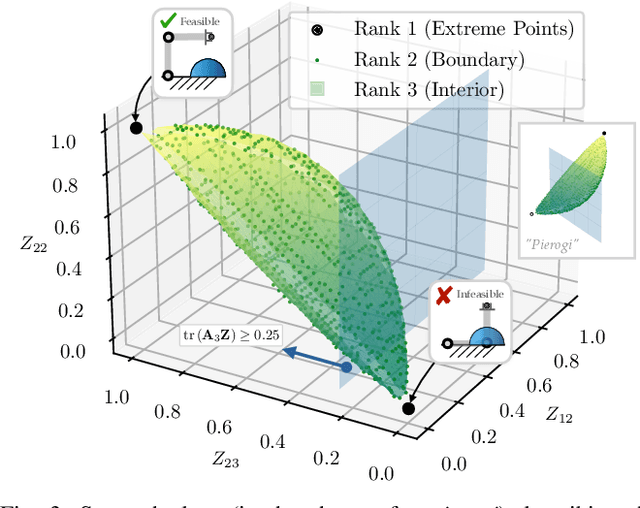
Inverse kinematics (IK) is the problem of finding robot joint configurations that satisfy constraints on the position or pose of one or more end-effectors. For robots with redundant degrees of freedom, there is often an infinite, nonconvex set of solutions. The IK problem is further complicated when collision avoidance constraints are imposed by obstacles in the workspace. In general, closed-form expressions yielding feasible configurations do not exist, motivating the use of numerical solution methods. However, these approaches rely on local optimization of nonconvex problems, often requiring an accurate initialization or numerous re-initializations to converge to a valid solution. In this work, we first formulate complicated inverse kinematics problems as convex feasibility problems whose low-rank feasible points provide exact IK solutions. We then present CIDGIK (Convex Iteration for Distance-Geometric Inverse Kinematics), an algorithm that solves these feasibility problems with a sequence of semidefinite programs whose objectives are designed to encourage low-rank minimizers. Our problem formulation elegantly unifies the configuration space and workspace constraints of a robot: intrinsic robot geometry and obstacle avoidance are both expressed as simple linear matrix equations and inequalities. Our experimental results for a variety of popular manipulator models demonstrate faster and more accurate convergence than a conventional nonlinear optimization-based approach, especially in environments with many obstacles.

Riemannian Optimization for Distance Geometric Inverse Kinematics

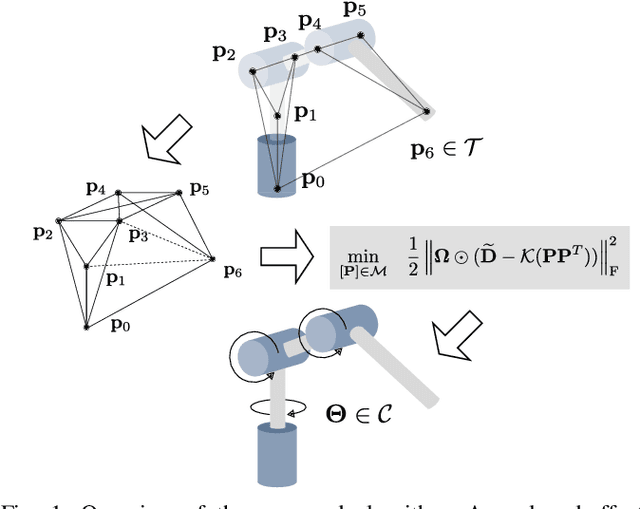
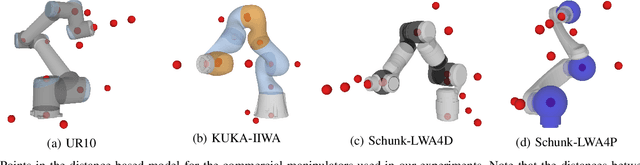
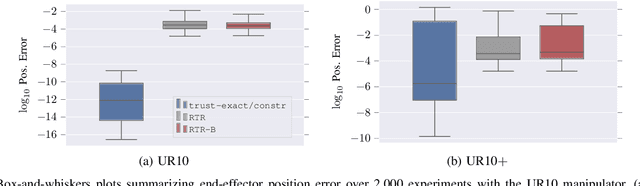
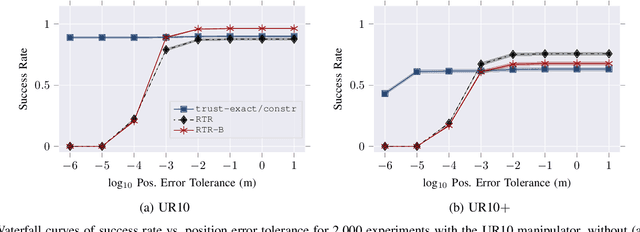
Solving the inverse kinematics problem is a fundamental challenge in motion planning, control, and calibration for articulated robots. Kinematic models for these robots are typically parameterized by joint angles, generating a complicated mapping between a robot's configuration and end-effector pose. Alternatively, the kinematic model and task constraints can be represented using invariant distances between points attached to the robot. In this paper, we formalize the equivalence of distance-based inverse kinematics and the distance geometry problem for a large class of articulated robots and task constraints. Unlike previous approaches, we use the connection between distance geometry and low-rank matrix completion to find inverse kinematics solutions by completing a partial Euclidean distance matrix through local optimization. Furthermore, we parameterize the space of Euclidean distance matrices with the Riemannian manifold of fixed-rank Gram matrices, allowing us to leverage a variety of mature Riemannian optimization methods. Finally, we show that bound smoothing can be used to generate informed initializations without significant computational overhead, improving convergence. We demonstrate that our novel inverse kinematics solver achieves higher success rates than traditional techniques, and significantly outperforms them on problems that involve many workspace constraints.

A Question of Time: Revisiting the Use of Recursive Filtering for Temporal Calibration of Multisensor Systems

We examine the problem of time delay estimation, or temporal calibration, in the context of multisensor data fusion. Differences in processing intervals and other factors typically lead to a relative delay between measurement from two disparate sensors. Correct (optimal) data fusion demands that the relative delay must either be known in advance or identified online. There have been several recent proposals in the literature to determine the delay parameter using recursive, causal filters such as the extended Kalman filter (EKF). We carefully review this formulation and show that there are fundamental issues with the structure of the EKF (and related algorithms) when the delay is included in the filter state vector as a value to be estimated. These structural issues, in turn, leave recursive filters prone to bias and inconsistency. Our theoretical analysis is supported by simulation studies that demonstrate the implications in terms of filter performance; although tuning of the filter noise variances may reduce the chance of inconsistency or divergence, the underlying structural concerns remain. We offer brief suggestions for ways to maintain the computational efficiency of recursive filtering for temporal calibration while avoiding the drawbacks of the standard algorithms.