GISR: Geometric Initialization and Silhouette-based Refinement for Single-View Robot Pose and Configuration Estimation

For autonomous robotics applications, it is crucial that robots are able to accurately measure their potential state and perceive their environment, including other agents within it (e.g., cobots interacting with humans). The redundancy of these measurements is important, as it allows for planning and execution of recovery protocols in the event of sensor failure or external disturbances. Visual estimation can provide this redundancy through the use of low-cost sensors and server as a standalone source of proprioception when no encoder-based sensing is available. Therefore, we estimate the configuration of the robot jointly with its pose, which provides a complete spatial understanding of the observed robot. We present GISR - a method for deep configuration and robot-to-camera pose estimation that prioritizes real-time execution. GISR is comprised of two modules: (i) a geometric initialization module, efficiently computing an approximate robot pose and configuration, and (ii) an iterative silhouette-based refinement module that refines the initial solution in only a few iterations. We evaluate our method on a publicly available dataset and show that GISR performs competitively with existing state-of-the-art approaches, while being significantly faster compared to existing methods of the same class. Our code is available at https://github.com/iwhitey/GISR-robot.

Towards Automated Readable Proofs of Ruler and Compass Constructions

Although there are several systems that successfully generate construction steps for ruler and compass construction problems, none of them provides readable synthetic correctness proofs for generated constructions. In the present work, we demonstrate how our triangle construction solver ArgoTriCS can cooperate with automated theorem provers for first order logic and coherent logic so that it generates construction correctness proofs, that are both human-readable and formal (can be checked by interactive theorem provers such as Coq or Isabelle/HOL). These proofs currently rely on many high-level lemmas and our goal is to have them all formally shown from the basic axioms of geometry.

Euclidean Equivariant Models for Generative Graphical Inverse Kinematics

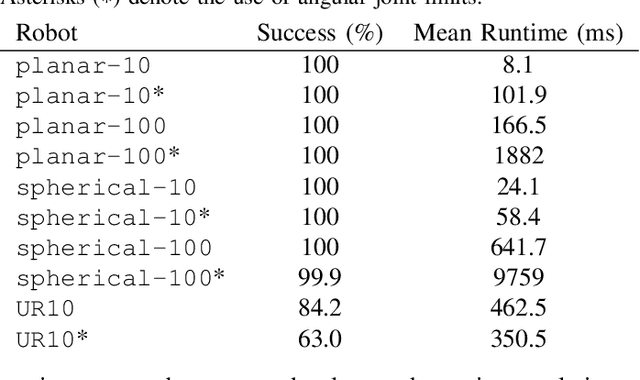
Quickly and reliably finding accurate inverse kinematics (IK) solutions remains a challenging problem for robotic manipulation. Existing numerical solvers typically produce a single solution only and rely on local search techniques to minimize a highly nonconvex objective function. Recently, learning-based approaches that approximate the entire feasible set of solutions have shown promise as a means to generate multiple fast and accurate IK results in parallel. However, existing learning-based techniques have a significant drawback: each robot of interest requires a specialized model that must be trained from scratch. To address this shortcoming, we investigate a novel distance-geometric robot representation coupled with a graph structure that allows us to leverage the flexibility of graph neural networks (GNNs). We use this approach to train a generative graphical inverse kinematics solver (GGIK) that is able to produce a large number of diverse solutions in parallel while also generalizing well -- a single learned model can be used to produce IK solutions for a variety of different robots. The graphical formulation elegantly exposes the symmetry and Euclidean equivariance of the IK problem that stems from the spatial nature of robot manipulators. We exploit this symmetry by encoding it into the architecture of our learned model, yielding a flexible solver that is able to produce sets of IK solutions for multiple robots.

CIDGIKc: Distance-Geometric Inverse Kinematics for Continuum Robots

The small size, high dexterity, and intrinsic compliance of continuum robots (CRs) make them well suited for constrained environments. Solving the inverse kinematics (IK), that is finding robot joint configurations that satisfy desired position or pose queries, is a fundamental challenge in motion planning, control, and calibration for any robot structure. For CRs, the need to avoid obstacles in tightly confined workspaces greatly complicates the search for feasible IK solutions. Without an accurate initialization or multiple re-starts, existing algorithms often fail to find a solution. We present CIDGIKc (Convex Iteration for Distance-Geometric Inverse Kinematics for Continuum Robots), an algorithm that solves these nonconvex feasibility problems with a sequence of semidefinite programs whose objectives are designed to encourage low-rank minimizers. CIDGIKc is enabled by a novel distance-geometric parameterization of constant curvature segment geometry for CRs with extensible segments. The resulting IK formulation involves only quadratic expressions and can efficiently incorporate a large number of collision avoidance constraints. Our experimental results demonstrate >98% solve success rates within complex, highly cluttered environments which existing algorithms cannot account for.

A Distance-Geometric Method for Recovering Robot Joint Angles From an RGB Image

Autonomous manipulation systems operating in domains where human intervention is difficult or impossible (e.g., underwater, extraterrestrial or hazardous environments) require a high degree of robustness to sensing and communication failures. Crucially, motion planning and control algorithms require a stream of accurate joint angle data provided by joint encoders, the failure of which may result in an unrecoverable loss of functionality. In this paper, we present a novel method for retrieving the joint angles of a robot manipulator using only a single RGB image of its current configuration, opening up an avenue for recovering system functionality when conventional proprioceptive sensing is unavailable. Our approach, based on a distance-geometric representation of the configuration space, exploits the knowledge of a robot's kinematic model with the goal of training a shallow neural network that performs a 2D-to-3D regression of distances associated with detected structural keypoints. It is shown that the resulting Euclidean distance matrix uniquely corresponds to the observed configuration, where joint angles can be recovered via multidimensional scaling and a simple inverse kinematics procedure. We evaluate the performance of our approach on real RGB images of a Franka Emika Panda manipulator, showing that the proposed method is efficient and exhibits solid generalization ability. Furthermore, we show that our method can be easily combined with a dense refinement technique to obtain superior results.

One Network, Many Robots: Generative Graphical Inverse Kinematics

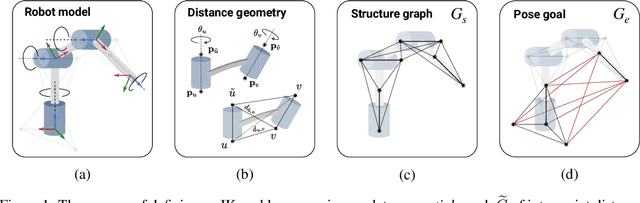
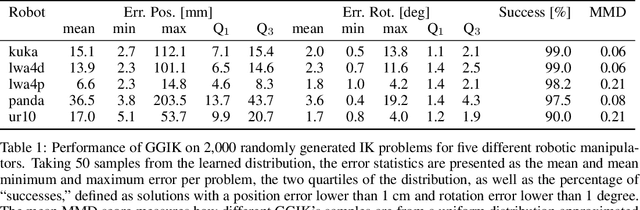
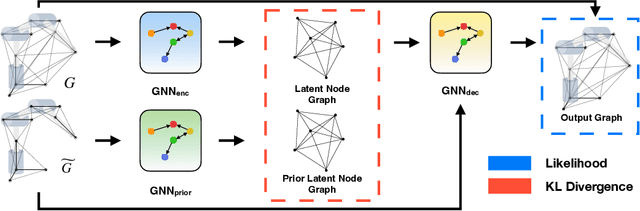
Quickly and reliably finding accurate inverse kinematics (IK) solutions remains a challenging problem for robotic manipulation. Existing numerical solvers are broadly applicable, but rely on local search techniques to manage highly nonconvex objective functions. Recently, learning-based approaches have shown promise as a means to generate fast and accurate IK results; learned solvers can easily be integrated with other learning algorithms in end-to-end systems. However, learning-based methods have an Achilles' heel: each robot of interest requires a specialized model which must be trained from scratch. To address this key shortcoming, we investigate a novel distance-geometric robot representation coupled with a graph structure that allows us to leverage the flexibility of graph neural networks (GNNs). We use this approach to train the first learned generative graphical inverse kinematics (GGIK) solver that is, crucially, "robot-agnostic"-a single model is able to provide IK solutions for a variety of different robots. Additionally, the generative nature of GGIK allows the solver to produce a large number of diverse solutions in parallel with minimal additional computation time, making it appropriate for applications such as sampling-based motion planning. Finally, GGIK can complement local IK solvers by providing reliable initializations. These advantages, as well as the ability to use task-relevant priors and to continuously improve with new data, suggest that GGIK has the potential to be a key component of flexible, learning-based robotic manipulation systems.

Convex Iteration for Distance-Geometric Inverse Kinematics

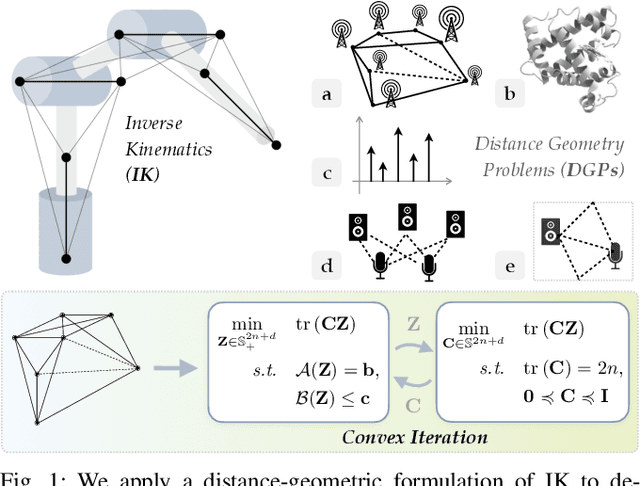
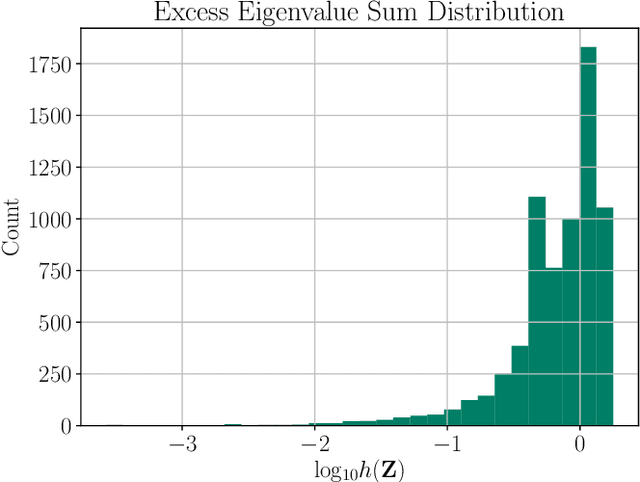
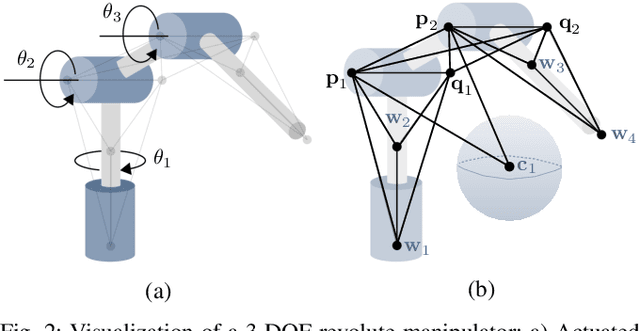
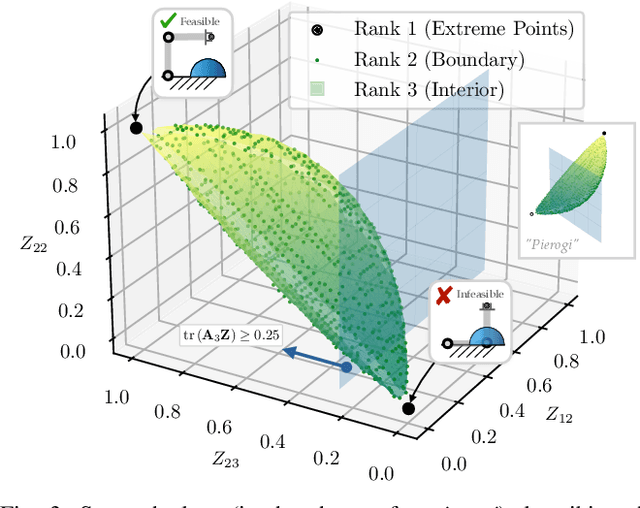
Inverse kinematics (IK) is the problem of finding robot joint configurations that satisfy constraints on the position or pose of one or more end-effectors. For robots with redundant degrees of freedom, there is often an infinite, nonconvex set of solutions. The IK problem is further complicated when collision avoidance constraints are imposed by obstacles in the workspace. In general, closed-form expressions yielding feasible configurations do not exist, motivating the use of numerical solution methods. However, these approaches rely on local optimization of nonconvex problems, often requiring an accurate initialization or numerous re-initializations to converge to a valid solution. In this work, we first formulate complicated inverse kinematics problems as convex feasibility problems whose low-rank feasible points provide exact IK solutions. We then present CIDGIK (Convex Iteration for Distance-Geometric Inverse Kinematics), an algorithm that solves these feasibility problems with a sequence of semidefinite programs whose objectives are designed to encourage low-rank minimizers. Our problem formulation elegantly unifies the configuration space and workspace constraints of a robot: intrinsic robot geometry and obstacle avoidance are both expressed as simple linear matrix equations and inequalities. Our experimental results for a variety of popular manipulator models demonstrate faster and more accurate convergence than a conventional nonlinear optimization-based approach, especially in environments with many obstacles.

Riemannian Optimization for Distance Geometric Inverse Kinematics

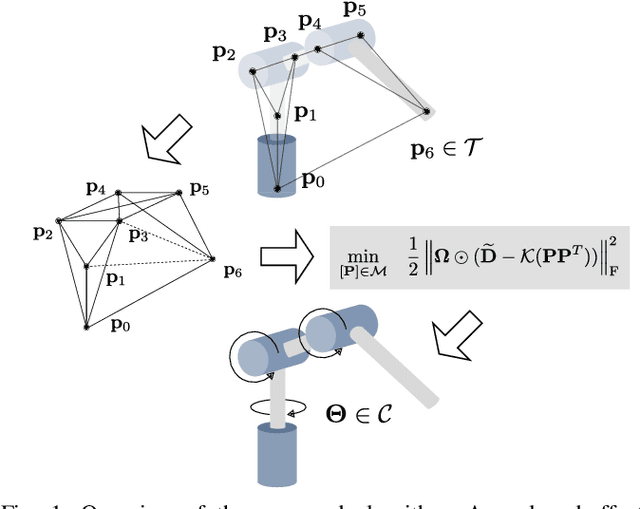
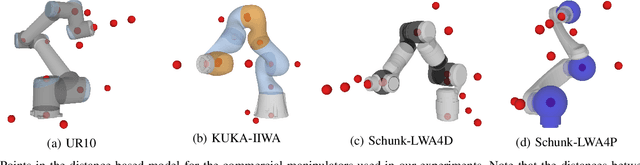
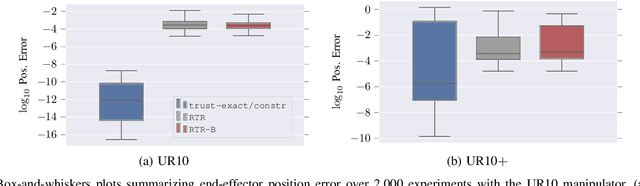
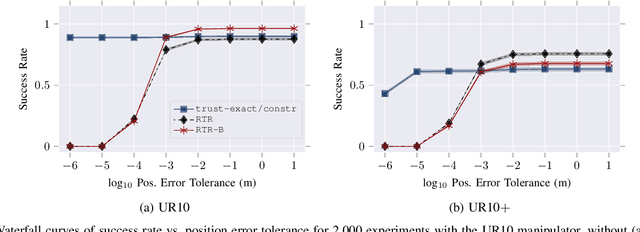
Solving the inverse kinematics problem is a fundamental challenge in motion planning, control, and calibration for articulated robots. Kinematic models for these robots are typically parameterized by joint angles, generating a complicated mapping between a robot's configuration and end-effector pose. Alternatively, the kinematic model and task constraints can be represented using invariant distances between points attached to the robot. In this paper, we formalize the equivalence of distance-based inverse kinematics and the distance geometry problem for a large class of articulated robots and task constraints. Unlike previous approaches, we use the connection between distance geometry and low-rank matrix completion to find inverse kinematics solutions by completing a partial Euclidean distance matrix through local optimization. Furthermore, we parameterize the space of Euclidean distance matrices with the Riemannian manifold of fixed-rank Gram matrices, allowing us to leverage a variety of mature Riemannian optimization methods. Finally, we show that bound smoothing can be used to generate informed initializations without significant computational overhead, improving convergence. We demonstrate that our novel inverse kinematics solver achieves higher success rates than traditional techniques, and significantly outperforms them on problems that involve many workspace constraints.

A Riemannian Metric for Geometry-Aware Singularity Avoidance by Articulated Robots

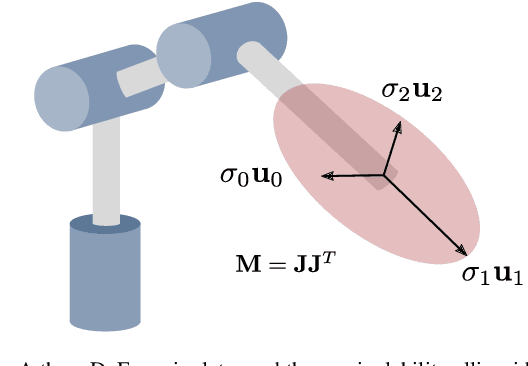
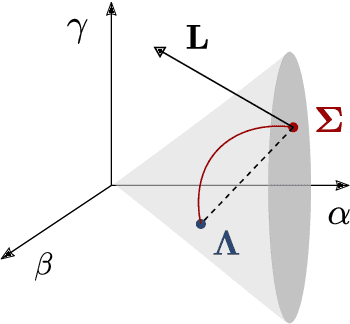
Articulated robots such as manipulators increasingly must operate in uncertain and dynamic environments where interaction (with human coworkers, for example) is necessary. In these situations, the capacity to quickly adapt to unexpected changes in operational space constraints is essential. At certain points in a manipulator's configuration space, termed singularities, the robot loses one or more degrees of freedom (DoF) and is unable to move in specific operational space directions. The inability to move in arbitrary directions in operational space compromises adaptivity and, potentially, safety. We introduce a geometry-aware singularity index,defined using a Riemannian metric on the manifold of symmetric positive definite matrices, to provide a measure of proximity to singular configurations. We demonstrate that our index avoids some of the failure modes and difficulties inherent to other common indices. Further, we show that this index can be differentiated easily, making it compatible with local optimization approaches used for operational space control. Our experimental results establish that, for reaching and path following tasks, optimization based on our index outperforms a common manipulability maximization technique, ensuring singularity-robust motions.

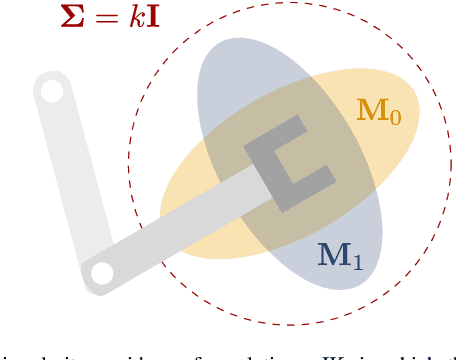
Inverse Kinematics as Low-Rank Euclidean Distance Matrix Completion

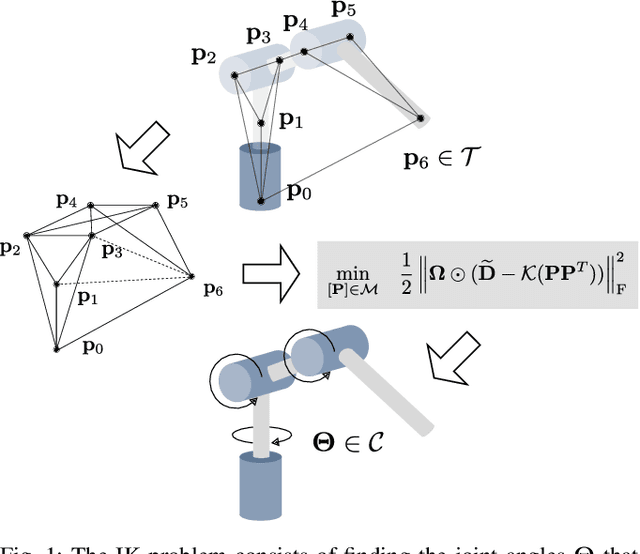
The majority of inverse kinematics (IK) algorithms search for solutions in a configuration space defined by joint angles. However, the kinematics of many robots can also be described in terms of distances between rigidly-attached points, which collectively form a Euclidean distance matrix. This alternative geometric description of the kinematics reveals an elegant equivalence between IK and the problem of low-rank matrix completion. We use this connection to implement a novel Riemannian optimization-based solution to IK for various articulated robots with symmetric joint angle constraints.