Semi-Implicit Variational Inference via Kernelized Path Gradient Descent

Semi-implicit variational inference (SIVI) is a powerful framework for approximating complex posterior distributions, but training with the Kullback-Leibler (KL) divergence can be challenging due to high variance and bias in high-dimensional settings. While current state-of-the-art semi-implicit variational inference methods, particularly Kernel Semi-Implicit Variational Inference (KSIVI), have been shown to work in high dimensions, training remains moderately expensive. In this work, we propose a kernelized KL divergence estimator that stabilizes training through nonparametric smoothing. To further reduce the bias, we introduce an importance sampling correction. We provide a theoretical connection to the amortized version of the Stein variational gradient descent, which estimates the score gradient via Stein's identity, showing that both methods minimize the same objective, but our semi-implicit approach achieves lower gradient variance. In addition, our method's bias in function space is benign, leading to more stable and efficient optimization. Empirical results demonstrate that our method outperforms or matches state-of-the-art SIVI methods in both performance and training efficiency.

Revisiting Unbiased Implicit Variational Inference

Recent years have witnessed growing interest in semi-implicit variational inference (SIVI) methods due to their ability to rapidly generate samples from complex distributions. However, since the likelihood of these samples is non-trivial to estimate in high dimensions, current research focuses on finding effective SIVI training routines. Although unbiased implicit variational inference (UIVI) has largely been dismissed as imprecise and computationally prohibitive because of its inner MCMC loop, we revisit this method and show that UIVI's MCMC loop can be effectively replaced via importance sampling and the optimal proposal distribution can be learned stably by minimizing an expected forward Kullback-Leibler divergence without bias. Our refined approach demonstrates superior performance or parity with state-of-the-art methods on established SIVI benchmarks.

How Inverse Conditional Flows Can Serve as a Substitute for Distributional Regression

Neural network representations of simple models, such as linear regression, are being studied increasingly to better understand the underlying principles of deep learning algorithms. However, neural representations of distributional regression models, such as the Cox model, have received little attention so far. We close this gap by proposing a framework for distributional regression using inverse flow transformations (DRIFT), which includes neural representations of the aforementioned models. We empirically demonstrate that the neural representations of models in DRIFT can serve as a substitute for their classical statistical counterparts in several applications involving continuous, ordered, time-series, and survival outcomes. We confirm that models in DRIFT empirically match the performance of several statistical methods in terms of estimation of partial effects, prediction, and aleatoric uncertainty quantification. DRIFT covers both interpretable statistical models and flexible neural networks opening up new avenues in both statistical modeling and deep learning.

Multi-Objective Hyperparameter Optimization -- An Overview

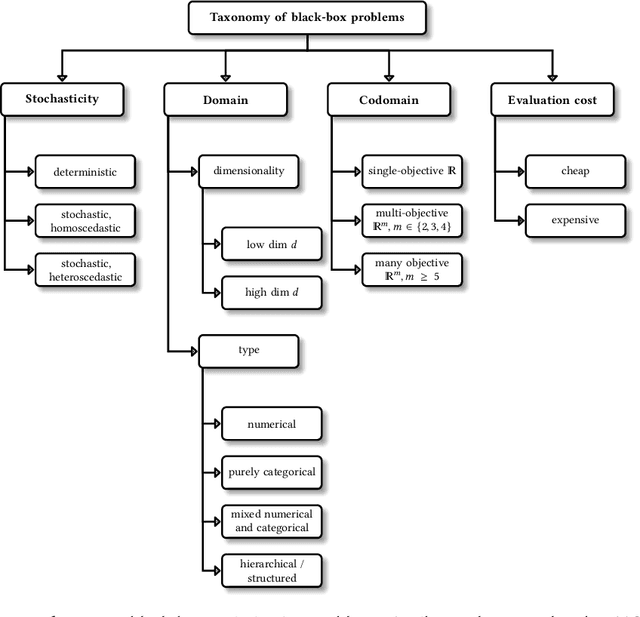
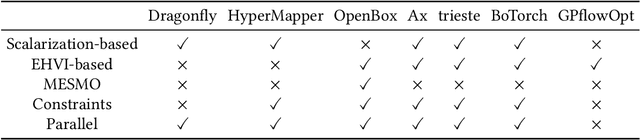
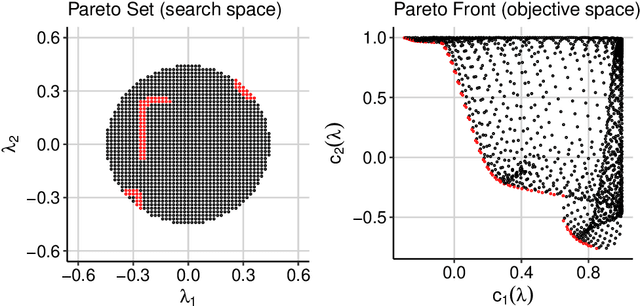
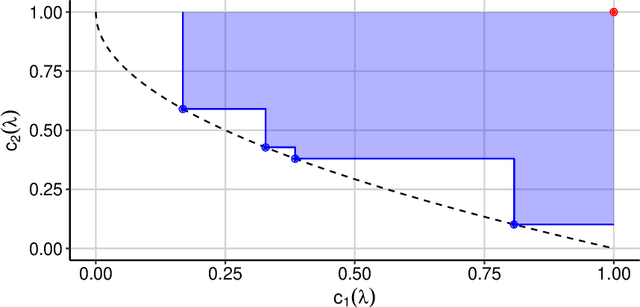
Hyperparameter optimization constitutes a large part of typical modern machine learning workflows. This arises from the fact that machine learning methods and corresponding preprocessing steps often only yield optimal performance when hyperparameters are properly tuned. But in many applications, we are not only interested in optimizing ML pipelines solely for predictive accuracy; additional metrics or constraints must be considered when determining an optimal configuration, resulting in a multi-objective optimization problem. This is often neglected in practice, due to a lack of knowledge and readily available software implementations for multi-objective hyperparameter optimization. In this work, we introduce the reader to the basics of multi- objective hyperparameter optimization and motivate its usefulness in applied ML. Furthermore, we provide an extensive survey of existing optimization strategies, both from the domain of evolutionary algorithms and Bayesian optimization. We illustrate the utility of MOO in several specific ML applications, considering objectives such as operating conditions, prediction time, sparseness, fairness, interpretability and robustness.

Hyperparameter Optimization: Foundations, Algorithms, Best Practices and Open Challenges

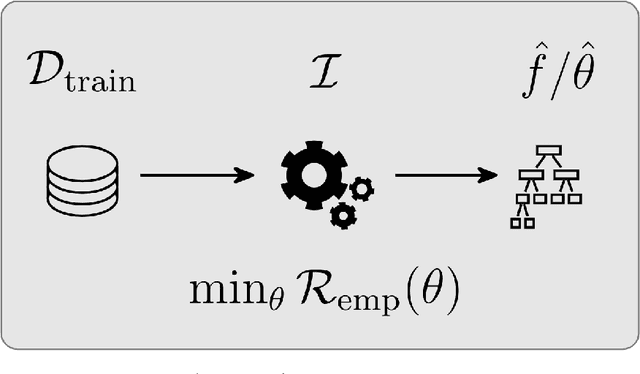
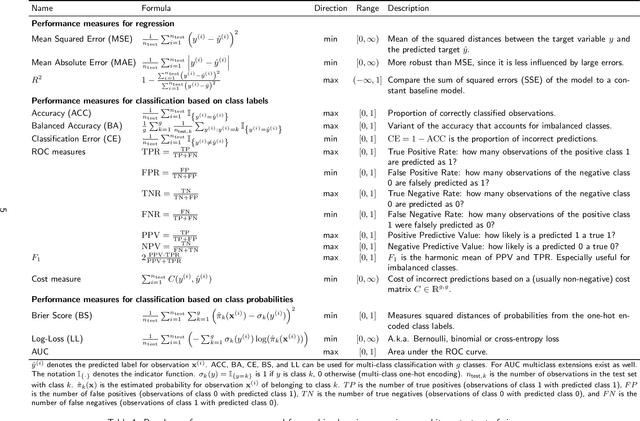
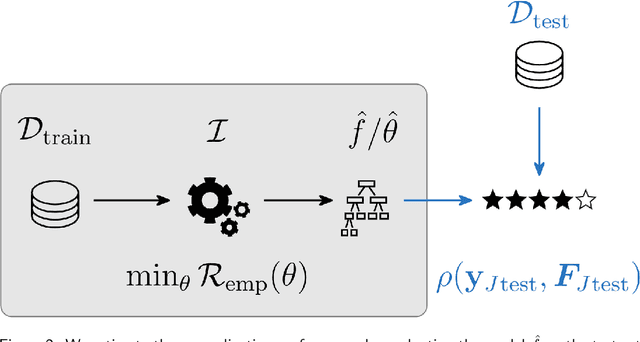
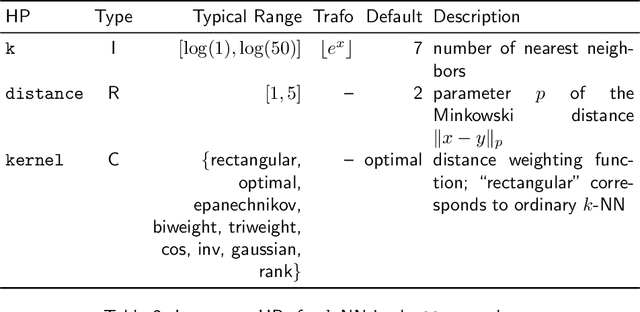
Most machine learning algorithms are configured by one or several hyperparameters that must be carefully chosen and often considerably impact performance. To avoid a time consuming and unreproducible manual trial-and-error process to find well-performing hyperparameter configurations, various automatic hyperparameter optimization (HPO) methods, e.g., based on resampling error estimation for supervised machine learning, can be employed. After introducing HPO from a general perspective, this paper reviews important HPO methods such as grid or random search, evolutionary algorithms, Bayesian optimization, Hyperband and racing. It gives practical recommendations regarding important choices to be made when conducting HPO, including the HPO algorithms themselves, performance evaluation, how to combine HPO with ML pipelines, runtime improvements, and parallelization.