Hybrid Bernstein Normalizing Flows for Flexible Multivariate Density Regression with Interpretable Marginals

Density regression models allow a comprehensive understanding of data by modeling the complete conditional probability distribution. While flexible estimation approaches such as normalizing flows (NF) work particularly well in multiple dimensions, interpreting the input-output relationship of such models is often difficult, due to the black-box character of deep learning models. In contrast, existing statistical methods for multivariate outcomes such as multivariate conditional transformation models (MCTM) are restricted in flexibility and are often not expressive enough to represent complex multivariate probability distributions. In this paper, we combine MCTM with state-of-the-art and autoregressive NF to leverage the transparency of MCTM for modeling interpretable feature effects on the marginal distributions in the first step and the flexibility of neural-network-based NF techniques to account for complex and non-linear relationships in the joint data distribution. We demonstrate our method's versatility in various numerical experiments and compare it with MCTM and other NF models on both simulated and real-world data.

How Inverse Conditional Flows Can Serve as a Substitute for Distributional Regression

Neural network representations of simple models, such as linear regression, are being studied increasingly to better understand the underlying principles of deep learning algorithms. However, neural representations of distributional regression models, such as the Cox model, have received little attention so far. We close this gap by proposing a framework for distributional regression using inverse flow transformations (DRIFT), which includes neural representations of the aforementioned models. We empirically demonstrate that the neural representations of models in DRIFT can serve as a substitute for their classical statistical counterparts in several applications involving continuous, ordered, time-series, and survival outcomes. We confirm that models in DRIFT empirically match the performance of several statistical methods in terms of estimation of partial effects, prediction, and aleatoric uncertainty quantification. DRIFT covers both interpretable statistical models and flexible neural networks opening up new avenues in both statistical modeling and deep learning.

Short-Term Density Forecasting of Low-Voltage Load using Bernstein-Polynomial Normalizing Flows

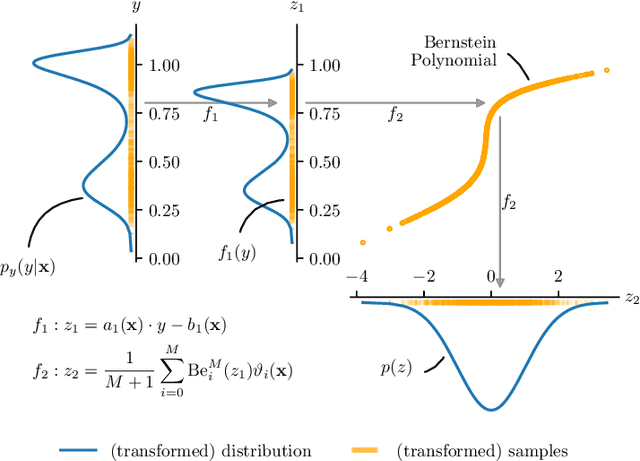
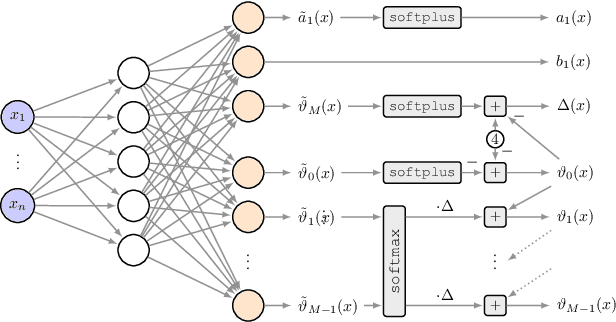
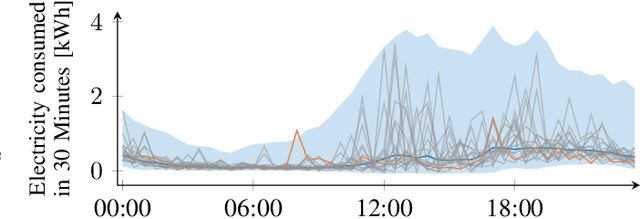
The transition to a fully renewable energy grid requires better forecasting of demand at the low-voltage level to increase efficiency and ensure reliable control. However, high fluctuations and increasing electrification cause huge forecast variability, not reflected in traditional point estimates. Probabilistic load forecasts take future uncertainties into account and thus allow more informed decision-making for the planning and operation of low-carbon energy systems. We propose an approach for flexible conditional density forecasting of short-term load based on Bernstein polynomial normalizing flows, where a neural network controls the parameters of the flow. In an empirical study with 363 smart meter customers, our density predictions compare favorably against Gaussian and Gaussian mixture densities. Also, they outperform a non-parametric approach based on the pinball loss for 24h-ahead load forecasting for two different neural network architectures.