Learning the Uncertainty Sets for Control Dynamics via Set Membership: A Non-Asymptotic Analysis

Set-membership estimation is commonly used in adaptive/learning-based control algorithms that require robustness over the model uncertainty sets, e.g., online robustly stabilizing control and robust adaptive model predictive control. Despite having broad applications, non-asymptotic estimation error bounds in the stochastic setting are limited. This paper provides such a non-asymptotic bound on the diameter of the uncertainty sets generated by set membership estimation on linear dynamical systems under bounded, i.i.d. disturbances. Further, this result is applied to robust adaptive model predictive control with uncertainty sets updated by set membership. We numerically demonstrate the performance of the robust adaptive controller, which rapidly approaches the performance of the offline optimal model predictive controller, in comparison with the control design based on least square estimation's confidence regions.

Coupled Gradient Flows for Strategic Non-Local Distribution Shift

We propose a novel framework for analyzing the dynamics of distribution shift in real-world systems that captures the feedback loop between learning algorithms and the distributions on which they are deployed. Prior work largely models feedback-induced distribution shift as adversarial or via an overly simplistic distribution-shift structure. In contrast, we propose a coupled partial differential equation model that captures fine-grained changes in the distribution over time by accounting for complex dynamics that arise due to strategic responses to algorithmic decision-making, non-local endogenous population interactions, and other exogenous sources of distribution shift. We consider two common settings in machine learning: cooperative settings with information asymmetries, and competitive settings where a learner faces strategic users. For both of these settings, when the algorithm retrains via gradient descent, we prove asymptotic convergence of the retraining procedure to a steady-state, both in finite and in infinite dimensions, obtaining explicit rates in terms of the model parameters. To do so we derive new results on the convergence of coupled PDEs that extends what is known on multi-species systems. Empirically, we show that our approach captures well-documented forms of distribution shifts like polarization and disparate impacts that simpler models cannot capture.

Signal Enhancement for Magnetic Navigation Challenge Problem

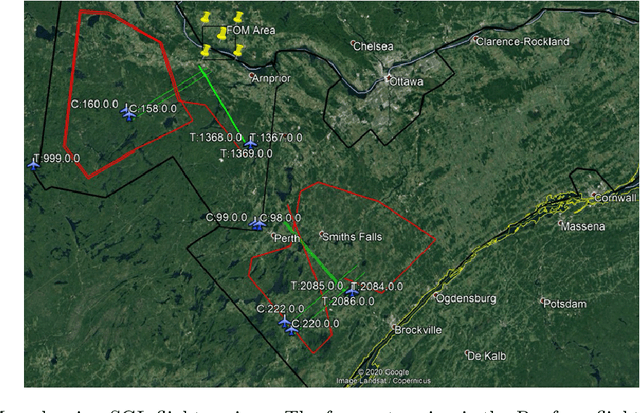
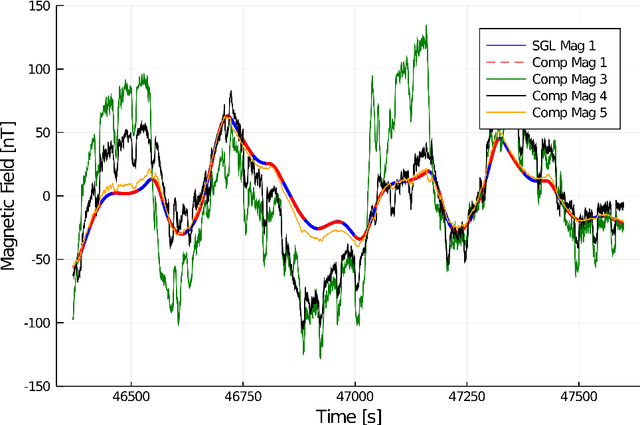
Harnessing the magnetic field of the earth for navigation has shown promise as a viable alternative to other navigation systems. A magnetic navigation system collects its own magnetic field data using a magnetometer and uses magnetic anomaly maps to determine the current location. The greatest challenge with magnetic navigation arises when the magnetic field data from the magnetometer on the navigation system encompass the magnetic field from not just the earth, but also from the vehicle on which it is mounted. It is difficult to separate the earth magnetic anomaly field magnitude, which is crucial for navigation, from the total magnetic field magnitude reading from the sensor. The purpose of this challenge problem is to decouple the earth and aircraft magnetic signals in order to derive a clean signal from which to perform magnetic navigation. Baseline testing on the dataset shows that the earth magnetic field can be extracted from the total magnetic field using machine learning (ML). The challenge is to remove the aircraft magnetic field from the total magnetic field using a trained neural network. These challenges offer an opportunity to construct an effective neural network for removing the aircraft magnetic field from the dataset, using an ML algorithm integrated with physics of magnetic navigation.