Optimal Exploration is no harder than Thompson Sampling

Given a set of arms $\mathcal{Z}\subset \mathbb{R}^d$ and an unknown parameter vector $\theta_\ast\in\mathbb{R}^d$, the pure exploration linear bandit problem aims to return $\arg\max_{z\in \mathcal{Z}} z^{\top}\theta_{\ast}$, with high probability through noisy measurements of $x^{\top}\theta_{\ast}$ with $x\in \mathcal{X}\subset \mathbb{R}^d$. Existing (asymptotically) optimal methods require either a) potentially costly projections for each arm $z\in \mathcal{Z}$ or b) explicitly maintaining a subset of $\mathcal{Z}$ under consideration at each time. This complexity is at odds with the popular and simple Thompson Sampling algorithm for regret minimization, which just requires access to a posterior sampling and argmax oracle, and does not need to enumerate $\mathcal{Z}$ at any point. Unfortunately, Thompson sampling is known to be sub-optimal for pure exploration. In this work, we pose a natural question: is there an algorithm that can explore optimally and only needs the same computational primitives as Thompson Sampling? We answer the question in the affirmative. We provide an algorithm that leverages only sampling and argmax oracles and achieves an exponential convergence rate, with the exponent being the optimal among all possible allocations asymptotically. In addition, we show that our algorithm can be easily implemented and performs as well empirically as existing asymptotically optimal methods.

Instance-optimal PAC Algorithms for Contextual Bandits

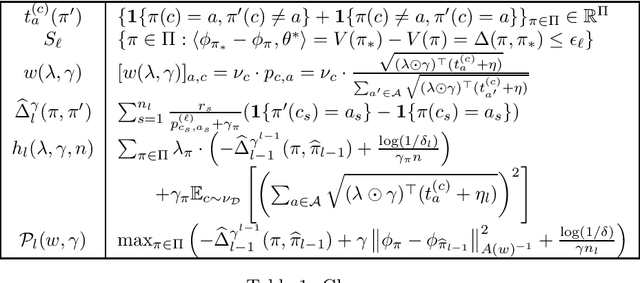
In the stochastic contextual bandit setting, regret-minimizing algorithms have been extensively researched, but their instance-minimizing best-arm identification counterparts remain seldom studied. In this work, we focus on the stochastic bandit problem in the $(\epsilon,\delta)$-$\textit{PAC}$ setting: given a policy class $\Pi$ the goal of the learner is to return a policy $\pi\in \Pi$ whose expected reward is within $\epsilon$ of the optimal policy with probability greater than $1-\delta$. We characterize the first $\textit{instance-dependent}$ PAC sample complexity of contextual bandits through a quantity $\rho_{\Pi}$, and provide matching upper and lower bounds in terms of $\rho_{\Pi}$ for the agnostic and linear contextual best-arm identification settings. We show that no algorithm can be simultaneously minimax-optimal for regret minimization and instance-dependent PAC for best-arm identification. Our main result is a new instance-optimal and computationally efficient algorithm that relies on a polynomial number of calls to an argmax oracle.

Exploration of Numerical Precision in Deep Neural Networks

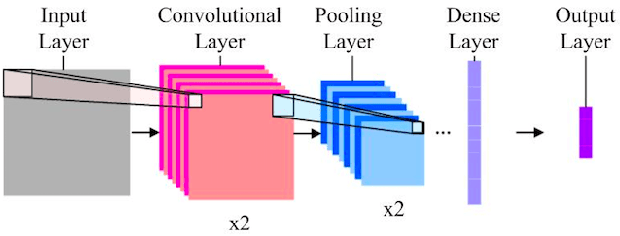
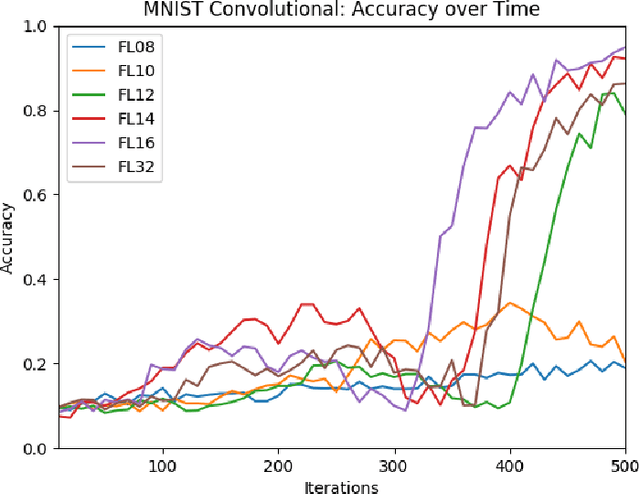
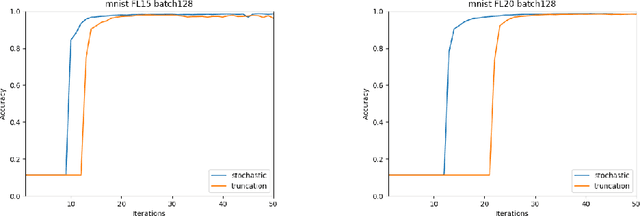
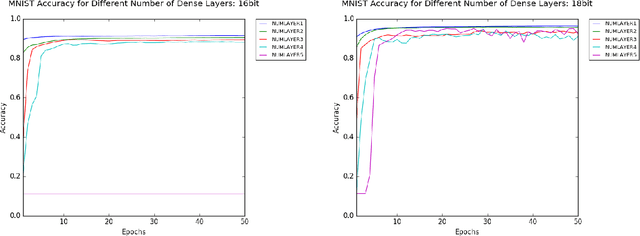
Reduced numerical precision is a common technique to reduce computational cost in many Deep Neural Networks (DNNs). While it has been observed that DNNs are resilient to small errors and noise, no general result exists that is capable of predicting a given DNN system architecture's sensitivity to reduced precision. In this project, we emulate arbitrary bit-width using a specified floating-point representation with a truncation method, which is applied to the neural network after each batch. We explore the impact of several model parameters on the network's training accuracy and show results on the MNIST dataset. We then present a preliminary theoretical investigation of the error scaling in both forward and backward propagations. We end with a discussion of the implications of these results as well as the potential for generalization to other network architectures.