Léon Bottou
FAIR
Memory Mosaics
May 10, 2024



Abstract:Memory Mosaics are networks of associative memories working in concert to achieve a prediction task of interest. Like transformers, memory mosaics possess compositional capabilities and in-context learning capabilities. Unlike transformers, memory mosaics achieve these capabilities in comparatively transparent ways. We demonstrate these capabilities on toy examples and we also show that memory mosaics perform as well or better than transformers on medium-scale language modeling tasks.
Fine-tuning with Very Large Dropout
Mar 01, 2024



Abstract:It is impossible today to pretend that the practice of machine learning is compatible with the idea that training and testing data follow the same distribution. Several authors have recently used ensemble techniques to show how scenarios involving multiple data distributions are best served by representations that are both richer than those obtained by regularizing for the best in-distribution performance, and richer than those obtained under the influence of the implicit sparsity bias of common stochastic gradient procedures. This contribution investigates the use of very high dropout rates instead of ensembles to obtain such rich representations. Although training a deep network from scratch using such dropout rates is virtually impossible, fine-tuning a large pre-trained model under such conditions is not only possible but also achieves out-of-distribution performances that exceed those of both ensembles and weight averaging methods such as model soups. This result has practical significance because the importance of the fine-tuning scenario has considerably grown in recent years. This result also provides interesting insights on the nature of rich representations and on the intrinsically linear nature of fine-tuning a large network using a comparatively small dataset.
Borges and AI
Oct 04, 2023Abstract:Many believe that Large Language Models (LLMs) open the era of Artificial Intelligence (AI). Some see opportunities while others see dangers. Yet both proponents and opponents grasp AI through the imagery popularised by science fiction. Will the machine become sentient and rebel against its creators? Will we experience a paperclip apocalypse? Before answering such questions, we should first ask whether this mental imagery provides a good description of the phenomenon at hand. Understanding weather patterns through the moods of the gods only goes so far. The present paper instead advocates understanding LLMs and their connection to AI through the imagery of Jorge Luis Borges, a master of 20th century literature, forerunner of magical realism, and precursor to postmodern literature. This exercise leads to a new perspective that illuminates the relation between language modelling and artificial intelligence.
Recycling diverse models for out-of-distribution generalization
Dec 20, 2022



Abstract:Foundation models are redefining how AI systems are built. Practitioners now follow a standard procedure to build their machine learning solutions: download a copy of a foundation model, and fine-tune it using some in-house data about the target task of interest. Consequently, the Internet is swarmed by a handful of foundation models fine-tuned on many diverse tasks. Yet, these individual fine-tunings often lack strong generalization and exist in isolation without benefiting from each other. In our opinion, this is a missed opportunity, as these specialized models contain diverse features. Based on this insight, we propose model recycling, a simple strategy that leverages multiple fine-tunings of the same foundation model on diverse auxiliary tasks, and repurposes them as rich and diverse initializations for the target task. Specifically, model recycling fine-tunes in parallel each specialized model on the target task, and then averages the weights of all target fine-tunings into a final model. Empirically, we show that model recycling maximizes model diversity by benefiting from diverse auxiliary tasks, and achieves a new state of the art on the reference DomainBed benchmark for out-of-distribution generalization. Looking forward, model recycling is a contribution to the emerging paradigm of updatable machine learning where, akin to open-source software development, the community collaborates to incrementally and reliably update machine learning models.
Learning useful representations for shifting tasks and distributions
Dec 14, 2022



Abstract:Does the dominant approach to learn representations (as a side effect of optimizing an expected cost for a single training distribution) remain a good approach when we are dealing with multiple distributions. Our thesis is that such scenarios are better served by representations that are "richer" than those obtained with a single optimization episode. This is supported by a collection of empirical results obtained with an apparently na\"ive ensembling technique: concatenating the representations obtained with multiple training episodes using the same data, model, algorithm, and hyper-parameters, but different random seeds. These independently trained networks perform similarly. Yet, in a number of scenarios involving new distributions, the concatenated representation performs substantially better than an equivalently sized network trained from scratch. This proves that the representations constructed by multiple training episodes are in fact different. Although their concatenation carries little additional information about the training task under the training distribution, it becomes substantially more informative when tasks or distributions change. Meanwhile, a single training episode is unlikely to yield such a redundant representation because the optimization process has no reason to accumulate features that do not incrementally improve the training performance.
Rich Feature Construction for the Optimization-Generalization Dilemma
Mar 24, 2022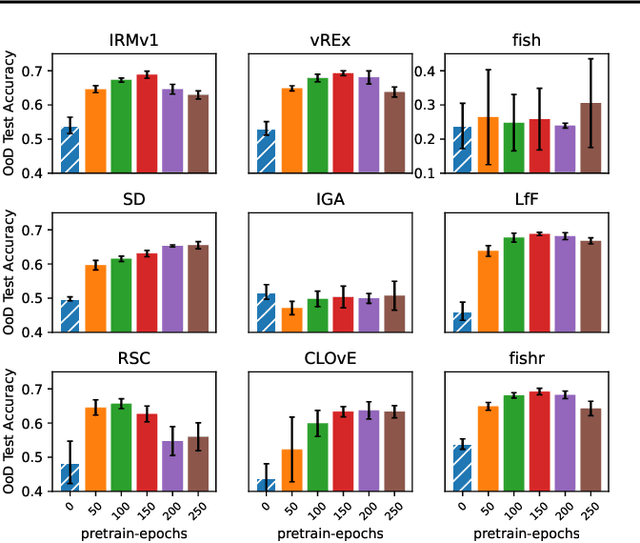
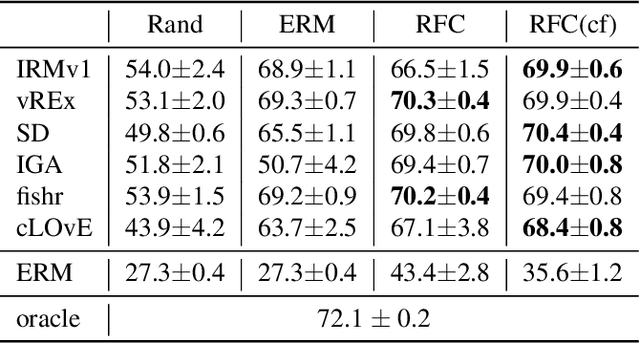
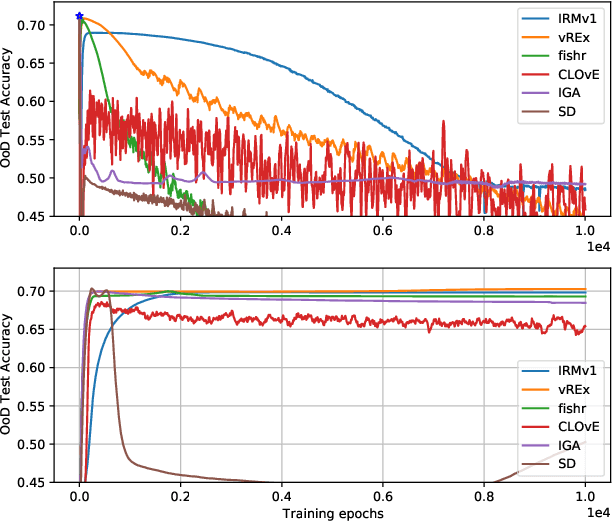
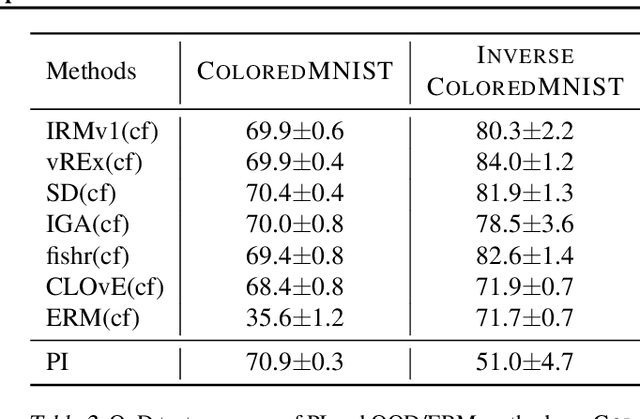
Abstract:There often is a dilemma between ease of optimization and robust out-of-distribution (OoD) generalization. For instance, many OoD methods rely on penalty terms whose optimization is challenging. They are either too strong to optimize reliably or too weak to achieve their goals. In order to escape this dilemma, we propose to first construct a rich representation (RFC) containing a palette of potentially useful features, ready to be used by even simple models. On the one hand, a rich representation provides a good initialization for the optimizer. On the other hand, it also provides an inductive bias that helps OoD generalization. RFC is constructed in a succession of training episodes. During each step of the discovery phase, we craft a multi-objective optimization criterion and its associated datasets in a manner that prevents the network from using the features constructed in the previous iterations. During the synthesis phase, we use knowledge distillation to force the network to simultaneously develop all the features identified during the discovery phase. RFC consistently helps six OoD methods achieve top performance on challenging invariant training benchmarks, ColoredMNIST (Arjovsky et al., 2020). Furthermore, on the realistic Camelyon17 task, our method helps both OoD and ERM methods outperform earlier compatable results by at least $5\%$, reduce standard deviation by at least $4.1\%$, and makes hyperparameter tuning and model selection more reliable.
Algorithmic Bias and Data Bias: Understanding the Relation between Distributionally Robust Optimization and Data Curation
Jun 17, 2021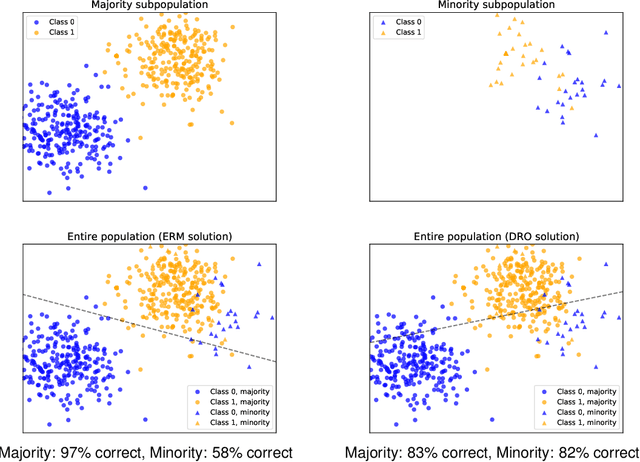
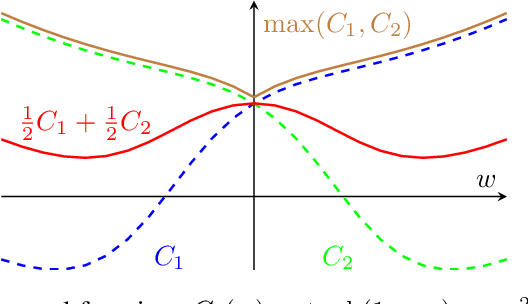
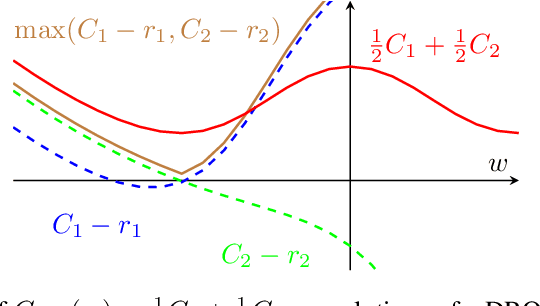
Abstract:Machine learning systems based on minimizing average error have been shown to perform inconsistently across notable subsets of the data, which is not exposed by a low average error for the entire dataset. In consequential social and economic applications, where data represent people, this can lead to discrimination of underrepresented gender and ethnic groups. Given the importance of bias mitigation in machine learning, the topic leads to contentious debates on how to ensure fairness in practice (data bias versus algorithmic bias). Distributionally Robust Optimization (DRO) seemingly addresses this problem by minimizing the worst expected risk across subpopulations. We establish theoretical results that clarify the relation between DRO and the optimization of the same loss averaged on an adequately weighted training dataset. The results cover finite and infinite number of training distributions, as well as convex and non-convex loss functions. We show that neither DRO nor curating the training set should be construed as a complete solution for bias mitigation: in the same way that there is no universally robust training set, there is no universal way to setup a DRO problem and ensure a socially acceptable set of results. We then leverage these insights to provide a mininal set of practical recommendations for addressing bias with DRO. Finally, we discuss ramifications of our results in other related applications of DRO, using an example of adversarial robustness. Our results show that there is merit to both the algorithm-focused and the data-focused side of the bias debate, as long as arguments in favor of these positions are precisely qualified and backed by relevant mathematics known today.
On the Convergence of Adam and Adagrad
Mar 05, 2020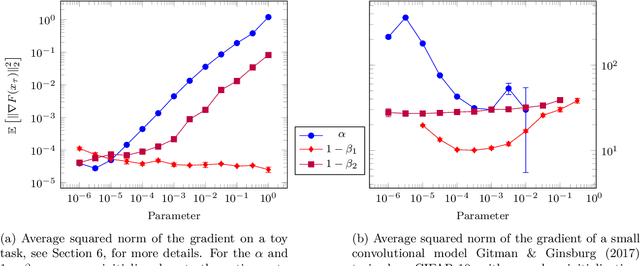
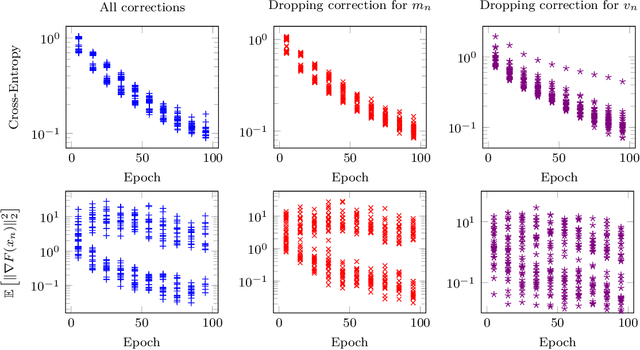
Abstract:We provide a simple proof of the convergence of the optimization algorithms Adam and Adagrad with the assumptions of smooth gradients and almost sure uniform bound on the $\ell_\infty$ norm of the gradients. This work builds on the techniques introduced by Ward et al. (2019) and extends them to the Adam optimizer. We show that in expectation, the squared norm of the objective gradient averaged over the trajectory has an upper-bound which is explicit in the constants of the problem, parameters of the optimizer and the total number of iterations N. This bound can be made arbitrarily small. In particular, Adam with a learning rate $\alpha=1/\sqrt{N}$ and a momentum parameter on squared gradients $\beta_2=1 - 1/N$ achieves the same rate of convergence $O(\ln(N)/\sqrt{N})$ as Adagrad. Thus, it is possible to use Adam as a finite horizon version of Adagrad, much like constant step size SGD can be used instead of its asymptotically converging decaying step size version.
Music Source Separation in the Waveform Domain
Nov 27, 2019



Abstract:Source separation for music is the task of isolating contributions, or stems, from different instruments recorded individually and arranged together to form a song. Such components include voice, bass, drums and any other accompaniments. Contrarily to many audio synthesis tasks where the best performances are achieved by models that directly generate the waveform, the state-of-the-art in source separation for music is to compute masks on the magnitude spectrum. In this paper, we first show that an adaptation of Conv-Tasnet (Luo \& Mesgarani, 2019), a waveform-to-waveform model for source separation for speech, significantly beats the state-of-the-art on the MusDB dataset, the standard benchmark of multi-instrument source separation. Second, we observe that Conv-Tasnet follows a masking approach on the input signal, which has the potential drawback of removing parts of the relevant source without the capacity to reconstruct it. We propose Demucs, a new waveform-to-waveform model, which has an architecture closer to models for audio generation with more capacity on the decoder. Experiments on the MusDB dataset show that Demucs beats previously reported results in terms of signal to distortion ratio (SDR), but lower than Conv-Tasnet. Human evaluations show that Demucs has significantly higher quality (as assessed by mean opinion score) than Conv-Tasnet, but slightly more contamination from other sources, which explains the difference in SDR. Additional experiments with a larger dataset suggest that the gap in SDR between Demucs and Conv-Tasnet shrinks, showing that our approach is promising.
Symplectic Recurrent Neural Networks
Sep 29, 2019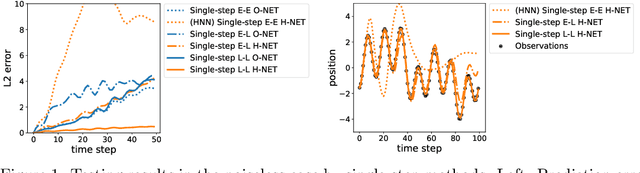
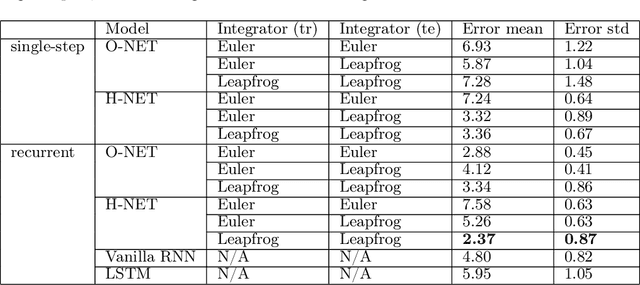
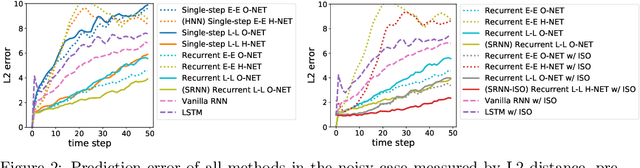
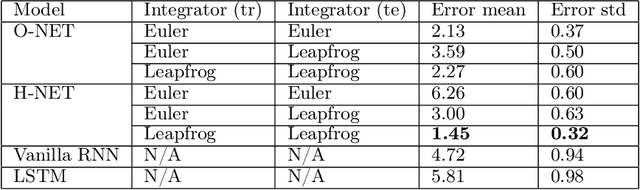
Abstract:We propose Symplectic Recurrent Neural Networks (SRNNs) as learning algorithms that capture the dynamics of physical systems from observed trajectories. An SRNN models the Hamiltonian function of the system by a neural network and furthermore leverages symplectic integration, multiple-step training and initial state optimization to address the challenging numerical issues associated with Hamiltonian systems. We show SRNNs succeed reliably on complex and noisy Hamiltonian systems. We also show how to augment the SRNN integration scheme in order to handle stiff dynamical systems such as bouncing billiards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge