Zhengdao Chen
On the Interpolation Effect of Score Smoothing
Feb 26, 2025Abstract:Score-based diffusion models have achieved remarkable progress in various domains with the ability to generate new data samples that do not exist in the training set. In this work, we examine the hypothesis that their generalization ability arises from an interpolation effect caused by a smoothing of the empirical score function. Focusing on settings where the training set lies uniformly in a one-dimensional linear subspace, we study the interplay between score smoothing and the denoising dynamics with mathematically solvable models. In particular, we demonstrate how a smoothed score function can lead to the generation of samples that interpolate among the training data within their subspace while avoiding full memorization. We also present evidence that learning score functions with regularized neural networks can have a similar effect on the denoising dynamics as score smoothing.
Neural Hilbert Ladders: Multi-Layer Neural Networks in Function Space
Jul 03, 2023


Abstract:The characterization of the functions spaces explored by neural networks (NNs) is an important aspect of deep learning theory. In this work, we view a multi-layer NN with arbitrary width as defining a particular hierarchy of reproducing kernel Hilbert spaces (RKHSs), named a Neural Hilbert Ladder (NHL). This allows us to define a function space and a complexity measure that generalize prior results for shallow NNs, and we then examine their theoretical properties and implications in several aspects. First, we prove a correspondence between functions expressed by L-layer NNs and those belonging to L-level NHLs. Second, we prove generalization guarantees for learning an NHL with the complexity measure controlled. Third, corresponding to the training of multi-layer NNs in the infinite-width mean-field limit, we derive an evolution of the NHL characterized as the dynamics of multiple random fields. Fourth, we show examples of depth separation in NHLs under ReLU and quadratic activation functions. Finally, we complement the theory with numerical results to illustrate the learning of RKHS in NN training.
A Non-Asymptotic Analysis of Oversmoothing in Graph Neural Networks
Dec 21, 2022



Abstract:A central challenge of building more powerful Graph Neural Networks (GNNs) is the oversmoothing phenomenon, where increasing the network depth leads to homogeneous node representations and thus worse classification performance. While previous works have only demonstrated that oversmoothing is inevitable when the number of graph convolutions tends to infinity, in this paper, we precisely characterize the mechanism behind the phenomenon via a non-asymptotic analysis. Specifically, we distinguish between two different effects when applying graph convolutions -- an undesirable mixing effect that homogenizes node representations in different classes, and a desirable denoising effect that homogenizes node representations in the same class. By quantifying these two effects on random graphs sampled from the Contextual Stochastic Block Model (CSBM), we show that oversmoothing happens once the mixing effect starts to dominate the denoising effect, and the number of layers required for this transition is $O(\log N/\log (\log N))$ for sufficiently dense graphs with $N$ nodes. We also extend our analysis to study the effects of Personalized PageRank (PPR) on oversmoothing. Our results suggest that while PPR mitigates oversmoothing at deeper layers, PPR-based architectures still achieve their best performance at a shallow depth and are outperformed by the graph convolution approach on certain graphs. Finally, we support our theoretical results with numerical experiments, which further suggest that the oversmoothing phenomenon observed in practice may be exacerbated by the difficulty of optimizing deep GNN models.
A Functional-Space Mean-Field Theory of Partially-Trained Three-Layer Neural Networks
Oct 28, 2022



Abstract:To understand the training dynamics of neural networks (NNs), prior studies have considered the infinite-width mean-field (MF) limit of two-layer NN, establishing theoretical guarantees of its convergence under gradient flow training as well as its approximation and generalization capabilities. In this work, we study the infinite-width limit of a type of three-layer NN model whose first layer is random and fixed. To define the limiting model rigorously, we generalize the MF theory of two-layer NNs by treating the neurons as belonging to functional spaces. Then, by writing the MF training dynamics as a kernel gradient flow with a time-varying kernel that remains positive-definite, we prove that its training loss in $L_2$ regression decays to zero at a linear rate. Furthermore, we define function spaces that include the solutions obtainable through the MF training dynamics and prove Rademacher complexity bounds for these spaces. Our theory accommodates different scaling choices of the model, resulting in two regimes of the MF limit that demonstrate distinctive behaviors while both exhibiting feature learning.
On Feature Learning in Neural Networks with Global Convergence Guarantees
Apr 22, 2022
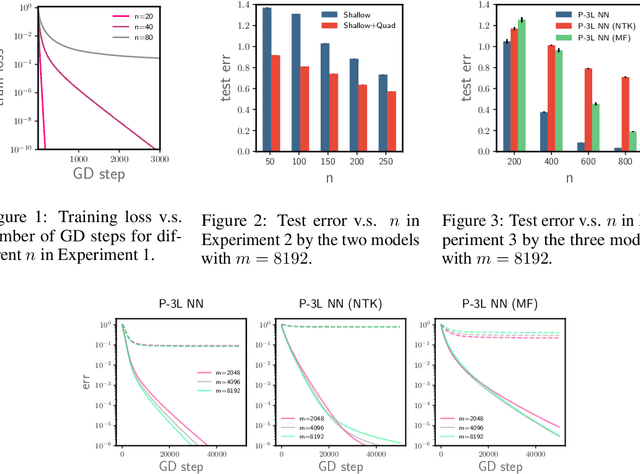
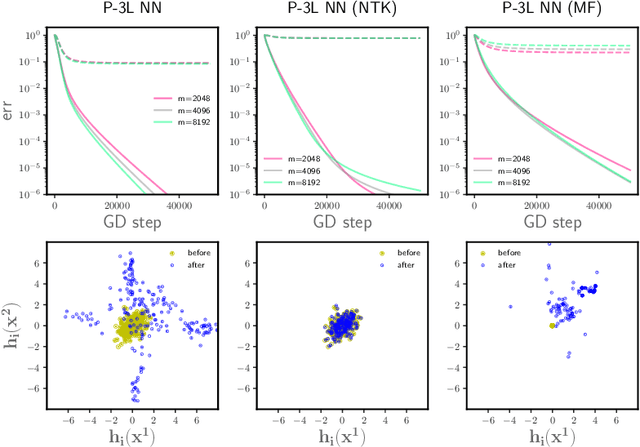
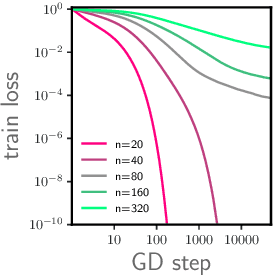
Abstract:We study the optimization of wide neural networks (NNs) via gradient flow (GF) in setups that allow feature learning while admitting non-asymptotic global convergence guarantees. First, for wide shallow NNs under the mean-field scaling and with a general class of activation functions, we prove that when the input dimension is no less than the size of the training set, the training loss converges to zero at a linear rate under GF. Building upon this analysis, we study a model of wide multi-layer NNs whose second-to-last layer is trained via GF, for which we also prove a linear-rate convergence of the training loss to zero, but regardless of the input dimension. We also show empirically that, unlike in the Neural Tangent Kernel (NTK) regime, our multi-layer model exhibits feature learning and can achieve better generalization performance than its NTK counterpart.
On Graph Neural Networks versus Graph-Augmented MLPs
Oct 28, 2020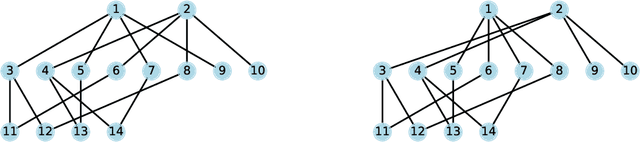
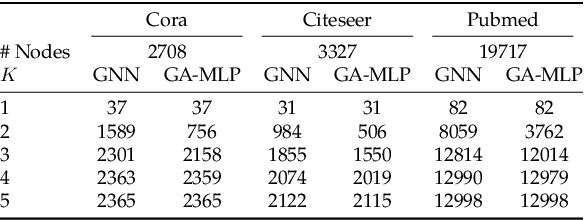
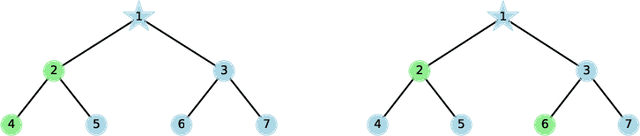
Abstract:From the perspective of expressive power, this work compares multi-layer Graph Neural Networks (GNNs) with a simplified alternative that we call Graph-Augmented Multi-Layer Perceptrons (GA-MLPs), which first augments node features with certain multi-hop operators on the graph and then applies an MLP in a node-wise fashion. From the perspective of graph isomorphism testing, we show both theoretically and numerically that GA-MLPs with suitable operators can distinguish almost all non-isomorphic graphs, just like the Weifeiler-Lehman (WL) test. However, by viewing them as node-level functions and examining the equivalence classes they induce on rooted graphs, we prove a separation in expressive power between GA-MLPs and GNNs that grows exponentially in depth. In particular, unlike GNNs, GA-MLPs are unable to count the number of attributed walks. We also demonstrate via community detection experiments that GA-MLPs can be limited by their choice of operator family, as compared to GNNs with higher flexibility in learning.
A Dynamical Central Limit Theorem for Shallow Neural Networks
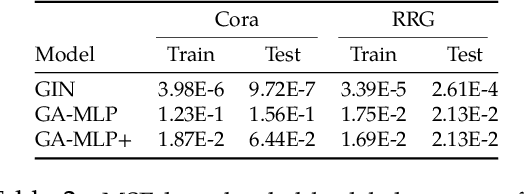
Aug 21, 2020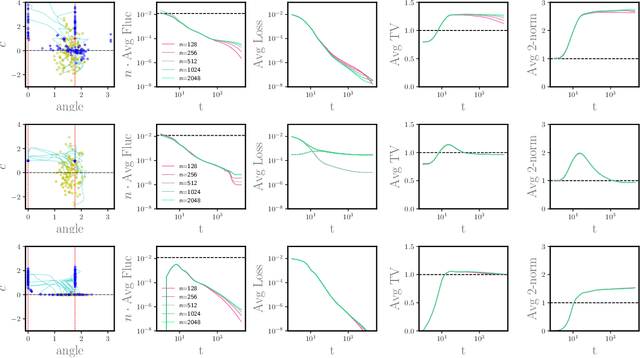

Abstract:Recent theoretical work has characterized the dynamics of wide shallow neural networks trained via gradient descent in an asymptotic regime called the mean-field limit as the number of parameters tends towards infinity. At initialization, the randomly sampled parameters lead to a deviation from the mean-field limit that is dictated by the classical Central Limit Theorem (CLT). However, the dynamics of training introduces correlations among the parameters, raising the question of how the fluctuations evolve during training. Here, we analyze the mean-field dynamics as a Wasserstein gradient flow and prove that the deviations from the mean-field limit scaled by the width, in the width-asymptotic limit, remain bounded throughout training. In particular, they eventually vanish in the CLT scaling if the mean-field dynamics converges to a measure that interpolates the training data. This observation has implications for both the approximation rate and the generalization: the upper bound we obtain is given by a Monte-Carlo type resampling error, which does not depend explicitly on the dimension. This bound motivates a regularizaton term on the 2-norm of the underlying measure, which is also connected to generalization via the variation-norm function spaces.
Can graph neural networks count substructures?
Feb 27, 2020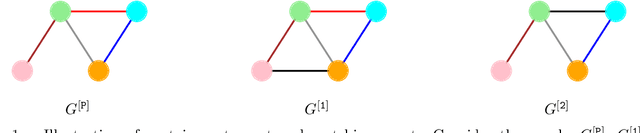
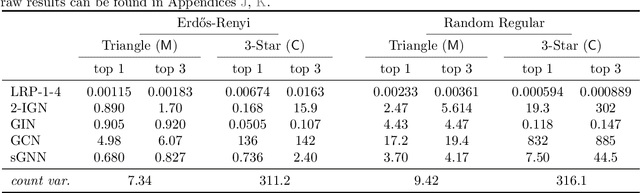

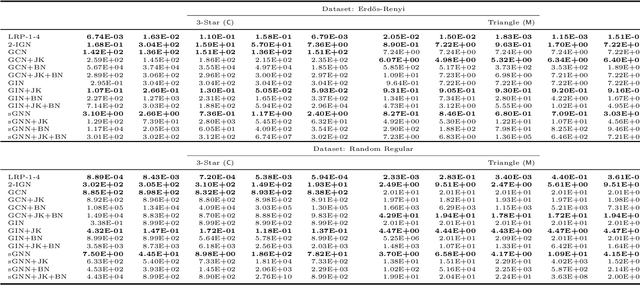
Abstract:The ability to detect and count certain substructures in graphs is important for solving many tasks on graph-structured data, especially in the contexts of computational chemistry and biology as well as social network analysis. Inspired by this, we propose to study the expressive power of graph neural networks (GNNs) via their ability to count attributed graph substructures, extending recent works that examine their power in graph isomorphism testing and function approximation. We distinguish between two types of substructure counting: matching-count and containment-count, and establish both positive and negative answers for popular GNN architectures. Specifically, we prove that Message Passing Neural Networks (MPNNs), 2-Weisfeiler-Lehman (2-WL) and 2-Invariant Graph Networks (2-IGNs) cannot perform matching-count of substructures consisting of 3 or more nodes, while they can perform containment-count of star-shaped substructures. We also prove positive results for k-WL and k-IGNs as well as negative results for k-WL with limited number of iterations. We then conduct experiments that support the theoretical results for MPNNs and 2-IGNs, and demonstrate that local relational pooling strategies inspired by Murphy et al. (2019) are more effective for substructure counting. In addition, as an intermediary step, we prove that 2-WL and 2-IGNs are equivalent in distinguishing non-isomorphic graphs, partly answering an open problem raised in Maron et al. (2019).
Symplectic Recurrent Neural Networks
Sep 29, 2019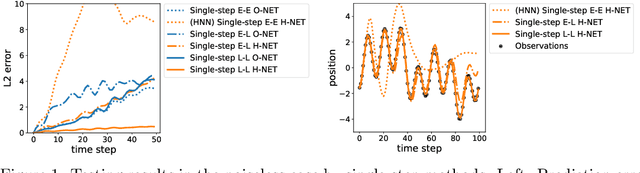
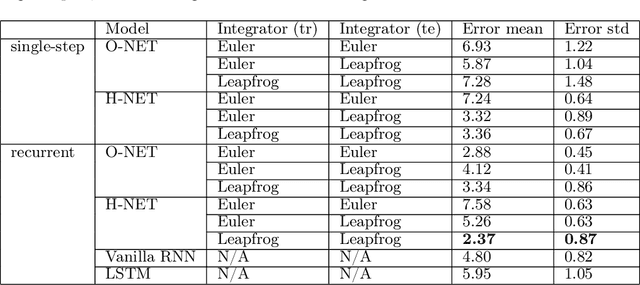
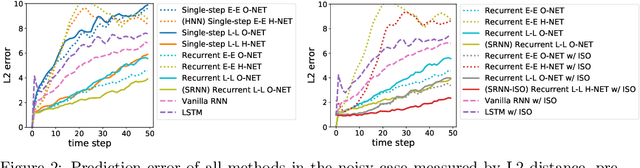
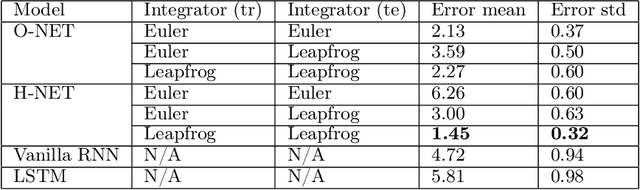
Abstract:We propose Symplectic Recurrent Neural Networks (SRNNs) as learning algorithms that capture the dynamics of physical systems from observed trajectories. An SRNN models the Hamiltonian function of the system by a neural network and furthermore leverages symplectic integration, multiple-step training and initial state optimization to address the challenging numerical issues associated with Hamiltonian systems. We show SRNNs succeed reliably on complex and noisy Hamiltonian systems. We also show how to augment the SRNN integration scheme in order to handle stiff dynamical systems such as bouncing billiards.
On the equivalence between graph isomorphism testing and function approximation with GNNs
May 29, 2019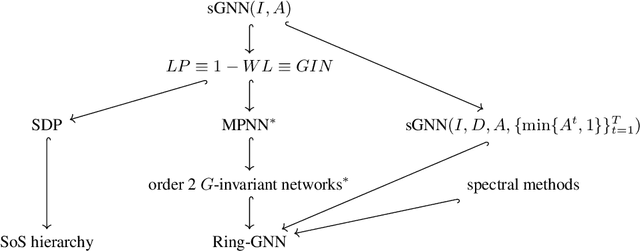
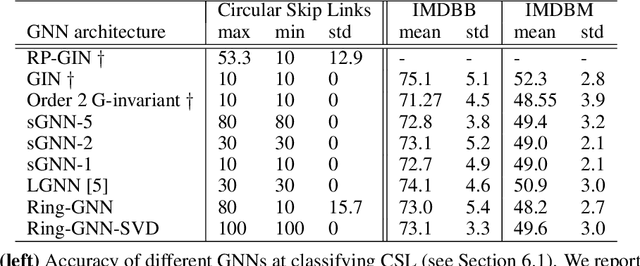
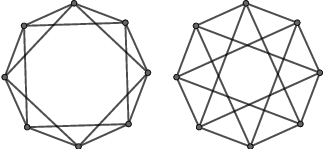
Abstract:Graph neural networks (GNNs) have achieved lots of success on graph-structured data. In the light of this, there has been increasing interest in studying their representation power. One line of work focuses on the universal approximation of permutation-invariant functions by certain classes of GNNs, and another demonstrates the limitation of GNNs via graph isomorphism tests. Our work connects these two perspectives and proves their equivalence. We further develop a framework of the representation power of GNNs with the language of sigma-algebra, which incorporates both viewpoints. Using this framework, we compare the expressive power of different classes of GNNs as well as other methods on graphs. In particular, we prove that order-2 Graph G-invariant networks fail to distinguish non-isomorphic regular graphs with the same degree. We then extend them to a new architecture, Ring-GNNs, which succeeds on distinguishing these graphs and provides improvements on real-world social network datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge